查找
查找
二分查找
public class BinarySearch<T extends Comparable<T>> {
private T[] arr;
public BinarySearch(T[] arr) {
this.arr = arr;
}
}
1. 等于:返回等于 key 的元素下标
public int searchEq(T key) {
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
int cmp = arr[m].compareTo(key);
if (cmp == 0) {
return m;
}
if (cmp < 0) {
l = m + 1;
} else {
r = m - 1;
}
}
return -1;
}
2. 小于:返回小于 key 的最大下标
public int searchLess(T key) {
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
int cmp = arr[m].compareTo(key);
if (cmp >= 0) {
// arr[m] >= key 所求一定在 m 左侧
r = m - 1;
} else {
l = m + 1;
}
}
return r;
}
3. 不大于:返回不大于 key 的最大下标
public int searchLessEq(T key) {
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
int cmp = arr[m].compareTo(key);
if (cmp > 0) {
// arr[m] > key 所求一定在 m 左侧
r = m - 1;
} else {
l = m + 1;
}
}
return r;
}
4. 大于:返回大于 key 的最小下标
public int searchMore(T key) {
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
int cmp = arr[m].compareTo(key);
if (cmp <= 0) {
// arr[m] <= key 所求一定在 m 右侧
l = m + 1;
} else {
r = m - 1;
}
}
return l;
}
5. 不小于:返回不小于 key 的最小下标
public int searchMoreEq(T key) {
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
int cmp = arr[m].compareTo(key);
if (cmp < 0) {
// arr[m] < key 所求一定在 m 右侧
l = m + 1;
} else {
r = m - 1;
}
}
return l;
}
规律
while (l <= r) {
int m = l + ((r - l) >> 1);
int cmp = arr[m].compareTo(key);
if (cmp ? 0) { // [1]
??? // [2]
} else {
??? // [3]
}
}
return ?; // [4]
[1][2] 是必然性的推断。比如寻找不大于 key 的最大下标:如果arr[m] > key,那么结果必然是在 m 的左侧,即可得到cmp > 0; r = m - 1;
[3] 与[2]相反。
[4] 因为循环结束的条件是l > r所以最后l是在r的右侧。当[2]中推断在左侧时,返回r;推断在右侧时,返回l。
注:循环条件是l <= r而不是l < r。假设只有一个元素:直接跳过循环,这样显然是错误的。
二叉查找树
或称二叉排序树,二叉搜索树。与二分查找类似,都是同样的思想。
BST 是一颗二叉树,每个结点:
- 左子树上所有结点的值均 小于 该结点的值
- 右子树上所有结点的值均 大于 该结点的值
因此,中序遍历 BST 得到递增数列。
同样,判断一棵二叉树是否为 BST:中序遍历结果是否递增有序。
public class BST<T extends Comparable<T>> {
private Node root;
public int size() {
return root.num;
}
public Node get(T val) {
return get(root, val);
}
private Node get(Node node, T val) {
if (node == null)
return null;
int cmp = val.compareTo(node.val);
if (cmp == 0) {
return node;
}
if (cmp < 0) {
return get(node.left, val);
} else {
return get(node.right, val);
}
}
public void add(T val) {
root = add(root, val);
}
private Node add(Node node, T val) {
if (node == null)
return new Node(val, 1);
int cmp = val.compareTo(node.val);
if (cmp == 0) {
return node;
}
if (cmp < 0) {
node.left = add(node.left, val);
} else {
node.right = add(node.right, val);
}
recalculateSize(node);
return node;
}
public void delete(T val) {
root = delete(root, val);
}
private Node delete(Node node, T val) {
if (node == null)
return null;
int cmp = val.compareTo(node.val);
if (cmp < 0) {
node.left = delete(node.left, val);
} else if (cmp > 0) {
node.right = delete(node.right, val);
} else {
if (node.right == null)
return node.left;
if (node.left == null)
return node.right;
Node t = node;
node = min(t.right);
node.right = deleteMin(t.right);
node.left = t.left;
}
recalculateSize(node);
return node;
}
public T min() {
return min(root).val;
}
private Node min(Node x) {
if (x == null)
return null;
if (x.left == null)
return x;
return min(x.left);
}
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node node) {
if (node.left == null)
return node.right;
node.left = deleteMin(node.left);
recalculateSize(node);
return node;
}
public List<T> keys() {
List<T> list = new ArrayList<>();
keys(root, list);
return list;
}
private void keys(Node node, List<T> list) {
if (node == null)
return;
keys(node.left, list);
list.add(node.val);
keys(node.right, list);
}
public int rank(T val) {
return rank(val, root);
}
private int rank(T val, Node x) {
if (x == null)
return 0;
int cmp = val.compareTo(x.val);
if (cmp == 0) {
return size(x.left);
}
if (cmp < 0) {
return rank(val, x.left);
} else {
return 1 + size(x.left) + rank(val, x.right);
}
}
private int size(Node node) {
if (node == null)
return 0;
return node.num;
}
private void recalculateSize(Node node) {
node.num = size(node.left) + size(node.right) + 1;
}
class Node {
Node left;
Node right;
T val;
int num; // 以该结点为根的子树结点总数
Node(T val, int num) {
this.val = val;
this.num = num;
}
}
}
平衡二叉树
AVL 是 BST,且满足:
- 左、右子树都是平衡二叉树
- 左、右子树高度之差的绝对值不超过 1
public class AVL<T extends Comparable<T>> {
protected Node root;
class Node {
Node left;
Node right;
T val;
int height;
boolean color;
Node(T val) {
this.val = val;
this.height = 1;
}
}
public T max() {
return max(root);
}
public T min() {
return min(root);
}
private T max(Node node) {
if (node == null)
return null;
while (node.right != null)
node = node.right;
return node.val;
}
private T min(Node node) {
if (node == null)
return null;
while (node.left != null)
node = node.left;
return node.val;
}
public void add(T val) {
root = add(root, val);
}
private Node add(Node node, T val) {
if (node == null)
return new Node(val);
int cmp = val.compareTo(node.val);
if (cmp == 0) {
return node;
}
if (cmp < 0) {
node.left = add(node.left, val);
} else {
node.right = add(node.right, val);
}
node = balance(node);
return node;
}
public void delete(T val) {
root = delete(root, val);
}
private Node delete(Node node, T val) {
if (node == null)
return null;
int cmp = val.compareTo(node.val);
if (cmp == 0) {
if (node.left == null || node.right == null) {
// 至少一个孩子结点为空
node = node.left == null ? node.right : node.left;
} else {
// 左右子结点均不为空
if (height(node.left) > height(node.right)) {
// 左边高 则取左子树最大结点替代该结点 再删除最大结点
T tmp = max(node.left);
node.val = tmp;
node.left = delete(node.left, tmp);
} else {
// 否则 取右子树最小结点替代该结点 再删除最小结点
T tmp = min(node.right);
node.val = tmp;
node.right = delete(node.right, tmp);
}
}
} else if (cmp < 0) {
node.left = delete(node.left, val);
} else {
node.right = delete(node.right, val);
}
node = balance(node);
return node;
}
private Node balance(Node node) {
if (node == null)
return node;
int diff = height(node.left) - height(node.right);
if (diff > 1) {
if (height(node.left.left) > height(node.left.right)) {
// LL 型 单向右旋
node = llRotate(node);
} else {
// LR 型 先左孩子左旋 再右旋
node = lrRotate(node);
}
} else if (diff < -1) {
if (height(node.right.left) < height(node.right.right)) {
// RR 型 单向左旋
node = rrRotate(node);
} else {
// RL 型 先右孩子右旋 再左旋
node = rlRotate(node);
}
} else {
updateHeight(node);
}
return node;
}
// 单向右旋 该结点变为左孩子的右结点
protected Node llRotate(Node node) {
Node tmp = node.left;
node.left = tmp.right;
tmp.right = node;
updateHeight(node);
tmp.height = Math.max(node.height, height(tmp.left)) + 1;
return tmp;
}
// 单向左旋 该结点变为右孩子的左结点
protected Node rrRotate(Node node) {
Node tmp = node.right;
node.right = tmp.left;
tmp.left = node;
updateHeight(node);
tmp.height = Math.max(node.height, height(tmp.right)) + 1;
return tmp;
}
// 先左孩子左旋 该结点再右旋
private Node lrRotate(Node node) {
node.left = rrRotate(node.left);
return llRotate(node);
}
// 先右孩子右旋 该结点再左旋
private Node rlRotate(Node node) {
node.right = llRotate(node.right);
return rrRotate(node);
}
protected void updateHeight(Node node) {
node.height = Math.max(height(node.left), height(node.right)) + 1;
}
private int height(Node node) {
if (node == null)
return 0;
return node.height;
}
public void traverse(String msg) {
System.out.println("==== " + msg + " ====");
if (root == null)
return;
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while (queue.size() > 0) {
int num = queue.size();
for (int i = 0; i < num; i++) {
Node node = queue.poll();
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
System.out.println("val:" + node.val + " " + "height:" + node.height);
}
}
System.out.println();
}
public static void main(String[] args) {
AVL<Integer> avl = new AVL<>();
List<Integer> list = new ArrayList<>();
for (int i = 1; i <= 9; i++) {
list.add(i);
}
Collections.shuffle(list);
for (int i : list) {
avl.add(i);
avl.traverse("add " + i);
}
Collections.shuffle(list);
for (int i : list) {
avl.delete(i);
avl.traverse("del " + i);
}
}
}
AVL 实现平衡的关键在于旋转。旋转操作是对 最小的不平衡子树 进行的。
- LL 型:将 A 右旋,变为左孩子 B 的右结点
A
/
B
/
C
- RR 型:将 A 左旋,变为右孩子 B 的左结点
A
\
B
\
C
- LR 型:将左孩子 B 左旋 再将 A 右旋
A
/
B
\
C
- RL 型:将右孩子 B 右旋 再将 A 左旋
A
\
B
/
C
深度为 \(h\) 的二叉平衡树最少结点数 \(N_h = N_{h-1} + N_{h-2} + 1 = F(h + 2) - 1 \qquad F 为斐波那契数列\)
B 树
B-tree,即 B- 树,是一种 平衡的多路查找树。
m 阶 B-tree 是满足下列特性的 m 叉树:
- 每个结点最多 m 棵子树
- 根结点有 0 或 >= 2 棵子树(不能只有 1 棵子树)
- 其他非叶结点有 >= $ \lceil m/2 \rceil $ 棵子树(一半以上)
- 所有的非叶结点包含:
- n 个递增的关键字
- n + 1 个子树指针,子树的关键字范围被 n 个关键字划分开
- 所有叶子结点位于同一层,为 null
2-3 树
3 阶 B-tree 又名 2-3 树,每个非叶结点最少 2 棵子树,最多 3 棵子树。
插入 :
- 插入到 2- 结点:直接变为 3- 结点
- 插入到 3- 结点:将该结点分裂为 3 个 2- 结点,并将中间结点上移,以此类推。
红黑树
红黑树可以理解为 2-3 树,但红黑树的每个结点只含一个关键字(2- 结点),形为普通二叉搜索树,通过额外添加一个颜色属性,来标志 2- 结点或 3- 结点。
- 红结点: 父结点指向该结点的(左)链接为红链接,红结点与父结点一起构成一个 3- 结点
- 黑结点:普通的 2- 结点
如果将红色链接放平,就可以看作为一棵 2-3 树。
红黑树
b 黑结点
红链接- / \
a 红结点
/ \
a - b 红链接放平
/ \ \
2-3 树
a b 3- 结点
/ | \
由此,红黑树是一棵二叉查找树,且:
- 根结点和叶子结点(null)是黑结点
- 红链接均为左链接
- 不存在同时连接两条红链接的结点
- 完美黑色平衡 :从任一点到其叶子结点的简单路径上黑结点数相同
从根结点到叶子结点的最短路径上全为黑结点,个数为 \(n\),路径长度 \(n-1\)。
从根结点到叶子结点的最长路径上红黑结点相间,两端为黑结点,红结点个数为 \(n - 1\),总结点数 \(2n-1\),路径长度 \(2n-2\),为最短路径的 2 倍。
一棵 \(N\) 个结点的红黑树高度不超过 \(2log(N+1)\)。
平衡
红黑树实现黑色平衡的方式同样是旋转,相比普通的平衡二叉树,旋转操作多了对颜色的处理。
红黑树插入过程中结点可能的状态有以下几种:
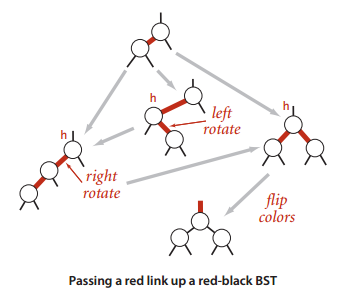
最上和最下是正确的状态,中间三种是错误的状态,对应三种修正方法:
- 左旋:存在右红链接
- 右旋:存在连续两条左红链接
- 反转:存在左右链接均为红色
public class RedBlackTree<T extends Comparable<T>> extends AVL<T> {
private static final boolean RED = false;
private static final boolean BLACK = true;
private boolean isRed(Node node) {
return node != null && node.color == RED;
}
@Override
public void add(T val) {
root = add(root, val);
root.color = BLACK;
}
private Node add(Node node, T val) {
if (node == null)
return new Node(val); // 新结点默认为红
int cmp = val.compareTo(node.val);
if (cmp < 0) {
node.left = add(node.left, val);
} else if (cmp > 0) {
node.right = add(node.right, val);
}
// 这里的修正不能使用 else if
// 因为即使修正之后 也可能转换成另外一种错误情况
// 右侧红链接 左旋修正
if (!isRed(node.left) && isRed(node.right)) {
node = leftRotate(node);
}
// 连续红链接 右旋修正
if (isRed(node.left) && isRed(node.left.left)) {
node = rightRotate(node);
}
// 左右红链接 反转修正
if (isRed(node.left) && isRed(node.right))
flipColor(node);
updateHeight(node);
return node;
}
private Node leftRotate(Node node) {
Node tmp = node.right;
tmp.color = node.color;
node.color = RED;
node = rrRotate(node);
return node;
}
private Node rightRotate(Node node) {
Node tmp = node.left;
tmp.color = node.color;
node.color = RED;
node = llRotate(node);
return node;
}
private void flipColor(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
}
B+ 树
B+ 树与 B 树类似,区别在于:
- 非叶结点关键字与子树个数相同
- 所有关键字都在叶子结点中出现
- 所有叶子结点被顺次连接起来
散列表
散列表类似于数组,可以把散列表的散列值看成数组的索引值,插入和查找操作都在常数时间内完成。
但散列后的结果不能保证有序,所以散列表是无序的。
散列函数
对于一个大小为 M 的散列表,散列函数能够把任意键转换为 [0, M-1] 内的正整数,该正整数即为 hash 值。
散列函数应该满足以下三个条件:
- 一致性:相等的键应当有相等的 hash 值,两个键相等表示调用 equals() 返回的值相等。
- 高效性:计算应当简便,有必要的话可以把 hash 值缓存起来,在调用 hash 函数时直接返回。
- 均匀性:所有键的 hash 值应当均匀地分布到 [0, M-1] 之间,如果不能满足这个条件,有可能产生很多冲突,从而导致散列表的性能下降。
常用方法: 除留余数法。设定哈希函数为: \(h(key) = key MOD p\)
其他方法:
- 直接定址法:哈希函数为关键字的线性函数。如:\(h(key)= key\) 或者 \(h(key)=a×key+b\)
- 数字分析法:假设每个 key 都是由 s 位数字组成,分析 key 集合, 从中提取分布均匀的若干位或它们的组合作为地址。
- 平方取中法:以 key 的平方值的中间几位作为存储地址。
- 折叠法:将 key 分成位数相等的几部分,然后将这几部分叠加求和作为哈希地址。
- 随机数法:$ h(key) = Random(key)$ 其中,Random 为伪随机函数。
说明:若是非数字关键字,则需先对其进行数字化处理。
解决冲突
- 开放定址法:设定一个地址探测序列\(h_i = (h(key) + d_i ) MOD m\)
- 线性探测 : \(d_i = i\)
- 平方探测 : \(d_i = 1^2 , -1^2 , 2^2 , -2^2...\)
- 随机探测 : \(d_i\) 是一组伪随机数列
- 再哈希法:为冲突地址再次散列
- 链地址法:使用链表存储冲突的键值
- 建立一个公共溢出区:将发生冲突的数据元素顺序存放于一个公共的溢出区



 浙公网安备 33010602011771号
浙公网安备 33010602011771号