【POJ1006】Biorhythms——中国剩余定理
题目大意:
人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天。一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期。然后再给出一个起始日期,要求从这一天开始,算出最少再过多少天后三个峰值同时出现。
分析:
首先有必要知道一下中国剩余定理:
对于两两互质的数m1,m2...mi,要求一个最小的x使得满足
x%m1=a1;
x%m2=a2;
......
x%mi=ai。
那么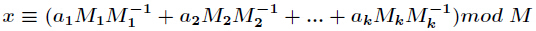
其中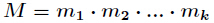
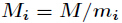
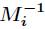 为
为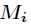 模
模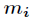 的逆元。
的逆元。
第一个样例已经告诉我们周期为21252,因此如果算出来的day<d,那么说明至少还要再经过k个周期使得day+k>=d。
接下来就是各种细节要处理好,答案是day-d,求逆元用的是扩展欧几里德算法。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 typedef long long LL; 5 using namespace std; 6 int k[4],m[4],M=23*28*33; 7 int read() 8 { 9 int ans=0,f=1;char c=getchar(); 10 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} 11 while(c>='0'&&c<='9'){ans=ans*10+c-48;c=getchar();} 12 return ans*f; 13 } 14 void ex_gcd(int a,int b,int& x,int& y) 15 { 16 if(b==0){ 17 x=1; 18 y=0; 19 return; 20 } 21 ex_gcd(b,a%b,x,y); 22 int t=x; 23 x=y; 24 y=t-a/b*y; 25 } 26 int China(int k[],int m[]) 27 { 28 int x,y,ans=0; 29 for(int i=1;i<=3;i++){ 30 int t=M/m[i]; 31 ex_gcd(t,m[i],x,y); 32 ans=(ans+k[i]*x*t)%M; 33 } 34 if(ans<0)ans+=M; 35 return ans; 36 } 37 int main() 38 { 39 int a,b,c,d,sum=0;m[1]=23;m[2]=28;m[3]=33; 40 a=read();b=read();c=read();d=read(); 41 while(a!=-1){ 42 k[1]=a;k[2]=b;k[3]=c; 43 int day=China(k,m); 44 while(day<=d)day+=21252; 45 printf("Case %d: the next triple peak occurs in %d days.\n",++sum,day-d); 46 a=read();b=read();c=read();d=read(); 47 } 48 return 0; 49 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号