数学篇 cad.net 入门数学 向量+点乘+叉乘+矩阵+三维旋转+凸度+反三角函数+导数应用+求余
数学学得好的,都是能把人家的描述语言变成自己的描述语言.
例如你叫这个"矢量积"我叫它"叉积"(叉烧+鸡),当你熟悉了之后,再统一回来,你会发现心情宽阔.
向量(轴)
在编程上面,向量用(X,Y,Z)表示,也就是(123.156,194.156,215,00)
它和点的数据结构是一样的,主要的目的是累加方向和计算夹角.
为什么有向量呢?
因为用点描述一个操作的时候,往往需要进行两个点+平移.
例如"求夹角",没有向量的做法是将line的pt1,pt2其中一个点以另一个点平移到line2其中一个点,再进行勾股定理求解.
数学家们想,这样麻烦死了,不如它们都平移到(0,0,0),再进行xxxx...
记住一个原则就行:它表示原点(0,0,0)到(X,Y,Z)的方向和长度.
那么两个点怎么转换成向量呢？
数学上就是b点-a点==(x2-x1,y2-y1,z2-z1),而cad提供了一个方法pta.GetVectorTo(ptb)
而单位向量是什么?
我们知道了向量的方向性和大小性,但是方向一样时候大小可能不一样.
那我们怎么判断大小不一样的时候,方向是不是一样呢?
这个操作就是"归一化",也叫单位化.(它可以用来判断两根线是不是重叠)
cad是GetNormal,但是我用数学实现了一下,
看下面点乘中的 public static Point3d GetUnitNormal(this Point3d ob_vector) 了解得知 😃
而法向量是什么?
X轴Y轴形成的平面(XOY面)的法向量就是Z轴.
这有一个非常好的条件,知道一个面(两向量)可以求一个法向量,知道一个轴可以求轴的面(虽然有无限个).
知道面又有什么用呢？平面切割之后投影可见物啊!
还有的人喜欢把向量和点用标记区分:(x,y,z,标记)
那么他们运算是竖式计算:
(1,2,3,1) 点
+(4,5,6,0) 向量
---------------
=(5,7,9,1) 点
我撸了一个PointV类更好的说明了4个数字表达的优美,其中涉及了后续的矩阵齐次坐标等操作.
但是这只是个方法收集类,更优美的实现是SOA改为AOS,这方面需要考虑内存布局和CPU缓存机制,可以自行搜索.
点乘的意义
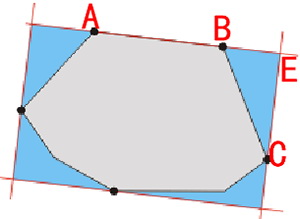
下图所示,通过向量OA,向量OB,求OP的距离和P点坐标.
现象就是A点投影到OB向量,呈现一个90度直角和P点,而且OA是任意角度的,不需要和x轴重合.
虽然说B站有视频教程,但是直接看代码貌似更方便理解.
再深入,通过A,B,C求E点,就是 E == (AC点乘AB).至于为什么要算E点,可以看 数学篇 cad.net 葛立恒凸包算法和面积最小包围盒.
测试命令:
/// <summary>
/// 测试点乘代码,点1=o,点2=a,点3=b
/// </summary>
[CommandMethod("CmdTest_DotProductOrCross")]
public void CmdTest_DotProductOrCross()
{
var dm = Acap.DocumentManager;
var ed = dm.MdiActiveDocument.Editor;
var ppo = new PromptPointOptions("");
var pts = new List<Point3d>();
for (int i = 0; i < 3; i++)
{
ppo.Message = $"{Environment.NewLine}点位置{i}:";
var pot = ed.GetPoint(ppo);
if (pot.Status != PromptStatus.OK)
return;
pts.Add(pot.Value);
}
var pickPoint = MathHelper.DotProduct(pts[0], pts[1], pts[2]);
ed.WriteMessage($"{Environment.NewLine}点乘P点是:" + pickPoint);
var pickLength = MathHelper.DotProductLength(pts[0], pts[1], pts[2]);
ed.WriteMessage($"{Environment.NewLine}点乘OP长度是:" + pickLength);
var ve1 = new Vector3d(1, 3, 4);
var ve2 = new Vector3d(2, 5, 9);
var ss1 = MathHelper.CrossNormal(ve1, ve2);
ed.WriteMessage($"{Environment.NewLine}叉乘测试****法向量是:" + ss1); //(7,-1,-1)
var aa = MathHelper.CrossAclockwise(pts[0], pts[1], pts[2]);
ed.WriteMessage($"{Environment.NewLine}叉乘测试*****逆时针:" + aa.ToString());
}
点积函数:
/// <summary>
/// 点积,求坐标
/// </summary>
/// <param name="o">原点</param>
/// <param name="a">点</param>
/// <param name="b">点</param>
/// <returns>坐标点</returns>
public static Point3d DotProduct(Point3d o, Point3d a, Point3d b)
{
//点乘就是将oa向量投射到ob向量上面,求得op坐标(也就是呈现90度角的坐标)
var oa = o.GetVectorTo(a);
var obUnit = o.GetVectorTo(b).GetUnitNormal();
var dot = (oa.X * obUnit.X) + (oa.Y * obUnit.Y) + (oa.Z * obUnit.Z);
var p = obUnit * dot;
//如果O不在坐标原点,则需要平移
return new Point3d(p.X + o.X, p.Y + o.Y, p.Z + o.Z);
}
/// <summary>
/// 点积,求值
/// <a href="https://zhuanlan.zhihu.com/p/359975221"> 1.是两个向量的长度与它们夹角余弦的积 </a>
/// <a href="https://www.cnblogs.com/JJBox/p/14062009.html#_label1"> 2.求四个点是否矩形使用 </a>
/// </summary>
/// <param name="o">原点</param>
/// <param name="a">点</param>
/// <param name="b">点</param>
/// <returns><![CDATA[>0方向相同,夹角0~90度;=0相互垂直;<0方向相反,夹角90~180度]]></returns>
public double DotProductValue(Point3d o, Point3d a, Point3d b)
{
var oa = o.GetVectorTo(a);
var ob = o.GetVectorTo(b);
return (oa._X * ob._X) + (oa._Y * ob._Y) + (oa._Z * ob._Z);
}
/// <summary>
/// 点积,求长度
/// </summary>
/// <param name="o">原点</param>
/// <param name="a">点</param>
/// <param name="b">点</param>
/// <returns>长度</returns>
public static double DotProductLength(Point3d o, Point3d a, Point3d b)
{
var p = DotProduct(o, a, b);
return o.GetDistanceTo(p);
}
/// <summary>
/// 获取单位向量,仿照向量的GetNormal的数学实现,了解原理,用了Point3d代替向量
/// </summary>
/// <param name="ob_vector"></param>
/// <returns></returns>
//https://www.bilibili.com/video/BV1qb411M7wL?from=search&seid=9280697047969917119
public static Point3d GetUnitNormal(this Point3d ob_vector)
{
#if true2
var ob_length = Point3d.Origin.GetDistanceTo(ob_vector);
return ob_vector / ob_length;
#else
//两点的距离,向量模长数学版 √(x²+y²+z²)
var ob_length = Math.Sqrt(ob_vector.X * ob_vector.X +
ob_vector.Y * ob_vector.Y +
ob_vector.Z * ob_vector.Z);
return new Point3d(ob_vector.X / ob_length, ob_vector.Y / ob_length, ob_vector.Z / ob_length)
#endif
}
叉乘的意义
叉乘有三个意义!
二维叉乘求面积:
A:返回值是数值,有正负,表示绕原点四象限的位置变换,也就是有向面积,面积属性可用来求解凸包的单峰函数.
见图理解一下交叉相乘求面积的数学知识(就是交叉相乘再相减),下方所有Cross函数也是基于此制作.
求平行四边形面积本来就是底乘以高只是换成坐标的求解方式,也可以参考知乎
代码同下.
二维叉乘求方向:
B:返回值是数值,有正负,如果>0就是逆时针.
/// <summary>
/// 叉积,二维叉乘计算
/// </summary>
/// <param name="a">传参是向量,表示原点是0,0</param>
/// <param name="b">传参是向量,表示原点是0,0</param>
/// <returns>其模为a与b构成的平行四边形面积</returns>
public static double Cross(Vector2d a, Vector2d b)
{
return a.X * b.Y - a.Y * b.X;
}
/// <summary>
/// 叉积,二维叉乘计算
/// </summary>
/// <param name="o">原点</param>
/// <param name="a">oa向量</param>
/// <param name="b">ob向量,此为判断点</param>
/// <returns>返回值有正负,表示绕原点四象限的位置变换,也就是有向面积</returns>
public static double Cross(Point2d o, Point2d a, Point2d b)
{
return Cross(o.GetVectorTo(a),o.GetVectorTo(b));
}
/// <summary>
/// 叉积,逆时针方向为真
/// </summary>
/// <param name="o">直线点1</param>
/// <param name="a">直线点2</param>
/// <param name="b">判断点</param>
/// <returns>b点在oa的逆时针<see cref="true"/></returns>
public static bool CrossAclockwise(Point2d o, Point2d a, Point2d b)
{
return Cross(o, a, b) > -1e-6;//浮点数容差考虑
}
三维叉乘:
C:返回值是向量.例如(X轴叉乘Y轴==Z轴),如果叉乘的不是XY轴,而是两个三维向量(并不需要90度),那么就可以求出一个平面的法向量.
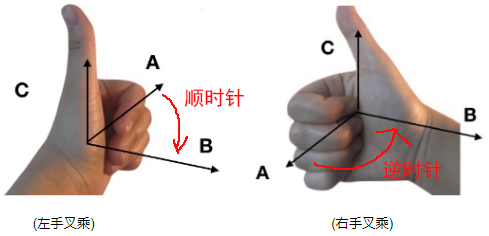
同样叫做A叉乘B,左右手叉乘的方式刚好方向相反.图来自,必要的视频参考
左右手坐标系相互转换:
如果将左a重合到右a,将左b重合到右b,那么左c和右c的关系刚好是正负的关系,结果*-1即可将左c变成右c.
(说明这个仅仅是为了,镜像导致cad图元的210组码(normal)为负数而做出关联修改方式)
三维叉乘(X轴*Y轴==Z轴)
/// <summary>
/// 叉积,求法向量
/// </summary>
/// <param name="a">向量a</param>
/// <param name="b">向量b</param>
/// <returns>右手坐标系系法向量</returns>
public static Vector3d CrossNormal(Vector3d a, Vector3d b)
{
//叉乘:依次用手指盖住每列,交叉相乘再相减,注意主副顺序
//(a.X a.Y a.Z)
//(b.X b.Y b.Z)
return new Vector3d(a.Y * b.Z - b.Y * a.Z, //主-副(左上到右下是主,左下到右上是副)
a.Z * b.X - b.Z * a.X, //副-主
a.X * b.Y - b.X * a.Y); //主-副
}
矩阵乘法
首先要学习一下矩阵乘法,主要掌握相乘再相加.
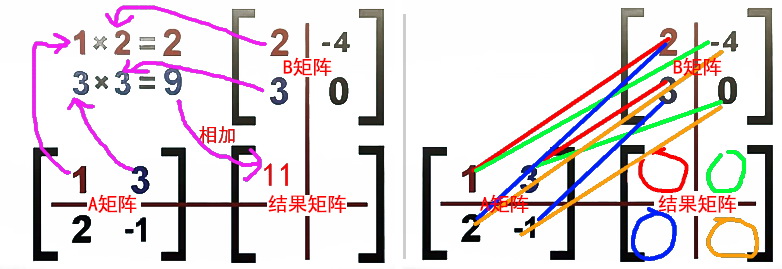
但是编程应用在于调用方法,只需要了解:
构造一个 xx(平移/旋转/缩放/透视..)矩阵 * 点 == 变换后的点.
齐次坐标
由于向量乘法需要满足a矩阵行和b矩阵列个数相同才能进行矩阵乘法,所以需要引入齐次坐标.
假设使用2x2的矩阵,是没有办法描述平移操作的,只有引入3x3矩阵形式,才能统一描述二维中的平移、旋转、缩放操作. 同理必须使用4x4的矩阵才能统一描述三维的变换.
若不然则可尝试将平移矩阵的结尾1去掉,你会发现不满足矩阵乘法了.
平移矩阵
二维
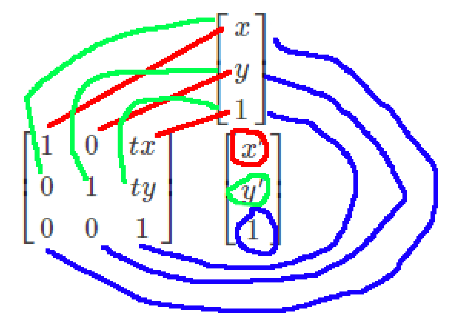
三维(一般用我)
透视矩阵
这里还有一个好玩的透视矩阵
旋转矩阵
有了矩阵乘法的思想了,所以应该去看看一些人家写好的方法了,我这里就没必要重复叙述了,
他写得太好了: 旋转矩阵
然后就可以去随便找一个c#矩阵代码,或者使用math.net库,抄一下跑一下,懂得原理后再抄代码心里舒服多啦
此处代码是我做的PointV类中使用到的.
public partial class Transform
{
/// <summary>
/// 旋转矩阵
/// </summary>
/// <param name="angle">角度</param>
/// <param name="axis">任意旋转轴</param>
/// <returns></returns>
public static Matrix GetRotateTransform(double angle, PointV axis)
{
angle = -angle;//保证是逆时针
var cos = Math.Cos(angle);
var sin = Math.Sin(angle);
var cosMinus = 1 - cos;
axis = axis.GetUnitNormal();
var u = axis.X;
var v = axis.Y;
var w = axis.Z;
var pOut = new double[4, 4];
{
pOut[0, 0] = cos + u * u * cosMinus;
pOut[0, 1] = u * v * cosMinus + w * sin;
pOut[0, 2] = u * w * cosMinus - v * sin;
pOut[0, 3] = 0;
pOut[1, 0] = u * v * cosMinus - w * sin;
pOut[1, 1] = cos + v * v * cosMinus;
pOut[1, 2] = w * v * cosMinus + u * sin;
pOut[1, 3] = 0;
pOut[2, 0] = u * w * cosMinus + v * sin;
pOut[2, 1] = v * w * cosMinus - u * sin;
pOut[2, 2] = cos + w * w * cosMinus;
pOut[2, 3] = 0;
pOut[3, 0] = 0;
pOut[3, 1] = 0;
pOut[3, 2] = 0;
pOut[3, 3] = 1;
}
return new Matrix(pOut);
}
/// <summary>
/// 应用旋转矩阵
/// </summary>
/// <param name="pts">点集</param>
/// <param name="rotateMat">旋转矩阵</param>
/// <returns></returns>
public static PointV[] WarpRotate(PointV[] pts, Matrix rotateMat)
{
#if DEBUG
if (rotateMat.Rows != rotateMat.Cols || rotateMat.Cols != 4)
throw new ArgumentNullException("WarpRotate矩阵大小不对");
#endif
var outPts = new List<PointV>();
foreach (var ptItem in pts)
outPts.Add(SetRotateMat(ptItem, rotateMat));
return outPts.ToArray();
}
/// <summary>
/// 应用旋转矩阵
/// </summary>
/// <param name="ptItem">点</param>
/// <param name="rotateMat">旋转矩阵</param>
/// <returns></returns>
public static PointV WarpRotate(PointV ptItem, Matrix rotateMat)
{
#if DEBUG
if (rotateMat.Rows != rotateMat.Cols || rotateMat.Cols != 4)
throw new ArgumentNullException("WarpRotate矩阵大小不对");
#endif
return SetRotateMat(ptItem, rotateMat);
}
static PointV SetRotateMat(PointV ptItem, Matrix rotateMat)
{
var ptRo = rotateMat * new Matrix(ptItem.ToArray());//左乘
return new PointV(ptRo.ToArray());
}
}
/////////////////////////////调用例子//////////////////////////////
/// <summary>
/// 旋转
/// </summary>
/// <param name="angle">角度</param>
/// <param name="vector">任意转轴</param>
/// <param name="centerPoint">绕点</param>
/// <returns></returns>
public PointV RotateBy(double angle, PointV vector, PointV centerPoint)
{
var roMat = Transform.GetRotateTransform(angle, vector);
var pt = this - centerPoint;//绕点旁边平移到原点旁边
pt = Transform.WarpRotate(pt, roMat);
return pt + centerPoint;//原点旁边平移到绕点旁边
}
二维旋转
如果不写成矩阵形式,写成函数形式呢？貌似更方便入门和理解.
我发现人家的图不是很好,自己做了一个.
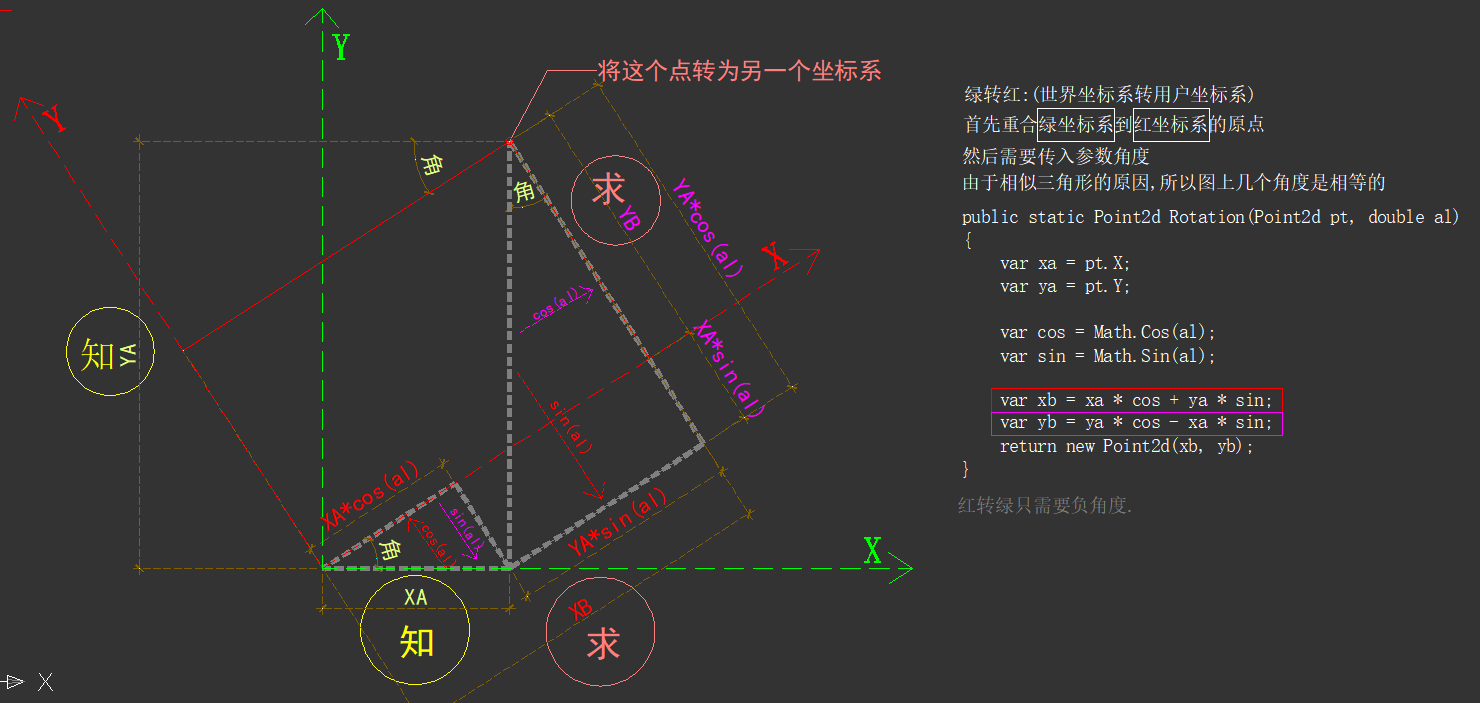
public static Point2d Rotation(Point2d pt, double al)
{
var xa = pt.X;
var ya = pt.Y;
var cos = Math.Cos(al);
var sin = Math.Sin(al);
var xb = xa * cos + ya * sin;
var yb = ya * cos - xa * sin;
return new Point2d(xb, yb);
}
有了二维旋转之后,你就能知道点是如何在原点上围绕Z轴旋转了.
因为Z轴在XOY面上有无数个,所以必须绕原点,否则平移到原点再绕,最后再平移回去.
而二维扩展到三维,无非就是点Z的位置是0,其他轴旋转就是其他轴的点是0,
这样就可以明白了XYZ轴的旋转了,而任意轴旋转看下面的三维旋转.
三维旋转
那么三维的点怎么从用户坐标系到世界坐标系？或者世界转用户？
首先我们要知道这个点所在的坐标系(用户坐标系,物体坐标系,相对坐标系),
拿到这个坐标系的Z轴(提及过的任意轴)
- 重合用户原点到世界原点(就是求向量,向量就是原点开始)
- 重合用户Z轴到世界Z轴,使得剩下世界Z轴可以旋转(不就可以套用了二维旋转了吗).
- 记录下XYZ三个轴的转动角度.
变换必然会依照顺序,出现XYZ按照夹角alx,aly,alz转动,
逆向则为ZYX按照夹角-alz,-aly,-alx转动.
这样即可变换两个坐标系. - 平移回去用户原点.
步骤2就是核心:
重合Z轴只需要旋转XY两个轴即可,如图所示: 原点和P点形成了一个向量(我习惯称作用户z轴)
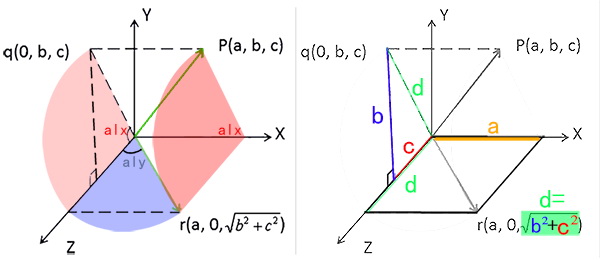
2.1. 把P点投影到YOZ面.获取oq与世界Z轴的夹角alx.
2.2. 通过alx旋转世界X轴后,P点将会变换为r点,r点在XOZ平面上.获取or与世界Z轴角度aly.
2.3. 接着获取alz,看代码就晓得了.
public static partial class MathHelper
{
/// 原理见:http://www.cnblogs.com/graphics/archive/2012/08/10/2627458.html
/// 以及:http://www.doc88.com/p-786491590188.html
/// <summary>
/// 输入一个法向量(用户Z轴),获取它与世界坐标X轴和Y轴的夹角,
/// 旋转这两个夹角可以重合世界坐标的Z轴
/// </summary>
/// <param name="userZxis">用户坐标系的Z轴</param>
/// <param name="alx">输出X轴夹角</param>
/// <param name="aly">输出Y轴夹角</param>
public static void ToWcsAngles(this Vector3d userZxis, out double alx, out double aly)
{
//处理精度
double X = Math.Abs(userZxis.X) < 1e-10 ? 0 : userZxis.X;
double Y = Math.Abs(userZxis.Y) < 1e-10 ? 0 : userZxis.Y;
double Z = Math.Abs(userZxis.Z) < 1e-10 ? 0 : userZxis.Z;
//YOZ面==旋转X轴..投影的
var oq = Point3d.Origin.GetVectorTo(new Point3d(0, Y, Z));
alx = Vector3d.ZAxis.GetAngleTo(oq);
alx = oq.Y > 0 ? alx : Pi2 - alx;
alx = Math.Abs(Pi2 - alx) < 1e-10 ? 0 : alx;
//XOZ面==旋转Y轴..旋转的
var userZ = Math.Pow(Y * Y + Z * Z, 0.5);
var or = Point3d.Origin.GetVectorTo(new Point3d(X, 0, userZ));
aly = Vector3d.ZAxis.GetAngleTo(or);
aly = or.X < 0 ? aly : Pi2 - aly;
aly = Math.Abs(Pi2 - aly) < 1e-10 ? 0 : aly;
}
/// <summary>
/// X轴到向量的弧度,cad的获取的弧度是1PI,所以转换为2PI(上小,下大)
/// </summary>
/// <param name="ve">向量</param>
/// <returns>弧度</returns>
public static double GetAngle2XAxis(this Vector2d ve)
{
double alz = Vector2d.XAxis.GetAngleTo(ve);//观察方向不要设置
alz = ve.Y > 0 ? alz : Pi2 - alz; //逆时针为正,如果-负值控制正反
alz = Math.Abs(Pi2 - alz) < 1e-10 ? 0 : alz;
return alz;
}
/// <summary>
/// X轴到向量的弧度,cad的获取的弧度是1PI,所以转换为2PI(上小,下大)
/// </summary>
public static double GetAngle2XAxis(this Point2d startPoint, Point2d endtPoint)
{
return startPoint.GetVectorTo(endtPoint).GetAngle2XAxis();
}
/// <summary>
/// 三个轴角度
/// 重合两个坐标系的Z轴,求出三个轴旋转角度,后续利用旋转角度正负和次序来变换用户和世界坐标系
/// </summary>
/// <param name="ucs">用户坐标系</param>
/// <param name="alx">坐标系间的X轴旋转角度</param>
/// <param name="aly">坐标系间的Y轴旋转角度</param>
/// <param name="alz">坐标系间的Z轴旋转角度</param>
public static void ToWcsAngles(this CoordinateSystem3d ucs, out double alx, out double aly, out double alz)
{
//ucs可能带有新原点,设置到0,世界坐标系原点重合
var ucs2o = new CoordinateSystem3d(Point3d.Origin, ucs.Xaxis, ucs.Yaxis);
//XY轴通过叉乘求得Z轴,但是这个类帮我求了
ucs2o.Zaxis.ToWcsAngles(out alx, out aly);
//使用户X轴与世界XOY面共面,求出Z轴旋转角
var newXa = ucs2o.Xaxis.RotateBy(alx, Vector3d.XAxis)
.RotateBy(aly, Vector3d.YAxis);
alz = -newXa.GetAngle2XAxis();
}
private static Point3d Wcs2Ucs(this Point3d pt, CoordinateSystem3d ucs)
{
ucs.ToWcsAngles(out double alx, out double aly, out double alz);
pt = new Point3d(pt.X - ucs.Origin.X,
pt.Y - ucs.Origin.Y,
pt.Z - ucs.Origin.Z);
pt = pt.RotateBy(alx, Vector3d.XAxis, Point3d.Origin)
.RotateBy(aly, Vector3d.YAxis, Point3d.Origin)
.RotateBy(alz, Vector3d.ZAxis, Point3d.Origin);
return pt;
}
private static Point3d Ucs2Wcs(this Point3d pt, CoordinateSystem3d ucs)
{
ucs.ToWcsAngles(out double alx, out double aly, out double alz);
//把pt直接放在世界坐标系上,此时无任何重合.
//进行逆旋转,此时向量之间重合.
pt = pt.RotateBy(-alz, Vector3d.ZAxis, Point3d.Origin)
.RotateBy(-aly, Vector3d.YAxis, Point3d.Origin)
.RotateBy(-alx, Vector3d.XAxis, Point3d.Origin);
//平移之后就是点和点重合,此点为世界坐标系.
pt = new Point3d(pt.X + ucs.Origin.X,
pt.Y + ucs.Origin.Y,
pt.Z + ucs.Origin.Z);
return pt;
}
/// <summary>
/// 把一个点从一个坐标系统变换到另外一个坐标系统
/// </summary>
/// <param name="userPt">来源点</param>
/// <param name="source">来源坐标系</param>
/// <param name="target">目标坐标系</param>
/// <returns>目标坐标系的点</returns>
public static Point3d Transform(this Point3d userPt, CoordinateSystem3d source, CoordinateSystem3d target)
{
//世界坐标是独特的
var wcs = Matrix3d.Identity.CoordinateSystem3d;
Point3d pt = Point3d.Origin;
if (Equals(source, target))
pt = userPt;
//al的角度是一样的,旋转方式取决于正负号
else if (!Equals(source, wcs) && !Equals(target, wcs))//用户转用户
pt = userPt.Ucs2Wcs(source).Wcs2Ucs(target);
if (Equals(target, wcs))
pt = userPt.Ucs2Wcs(source);
else if (!Equals(target, wcs))
pt = userPt.Wcs2Ucs(target);
return pt;
}
/// <summary>
/// 获取坐标系统三维
/// </summary>
/// <param name="ed"></param>
/// <param name="wcs"></param>
/// <param name="ucs"></param>
public static void GetWcsUcs(this Editor ed, out CoordinateSystem3d wcs, out CoordinateSystem3d ucs)
{
Matrix3d Ide_wcs = Matrix3d.Identity;//获取世界坐标系
wcs = Ide_wcs.CoordinateSystem3d;
Matrix3d used_ucs = ed.CurrentUserCoordinateSystem;//当前用户坐标系
ucs = used_ucs.CoordinateSystem3d;
}
}
凸度
参考
mac-lee,它已经说得很好了
bulgeconversion-参考链接1
bulgeconversion-参考链接2
已知圆弧的起点端点和凸度计算圆心 防丢链接
说明
A: 此函数将把用于定义Acad圆弧转多边形弧段(顶点,凸度).
B: 还可以从 凸度==0 判断点是否在直线上.
返回:凸度可能是正的,也可能是负的,这取决于通过这三个点的弧线是顺时针路径还是逆时针.
为了尽量避免歧义,在交流的时候不要使用中点和终点,改为腰点和尾点.
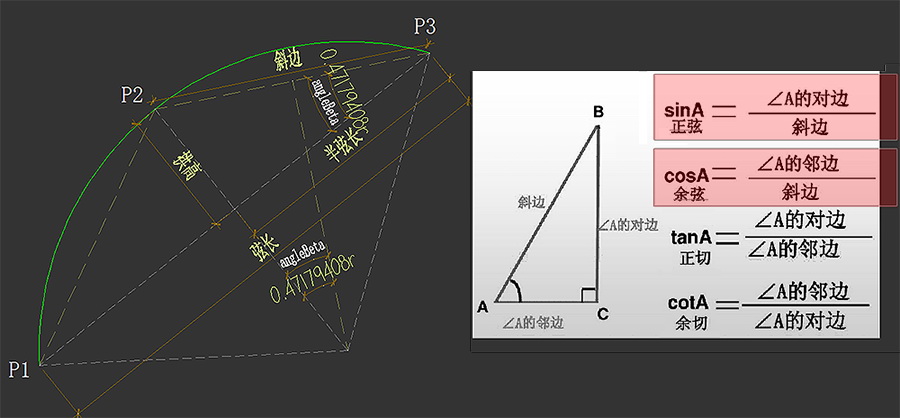
在cad的Polyline属性有pl.GetBulgeAt(i)自带的.
lisp的处理方式:
3-Points to Bulge缩写是 3P to B..感觉怪怪吼!
;; 3-Points to Bulge - Lee Mac
(defun LM:3p->bulge ( pt1 pt2 pt3 )
((lambda ( a ) (/ (sin a) (cos a))) (/ (+ (- pi (angle pt2 pt1)) (angle pt2 pt3)) 2))
)
c#的处理方式:
/// <summary>
/// 凸度的测试命令,点1=圆弧头点,点2=圆弧腰点,点3=圆弧尾点
/// </summary>
[CommandMethod("test_BulgeCenter")]
public void test_BulgeCenter()
{
var dm = Acap.DocumentManager;
Editor ed = dm.MdiActiveDocument.Editor;
var ppo = new PromptPointOptions("");
var pts = new List<Point3d>();
for (int i = 0; i < 3; i++)
{
ppo.Message = $"{Environment.NewLine}点位置{i}:";
var pot = ed.GetPoint(ppo);
if (pot.Status != PromptStatus.OK)
return;
pts.Add(pot.Value);
}
var getBulge = MathHelper.GetArcBulge(pts[0], pts[1], pts[2]);
var center = MathHelper.GetArcBulgeCenter(pts[0].ToPoint2d(), pts[2].ToPoint2d(), getBulge);
ed.WriteMessage($"{Environment.NewLine}凸度是:{getBulge}");
ed.WriteMessage($"{Environment.NewLine}圆心点是:" + center.DebugString());
var arcLength = MathHelper.GetArcLength(pts[0].ToPoint2d(), pts[2].ToPoint2d(), getBulge);
ed.WriteMessage($"{Environment.NewLine}弧长是:{arcLength}");
}
计算凸度
/// http://www.lee-mac.com/bulgeconversion.html
/// <summary>
/// 求凸度,判断三点是否一条直线上
/// </summary>
/// <param name="arc1">圆弧起点</param>
/// <param name="arc2">圆弧腰点</param>
/// <param name="arc3">圆弧尾点</param>
/// <returns>逆时针为正,顺时针为负</returns>
public static double GetArcBulge(Point2d arc1, Point2d arc2, Point2d arc3)
{
double dStartAngle = GetAngle2XAxis(arc2, arc1);
double dEndAngle = GetAngle2XAxis(arc2, arc3);
//求的P1P2与P1P3夹角
var talAngle = (Math.PI - dStartAngle + dEndAngle) / 2;
//凸度==拱高/半弦长==拱高比值/半弦长比值
//有了比值就不需要拿到拱高值和半弦长值了,因为接下来是相除得凸度
double bulge = Math.Sin(talAngle) / Math.Cos(talAngle);
//处理精度
if (bulge > 0.9999 && bulge < 1.0001)
bulge = 1;
else if (bulge < -0.9999 && bulge > -1.0001)
bulge = -1;
else if (Math.Abs(bulge) < 1e-10)
bulge = 0;
return bulge;
}
/// <summary>
/// 求凸度,判断三点是否一条直线上..慢一点
/// </summary>
/// <param name="arc1">圆弧起点</param>
/// <param name="arc2">圆弧腰点</param>
/// <param name="arc3">圆弧尾点</param>
/// <returns>逆时针为正,顺时针为负</returns>
public static double GetArcBulge(this Arc arc)
{
var arc1 = arc.StartPoint;
var arc2 = arc.GetPointAtDist(arc.GetDistAtPoint(arc.EndPoint) / 2);//圆弧的腰点
var arc3 = arc.EndPoint;
return GetArcBulge(arc1, arc2, arc3);
}
/// <summary>
/// 求凸度,判断三点是否一条直线上
/// </summary>
/// <param name="arc" >圆弧</ param>
/// <returns></returns>
public static double GetArcBulge2(this Arc arc)
{
//还有一种求凸度方法是tan(圆心角 / 4),但是丢失了方向,
//再用叉乘来判断腰点方向,从而凸度是否 * -1
double bulge = Math.Tan(arc.TotalAngle / 4); //凸度是圆心角的四分之一的正切
Point3d midpt = arc.GetPointAtDist(arc.GetDistAtPoint(arc.EndPoint) / 2);//圆弧的腰点
Vector3d vmid = midpt - arc.StartPoint; //起点到腰点的向量
Vector3d vend = arc.EndPoint - arc.StartPoint; //起点到尾点的向量
Vector3d vcross = vmid.CrossProduct(vend); //叉乘求正负
//根据右手定则,腰点向量在尾点向量右侧,则叉乘向量Z值为正,圆弧为逆时针
if (vcross.Z < 0)
bulge *= -1;
//处理精度
if (bulge > 0.9999 && bulge < 1.0001)
bulge = 1;
else if (bulge < -0.9999 && bulge > -1.0001)
bulge = -1;
else if (Math.Abs(bulge) < 1e-10)
bulge = 0;
return bulge;
}
/// <summary>
/// 测试凸度函数哪个快
/// </summary>
[CommandMethod("CmdTest_GetArcBulge")]
public void CmdTest_GetArcBulge()
{
var dm = Acap.DocumentManager;
var doc = dm.MdiActiveDocument;
var db = doc.Database;
var ed = doc.Editor;
var arc = new Arc(Point3d.Origin, 20, 0, Math.PI / 2);
TimeHelper.RunTime(() => {
for (int i = 0; i < 500_0000; i++)
{
MathHelper.GetArcBulge(arc);
}
}, "A测试时间是:");
TimeHelper.RunTime(() => {
for (int i = 0; i < 500_0000; i++)
{
MathHelper.GetArcBulge2(arc);
}
}, "B测试时间是:");
}
/// <summary>
/// 测试运行时间
/// </summary>
/// <param name="action"></param>
public static long RunTime(Action action, string str = null)
{
var stopwatch = new Stopwatch();
stopwatch.Start(); //开始监视
action.Invoke(); //执行委托
stopwatch.Stop(); //停止监视
// stopwatch.Restart();//把前面的时间清空
var timespan = stopwatch.ElapsedMilliseconds; //毫秒数
//TimeSpan timespan = stopwatch.Elapsed; //获取当前实例测量得出的总时间
if (str != null)
Debug.WriteLine(str + timespan.ToString() + "毫秒");
return timespan;
}
凸度求圆心
/// http://bbs.xdcad.net/thread-722387-1-1.html
/// <summary>
/// 凸度求圆心
/// </summary>
/// <param name="arc1">圆弧头点</param>
/// <param name="arc3">圆弧尾点</param>
/// <param name="bulge">凸度</param>
/// <returns>圆心</returns>
public static Point2d GetArcBulgeCenter(Point2d arc1, Point2d arc3, double bulge)
{
if (bulge == 0)
throw new ArgumentNullException("凸度为0,此线是平的");
var x1 = arc1.X;
var y1 = arc1.Y;
var x2 = arc3.X;
var y2 = arc3.Y;
var b = (1 / bulge - bulge) / 2;
var x = (x1 + x2 - b * (y2 - y1)) / 2;
var y = (y1 + y2 + b * (x2 - x1)) / 2;
return new Point2d(x, y);
}
凸度求弧长
/// <summary>
/// 凸度求弧长
/// </summary>
/// <param name="arc1">圆弧头点</param>
/// <param name="arc3">圆弧尾点</param>
/// <param name="bulge">凸度</param>
/// <returns></returns>
public static double GetLength(Point2d arc1, Point2d arc3, double bulge)
{
var bowLength = arc1.DistanceTo(arc3); //弦长
var bowLength2 = bowLength / 2; //半弦
var archHeight = Math.Abs(bulge) * bowLength2; //拱高==凸度*半弦
//根据三角函数: (弦长/2)²+(半径-拱高)²=半径²
//再根据:完全平方公式变形: (a+b)²=a²+2ab+b²、(a-b)²=a²-2ab+b²
var r = (bowLength2 * bowLength2 + archHeight * archHeight) / (2 * archHeight); //半径
//求圆心角:一半圆心角[(对边==半弦长,斜边==半径)]; *2就是完整圆心角
var asin = Math.Asin(bowLength2 / r) * 2; //反正弦
//弧长公式: 弧长=绝对值(圆心弧度)*半径...就是单位*比例..缩放过程
var arcLength = asin * r;
return arcLength;
}
凸度求圆弧腰点
/// <summary>
/// 圆弧的腰点
/// </summary>
/// <param name="arc1">圆弧点1</param>
/// <param name="arc3">圆弧点3</param>
/// <param name="bulge">凸度</param>
/// <returns>返回腰点</returns>
/// <exception cref="ArgumentNullException"></exception>
public static Point2d GetArcMidPoint(Point2d arc1, Point2d arc3, double bulge)
{
if (bulge == 0)
throw new ArgumentException("凸度为0,此线是平的");
var center = GetArcBulgeCenter(arc1, arc3, bulge);
var angle1 = center.GetVectorTo(arc1).GetAngle2XAxis();
var angle3 = center.GetVectorTo(arc3).GetAngle2XAxis();
// 利用边点进行旋转,就得到腰点,旋转角/2
// 需要注意镜像的多段线
double angle = angle3 - angle1;
if (bulge > 0)
{
if (angle < 0)
angle += Math.PI * 2;
}
else
{
if (angle > 0)
angle += Math.PI * 2;
}
return arc1.RotateBy(angle / 2, center);
}
反三角函数
由于我经常忘记三角函数和反三角函数之间的关系...敲了一点cad的测试命令.
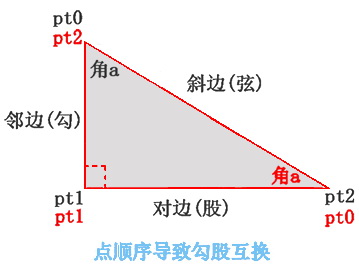
[CommandMethod("test_InverseTrigonometric")]
public void test_InverseTrigonometric()
{
var doc = Acap.DocumentManager.MdiActiveDocument;
var db = doc.Database;
var ed = doc.Editor;
ed.WriteMessage($"{Environment.NewLine}反三角函数");
var ppo = new PromptPointOptions("")
{
AllowNone = false,
};
var pts = new List<Point3d>();
for (int i = 0; i < 3; i++)
{
ppo.Message = $"{Environment.NewLine}选择三角形角点{i}";
var gp = ed.GetPoint(ppo);
if (gp.Status != PromptStatus.OK)
return;
pts.Add(gp.Value);
}
//由于某些实际情况缺少一条边,此时需要求夹角,则使用反三角函数
var 邻边 = pts[0].DistanceTo(pts[1]);
var 对边 = pts[1].DistanceTo(pts[2]);
var 斜边 = pts[2].DistanceTo(pts[0]);
//Math.Cos(angle) == 邻边 / 斜边;
//Math.Sin(angle) == 对边 / 斜边;
//Math.Tan(angle) == 对边 / 邻边;
var acos = Math.Acos(邻边 / 斜边); //反余弦
var asin = Math.Asin(对边 / 斜边); //反正弦
var atan = Math.Atan(对边 / 邻边); //反正切
var atan2 = Math.Atan2(56, 30) * 180 / Math.PI;//(Y,X)与(0,0 X轴)的夹角
ed.WriteMessage($"{Environment.NewLine}角度a是:{asin},{atan},{acos}");
}
它们的实现方式是泰勒展开
高精度反三角函数的实现
导数应用(光线反射)
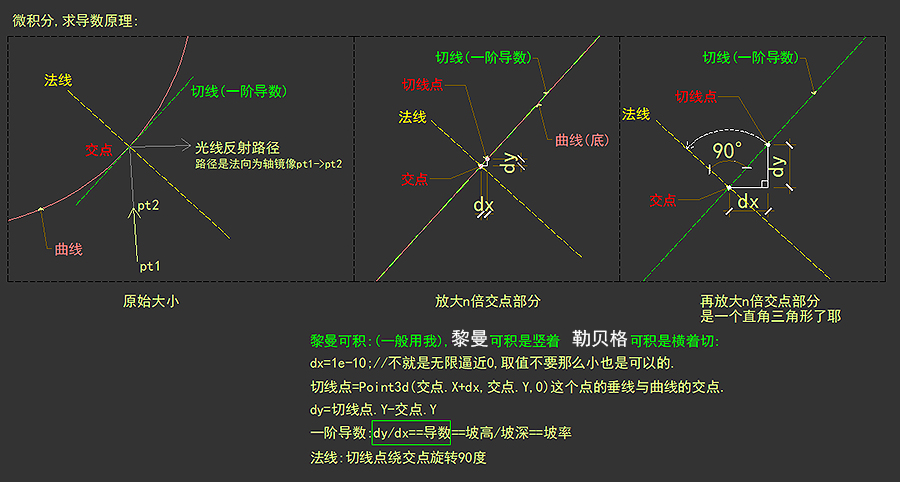
计算方式是:
一阶导数y'=dy/dx=df(x)/dx
二阶导数y''=dy'/dx=[d(dy/dx)]/dx=d²y/dx²=d²f(x)/dx²
...
看一点伪代码,形象的理解一下:
//一阶导数
double GetFirstDerivative(double dy)
{
double dx = 1e-10;//趋近于0
return dy / dx;
}
double 二阶导数(double dy)
{
return GetFirstDerivative(GetFirstDerivative(dy));
}
double 三阶导数(double dy)
{
return GetFirstDerivative(GetFirstDerivative(GetFirstDerivative(dy)));
}
//四阶五阶六阶...无限嵌套就是无限阶...
cad实现
起初我根据群友认为的二阶导数就是法线,实际上求了一个特殊解:只有圆弧的二阶导数等于法线.
而要扩展到曲线的法线,则通用解是切线旋转90度.
using Autodesk.AutoCAD.EditorInput;
using Autodesk.AutoCAD.Geometry;
using Autodesk.AutoCAD.Runtime;
using Autodesk.AutoCAD.DatabaseServices;
using Acap = Autodesk.AutoCAD.ApplicationServices.Application;
using System.Collections.Generic;
using System;
namespace JoinBox
{
public partial class CmdTest
{
[CommandMethod("test_Derivative")]
public void test_Derivative()
{
var dm = Acap.DocumentManager;
var doc = dm.MdiActiveDocument;
var db = doc.Database;
var ed = doc.Editor;
//两点确定射线入射角
var pts = new List<Point3d>();
var ppo = new PromptPointOptions("");
for (int i = 0; i < 2; i++)
{
ppo.Message = $"{Environment.NewLine}测试导数,点位置{i + 1}:";
var pot = ed.GetPoint(ppo);
if (pot.Status != PromptStatus.OK)
return;
pts.Add(pot.Value);
}
var ray0 = new Ray
{
BasePoint = pts[0],
SecondPoint = pts[1],
};
db.Action(tr => {
//获取屏幕内的图元,再获取射中的
var ids = SelectViewportObjectId(ed, tr);
if (ids == null)
return;
foreach (var id in ids)
{
var ent = id.ToEntity(tr);
if (ent is Curve cur)
{
if (ent is not Arc)//测试时候过滤掉无用注释用
continue;
var ptc = new Point3dCollection();
ray0.IntersectWith(cur, Intersect.OnBothOperands, ptc.Collection, (int)IntPtr.Zero, (int)IntPtr.Zero); //得出的所有交点
if (ptc.Count == 0)
continue;
var intPt = ptc[0]; //交点可能是3d点
// 一阶导数是切线
Vector3d yt1 = cur.GetFirstDerivative(intPt);
var ray1 = new Ray
{
BasePoint = intPt,
SecondPoint = new Point3d(yt1.X + intPt.X, yt1.Y + intPt.Y, 0),
};
ray1.ColorIndex = 1;
tr.AddEntityToMsPs(db, ray1);
#if true3
// 只有圆弧的二阶导数是法线
Vector3d yt2 = cur.GetSecondDerivative(intPt);
var ray2 = new Ray
{
BasePoint = intPt,
SecondPoint = new Point3d(yt2.X + intPt.X, yt2.Y + intPt.Y, 0),
};
#else
// 曲线的法线通用解是:切线是旋转90度
var ray2 = ray1.Clone() as Ray;
ray2.EntityRotate(Math.PI / 2, Vector3d.ZAxis, intPt);
#endif
ray2.ColorIndex = 2;
tr.AddEntityToMsPs(db, ray2);
// 射出光线
var ray3 = new Ray
{
BasePoint = intPt,
SecondPoint = pts[0],
};
ray3.EntityMirror(ray2.BasePoint, ray2.SecondPoint, out Entity ray3mr);
ray3mr.ColorIndex = 3;
tr.AddEntityToMsPs(db, ray3mr);
}
}
});
}
/// <summary>
/// 获取当前屏幕的所有图元
/// </summary>
/// <param name="ed"></param>
/// <param name="tr"></param>
/// <returns></returns>
ObjectId[] SelectViewportObjectId(Editor ed, Transaction tr)
{
var view = ed.GetCurrentView();
var cpt = view.CenterPoint;
var w = view.Width / 2;
var h = view.Height / 2;
//先忽略视口原点角度等信息
var min = new Point3d(cpt.X - w, cpt.Y - h, 0);
var max = new Point3d(cpt.X + w, cpt.Y + h, 0);
var ssget = ed.SelectCrossingWindow(min, max);
if (ssget.Status != PromptStatus.OK)
return null;
return ssget.Value.GetObjectIds();
}
}
}
public static partial class EntityEdit
{
// 镜像
public static Matrix3d EntityMirror(this Entity ent,
Point3d point1, Point3d point2, out Entity entity)
{
//计算变换矩阵
Matrix3d mt = Matrix3d.Mirroring(new Line3d(point1, point2));//镜像矩阵
entity = ent.GetTransformedCopy(mt); //这里可能要替换成克隆
return mt;
}
}
public static partial class EntityAdd
{
/// <summary>
/// 将图形添加到数据库的当前空间中
/// </summary>
/// <param name="db">图形数据库</param>
/// <param name="ent">图形对象</param>
/// <returns>图形的ObjectId</returns>
public static ObjectId AddEntityToMsPs(this Transaction tr, Database db, Entity ent)
{
ObjectId entId;
//在位编辑的时候自动加到块内了,而不是模型空间,因为会把临时的数据拷贝回去块表记录上面
//出现eLockViolation 是因 CommandFlags.Session | CommandFlags.Redraw 又没有锁文档
var btRec = tr.GetObject(db.CurrentSpaceId, OpenMode.ForWrite) as BlockTableRecord;
//加图元到块表记录,设定返回值
entId = btRec.AppendEntity(ent);
//更新数据
tr.AddNewlyCreatedDBObject(ent, true);
btRec.DowngradeOpen();
btRec.Dispose();
return entId;
}
}
子函数:
本博客引用: 委托db.Action cad.net 委托无返回值写法
本博客引用: ptc.Collection 二度封装Point3dCollection
二阶导数
那曲线的二阶导数有什么用呢？
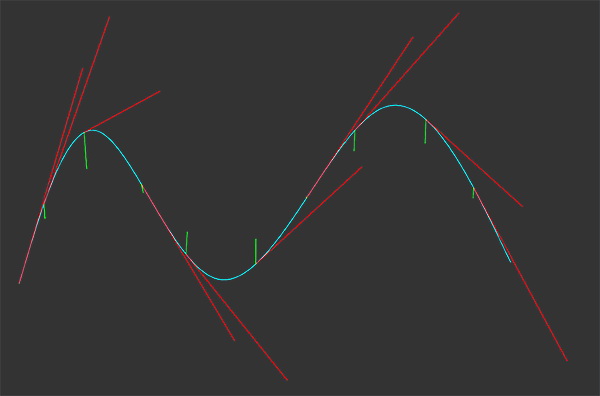
它表达斜率的变化率,所以越凸的地方值越大.
看图上绿色的部分,长度越长表示值越大,表示你油门踩得越深,然后也表达加速度了.
所以运动控制上面有用.
而对椭圆用二阶导数,会得到椭圆中心点,而不是两个焦点.
椭圆实际上是任意轴观察的圆形,这样就求出圆心了.
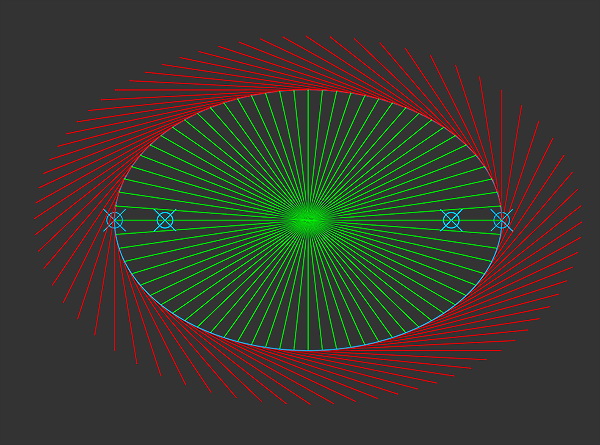
三阶导数
它是变化率的变化率,它有什么用呢？
找拐点
相关阅读
取余(取模)
9%2=>1
9/2=4.5
则用4*2=8;商整数部分*除数
再用9-8=1;结果就是余数
2%40=>2
2/40=0.05
则用0*40=0;商整数部分*除数
再用2-0=2;结果就是余数
但是除数为2的幂次方,减少使用除法器(就是减少牛顿迭代),实现加速
即：
a & (2^n - 1)
它可以做什么?
A: 如果有一个一维数组,你需要按照每4个分一份,
那么就可以循环的时候 i%4==0 每次new List Add(i1,i2,i3,i4)从而实现切割.
B: 哈希值%3就是将数据大致均匀的分到三分之一,看得出%3就是在[0,2]闭区间:
0%3==0
1%3==1
2%3==2
3%3==0
100%3==1
C: 分库分表
一致性哈希算法
快速模运算
public static ulong ModPow(ulong baseValue, ulong exponent, ulong modulus)
{
// 初始化结果为1,因为任何数的0次方都是1
ulong result = 1;
// 底数对模数取模,以防底数过大
baseValue %= modulus;
// 当指数不为0时,继续循环
while (exponent > 0)
{
// 如果当前指数是奇数,将底数乘到结果上,并取模
if ((exponent & 1) == 1)
result = (result * baseValue) % modulus;
// 底数平方并取模
baseValue = (baseValue * baseValue) % modulus;
// 指数右移一位（等同于除以2）
exponent >>= 1;
}
// 返回结果
return result;
}
(完)
