矩阵乘法

---

矩阵

矩阵 (matrix) 是一个由数排列形成的矩形，例如

\[A=\left[ \begin{matrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \end{matrix} \right] \]

这是一个 \(2 \times 3\) 的矩阵。翻转行列得到转置矩阵 \(A^T\)

矩阵加法

矩阵行、列数都相等时才有矩阵加减法。为对应位置的元素相加减。

\[\left[\begin{matrix}1&1&1\\1&1&1\end{matrix}\right] + \left[\begin{matrix}1&2&3\\4&5&6\end{matrix}\right] = \left[\begin{matrix}2&3&4\\5&6&7\end{matrix}\right] \]

矩阵乘法

\(C=A\times B\) ，仅当 \(A\) 的列数等于 \(B\) 的行数。

若 \(A\) 是 \(m\times n\) 的矩阵，\(B\) 是 \(n \times p\) 的矩阵，\(C\) 是 \(m\times p\) 的矩阵。

\[c_{ij} = \sum_{k=1}^{n}a_{ik} \cdot b_{kj} \\ i\in\left[1,m\right]\;,\;j\in[1,p] \]

即“一行乘一列得一数”：

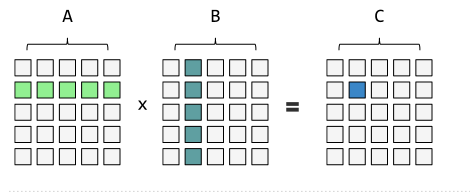
很容易发现矩乘不满足交换律，但满足结合律。于是矩阵求幂可以倍增加速。

看这样的一题：

求斐波那契数列的第 n 项对 1e9+7 取模。n 在 long long 范围内。

\[f_n=f_{n-1}+f_{n-2} \]

O(n) 递推很显然做不了，但是矩阵乘法很大一个用处就是加速递推。

\[\left[\begin{matrix}f_{i}&f_{i-1}\end{matrix}\right]= \left[\begin{matrix}f_{i-1}&f_{i-2}\end{matrix}\right] \times \left[\begin{matrix}1&1\\1&0\end{matrix}\right]= \left[\begin{matrix}f_2&f_1\end{matrix}\right]\times \left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{i-2} \]

矩阵快速幂

单位矩阵 \(I_n = \left[\begin{matrix}1&0&\cdots&0\\0&1&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&1\end{matrix}\right]\) 即左上到右下为1的正方形矩阵， \(I^n=I\)

struct Mrx { long long G[N][N]; } I, emp;

inline void Mrxmul(Mrx A, Mrx B, Mrx &Z) {
	memset(Z.G, 0, sizeof(Z.G));
	for(int i = 1; i <= n; ++i) 
	for(int j = 1; j <= n; ++j) 
	for(int k = 1; k <= n; ++k) 
		Z.G[i][j] = (Z.G[i][j] + A.G[i][k] * B.G[k][j]) % mod;
}
inline Mrx Pow(Mrx A, ll b) {
	Mrx res = I;
	while(b) {
		if(b & 1) Mrxmul(res, A, res);
		Mrxmul(A, A, A);
		b >>= 1;
	}
	return res;
}