树链剖分 「笔记」
考虑这个问题:
要求在树上进行两种操作
1.把 \(x\) 到 \(y\) 的简单路径上所有点的权值加 \(k\)
2.询问 \(x\) 到 \(y\) 的简单路径上的点权和
(任意单个问题都可以通过树上差分或树上前缀和维护,合起来不就是树上线段树?)
1.轻重链剖分
类似在数列中维护区间和,树链剖分把树剖分成多条链,可以用各种数据结构维护链。
模板题:轻重链剖分
做以下定义:
重儿子:子树大小最大的儿子
重边:连重儿子的边
重链:重边连起来的链
轻儿子、边、链:其它的儿子、边、链
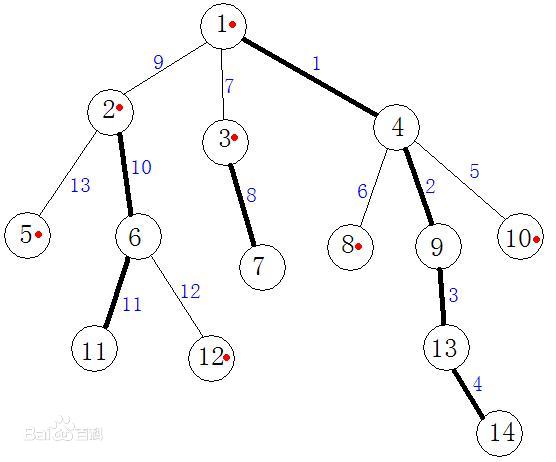
用两个DFS预处理
DFS序标号节点,DFS时先走重儿子,保证每条重链的 \(dfn\) 连续。
然后用DFS序建立线段树。
\(tim\) 时间戳,\(fa\) 父亲节点编号,\(dep\) 深度,\(siz\) 子树大小,\(son\) 重儿子编号,
\(dfn\) DFS序,\(x\_u\) DFS序向节点编号的映射,\(top\) 链顶节点,轻儿子的链顶是它自己
int tim;
int fa[N], dep[N], siz[N], son[N], dfn[N], x_u[N], top[N];
void Dfs1(int x, int ff) { // 处理fa, dep, siz, son
fa[x] = ff; dep[x] = dep[ff] + 1; siz[x]++;
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(to != ff) {
Dfs1(to, x);
siz[x] += siz[to];
if(siz[to] > siz[son[x]]) son[x] = to;
}
}
}
void Dfs2(int x, int ff) { // 处理dfn, x_u, top. ff为链顶节点
dfn[x] = ++tim, x_u[dfn[x]] = x;
top[x] = ff;
if(!son[x]) return ;
Dfs2(son[x], ff); // 先走重儿子
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(!dfn[to]) Dfs2(to, to);
}
}
线段树部分
显然子树内DFS序是个连续的区间,3、4操作可以简单做。
// 最普通的线段树
struct Tree {
int l, r;
long long sum, lazy;
} tree[N << 2];
void Update(int x) {
tree[x].sum = (tree[x << 1].sum + tree[x << 1 | 1].sum) % mod;
}
void Pushdown(int x) {
long long k = tree[x].lazy;
k %= mod;
tree[x].lazy = 0;
tree[x << 1].lazy += k, tree[x << 1 | 1].lazy += k;
tree[x << 1].lazy %= mod, tree[x << 1 | 1].lazy %= mod;
tree[x << 1].sum += k * (tree[x << 1].r - tree[x << 1].l + 1);
tree[x << 1].sum %= mod;
tree[x << 1 | 1].sum += k * (tree[x << 1 | 1].r - tree[x << 1 | 1].l + 1);
tree[x << 1 | 1].sum %= mod;
}
void Build(int x, int l, int r) {
tree[x].l = l, tree[x].r = r;
if(l == r) {
tree[x].sum = a[x_u[l]] % mod; // 用dfn建树
return ;
}
int mid = (l + r) >> 1;
Build(x << 1, l, mid), Build(x << 1 | 1, mid + 1, r);
Update(x);
}
void Addsum(int x, int l, int r, long long k) {
if(tree[x].l >= l && tree[x].r <= r) {
tree[x].sum += k * (tree[x].r - tree[x].l + 1) % mod;
tree[x].sum %= mod;
tree[x].lazy = (tree[x].lazy + k) % mod;
return ;
}
if(tree[x].lazy) Pushdown(x);
int mid = (tree[x].l + tree[x].r) >> 1;
if(l <= mid) Addsum(x << 1, l, r, k);
if(r > mid) Addsum(x << 1 | 1, l, r, k);
Update(x);
}
long long Reqsum(int x, int l, int r) {
if(tree[x].l >= l && tree[x].r <= r) return tree[x].sum % mod;
long long res = 0;
if(tree[x].lazy) Pushdown(x);
int mid = (tree[x].l + tree[x].r) >> 1;
if(l <= mid) res += Reqsum(x << 1, l, r);
if(r > mid) res += Reqsum(x << 1 | 1, l, r);
return res % mod;
}
考虑1、2操作怎么做
把 \(x,y\) 沿着重链往上跳,直到它们跳到同一条重链上,最后考虑 \(x, y\) 之间的这一段。
具体就是当 \(top_x \neq top_y\) 时,将 \(dep_{top}\) 较大的跳到 \(fa_{top}\) 并处理经过的这条重链,因为每条重链的DFS序是连续的,所以可以在线段树上区间操作。
void Pathadd(int x, int y, long long k) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 跳top深度大的
Addsum(1, dfn[top[x]], dfn[x], k); // 将这条重链加上k
x = fa[top[x]];
}
if(dfn[x] > dfn[y]) swap(x, y);
Addsum(1, dfn[x], dfn[y], k);
}
long long Pathsum(int x, int y) {
long long res = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
res += Reqsum(1, dfn[top[x]], dfn[x]);
res %= mod;
x = fa[top[x]];
}
if(dfn[x] > dfn[y]) swap(x, y);
res += Reqsum(1, dfn[x], dfn[y]);
return res % mod;
}
那么这题就可以做了……
点击展开代码
#include "iostream"
#include "cstdio"
#include "algorithm"
using namespace std;
const int N = 1e5 + 5, M = 1e5 + 5;
int n, m, root, mod;
long long a[N];
int head[N], cnt;
struct Edge{
int to, nxt;
} edge[M << 1];
void Add(int from, int to) {
edge[++cnt].to = to; edge[cnt].nxt = head[from];
head[from] = cnt;
}
int tim;
int fa[N], dep[N], siz[N], son[N], dfn[N], x_u[N], top[N];
void Dfs1(int x, int ff) {
fa[x] = ff; dep[x] = dep[ff] + 1; siz[x]++;
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(to != ff) {
Dfs1(to, x);
siz[x] += siz[to];
if(siz[to] > siz[son[x]]) son[x] = to;
}
}
}
void Dfs2(int x, int ff) {
dfn[x] = ++tim, x_u[dfn[x]] = x;
top[x] = ff;
if(!son[x]) return ;
Dfs2(son[x], ff);
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(!dfn[to]) Dfs2(to, to);
}
}
struct Tree {
int l, r;
long long sum, lazy;
} tree[N << 2];
void Update(int x) {
tree[x].sum = (tree[x << 1].sum + tree[x << 1 | 1].sum) % mod;
}
void Pushdown(int x) {
long long k = tree[x].lazy;
k %= mod;
tree[x].lazy = 0;
tree[x << 1].lazy += k, tree[x << 1 | 1].lazy += k;
tree[x << 1].lazy %= mod, tree[x << 1 | 1].lazy %= mod;
tree[x << 1].sum += k * (tree[x << 1].r - tree[x << 1].l + 1);
tree[x << 1].sum %= mod;
tree[x << 1 | 1].sum += k * (tree[x << 1 | 1].r - tree[x << 1 | 1].l + 1);
tree[x << 1 | 1].sum %= mod;
}
void Build(int x, int l, int r) {
tree[x].l = l, tree[x].r = r;
if(l == r) {
tree[x].sum = a[x_u[l]] % mod;
return ;
}
int mid = (l + r) >> 1;
Build(x << 1, l, mid), Build(x << 1 | 1, mid + 1, r);
Update(x);
}
void Addsum(int x, int l, int r, long long k) {
if(tree[x].l >= l && tree[x].r <= r) {
tree[x].sum += k * (tree[x].r - tree[x].l + 1) % mod;
tree[x].sum %= mod;
tree[x].lazy = (tree[x].lazy + k) % mod;
return ;
}
if(tree[x].lazy) Pushdown(x);
int mid = (tree[x].l + tree[x].r) >> 1;
if(l <= mid) Addsum(x << 1, l, r, k);
if(r > mid) Addsum(x << 1 | 1, l, r, k);
Update(x);
}
long long Reqsum(int x, int l, int r) {
if(tree[x].l >= l && tree[x].r <= r) return tree[x].sum % mod;
long long ans = 0;
if(tree[x].lazy) Pushdown(x);
int mid = (tree[x].l + tree[x].r) >> 1;
if(l <= mid) ans += Reqsum(x << 1, l, r);
if(r > mid) ans += Reqsum(x << 1 | 1, l, r);
return ans % mod;
}
void Pathadd(int x, int y, long long k) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
Addsum(1, dfn[top[x]], dfn[x], k);
x = fa[top[x]];
}
if(dfn[x] > dfn[y]) swap(x, y);
Addsum(1, dfn[x], dfn[y], k);
}
long long Pathsum(int x, int y) {
long long res = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
res += Reqsum(1, dfn[top[x]], dfn[x]);
res %= mod;
x = fa[top[x]];
}
if(dfn[x] > dfn[y]) swap(x, y);
res += Reqsum(1, dfn[x], dfn[y]);
return res % mod;
}
int main() {
scanf("%d%d%d%d", &n, &m, &root, &mod);
for(int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
for(int i = 1; i < n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
Add(x, y), Add(y, x);
}
Dfs1(root, 0); Dfs2(root, root);
Build(1, 1, n);
while(m--) {
int o; scanf("%d", &o) ;
if(o == 1) {
int x, y; long long z;
scanf("%d%d%lld", &x, &y, &z);
Pathadd(x, y, z);
}
if(o == 2) {
int x, y;
scanf("%d%d", &x, &y);
printf("%lld\n", Pathsum(x, y));
}
if(o == 3) {
int x; long long z;
scanf("%d%lld", &x, &z);
Addsum(1, dfn[x], dfn[x] + siz[x] - 1, z);
}
if(o == 4) {
int x;
scanf("%d", &x);
printf("%lld\n", Reqsum(1, dfn[x], dfn[x] + siz[x] - 1));
}
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号