Luogu P1183 多边形的面积 「解题报告」&&「用向量积计算多边形面积」笔记

P1183 多边形的面积

---

Luogu

题意

---

给出一多边形的\(n\)个顶点，求它的面积。多边形的边都是垂直或平行于坐标轴的。

解析

---

向量积

\(\vec{a}\cdot\vec{b}\) 可以解释为以 \(a\) 和 \(b\) 为邻边的平行四边形面积

\[\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\sin\theta \]

因为本题中 \(\theta=90^\circ\) 所以 \(\sin\theta=1\)

求三角形ABC的面积，根据向量积的意义，得到：\(S=|\vec{AB}\times\vec{AC}|/2\)

于是

求多边形面积的方法就是用剖分来做的，把多边形分成若干个三角形，求每个三角形的面积。

以顶点逆时针排列为例剖分：

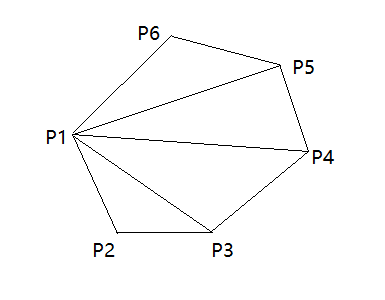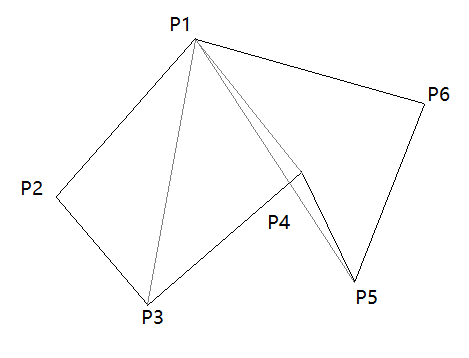对于三角形 \(P_1P_aP_b\) 其面积的正负取决于它是右手系还是左手系（注意是逆时针顶点

左手系，负面积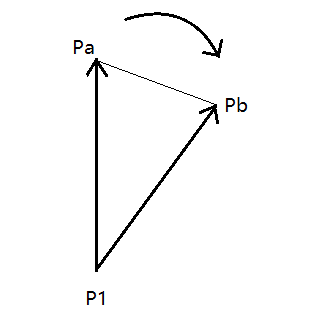	右手系，正面积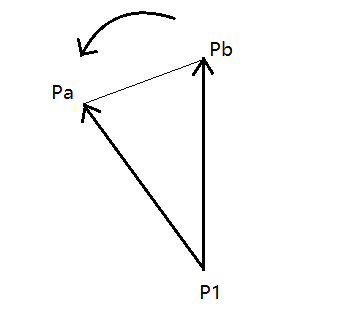

剖分的顶点默认\((0,0)\)，于是可以得出计算多边形面积的公式

\[S=[\sum^{n-1}_1{(\vec{PP_i}\times\vec{PP_{i+1}})+(\vec{PP_n}\times\vec{PP_1})}]\div2 \\\quad\:\:\:\:=[\sum_1^{n-1}{(x_iy_{i+1}-x_{i+1}y_i)+(x_ny_1-x_1y_n)}]\div2 \]

代码

---

#include<iostream>
using namespace std;
int n;
double ans;
struct node
{
	int x;int y;
}dot[101];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>dot[i].x>>dot[i].y;
	for(int i=1;i<=n;i++)
		ans+=(dot[i].x*dot[i+1].y-dot[i+1].x*dot[i].y);
	ans+=(dot[n].x*dot[1].y-dot[1].x*dot[n].y);
	cout<<ans/2<<endl;
	return 0;
}