李超线段树 (Li-Chao Segment Tree)

李超线段树，顾名思义，就是线段树的一个变种。说来惭愧，我在ACM生涯第二年才知道这么个东西的存在，所以赶紧写博客交学费。

李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构。它常被用来处理这样一种形式的问题：给定一个平面直角坐标系，支持动态插入一条线段，询问从某一个位置  向下看能看到的最高的一条线段（也就是给一条竖线，问这条竖线与所有线段的最高的交点。

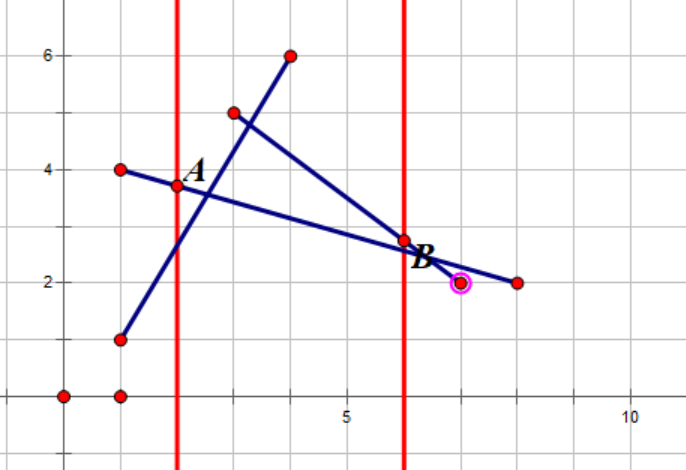
如上图，有三条线段，两条红色竖线代表两个询问，则点  与点  就是询问到的答案。

李超线段树的核心是维护每个区间的“最优势线段”，即在每个区间的中点处最高的线段。询问时我们可以对所有包含横坐标为  的位置的区间上的最优势线段计算答案，最后取个  。

其实这就相当于维护一个记录当前区间最高线段的，不下传标记的线段树。（显然如果我们访问到的区间内只包含询问的横坐标，那么这个区间的最优势线段就是答案线段，所以这样统计包含答案是能保证正确性的）

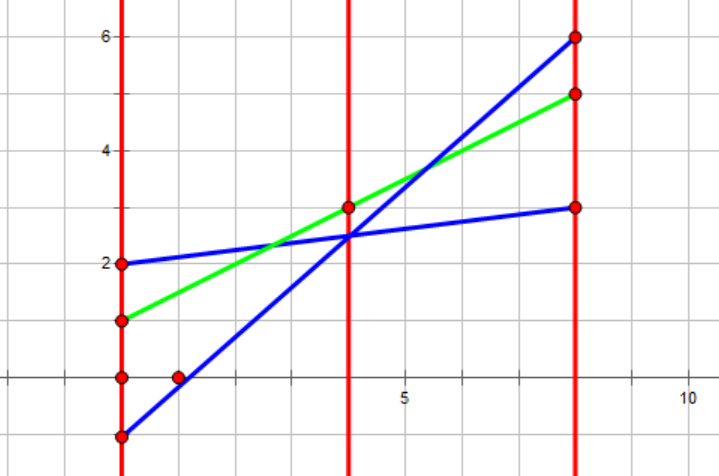
如上图，对于区间$[0,8][0,8]，绿色线段是“最优势线段”$

对于修改，我们先把线段的值域分割到线段树的区间上，每次访问一个完整的包含在线段值域中的区间时：
  1. 若当前区间还没有记录最优势线段，则记录最优势线段并返回。
  2. 若当前区间的最优势线段被插入的线段完全覆盖，则把最优势线段修改为被插入线段并返回。
  3. 若当前区间的最优势线段把被插入线断完全覆盖，则直接返回。
  4. 若当前区间最优势线段与被插入线段有交，则先判断哪条线段在当前区间更优，并把更劣的线段下传到交点所在子区间。（交点两边的部分被这两条线段分别控制，而我们已经让在中点更优的那条线段作为区间最优势线段，因此更劣的那条线段只有可能在交点所在子区间超过当前区间的最优势线段）

下面一起来剖析一下代码。

线段树主体部分：(#define lson curpos<<1    #define rson curpos<<1|1  代码里忘记写了)

const int maxn = 1e5 + 10;
//思来想去，李超线段树的节点名字还是叫Interval而不是Line
//因为这棵线段树以区间为核心，维护的是每一个区间的最优势线段
//写得很长是为了方便初学者理解
struct Interval {
    double k, b; //区间最优势线段的k,b
    int l, r, flag; //l,r为区间。flag为该区间已经记录最优势线段标记。
    Interval() {}
    Interval(int a, int b, double c, double d) {
        this->l = a, this->r = b, this->k = c, this->b = d;
    }
    double calc(const int pos)const { //返回线段在x处的y值
        return k * pos + b;
    }
    int cross(const Interval &rhs)const { //求两线段交点的横坐标
        return floor((b - rhs.b) / (rhs.k - k));
    }
} segt[maxn << 2];

建树：

//因为李超线段树以区间为核心，所以建树时main函数调用build(xOy平面最左端,xOy平面最右端，1);
void build(int curpos, int curl, int curr) {
    segt[curpos].k = segt[curpos].b = 0;
    segt[curpos].l = 1; segt[curpos].r = (int)5e4;
    if (curl == curr) return;
    int mid = curl + curr >> 1;
    build(lson, curl, mid); build(rson, mid + 1, curr);
}

插入线段：

//插入新线段并维护所有区间最优势线段信息
void update(int curpos, int curl, int curr, Interval k) {
    if (k.l <= curl && curr <= k.r) { //被插入线段完全覆盖了当前区间
        //如果当前区间还没有最优势线段，直接标记
        if (!segt[curpos].flag) segt[curpos] = k, segt[curpos].flag = 1;
        //如果被插入线段优于区间最优势线段，更新之
        else if (k.calc(curl) - segt[curpos].calc(curl) > eps && k.calc(curr) - segt[curpos].calc(curr) > eps) segt[curpos] = k;
        //如果被插入线段只有一端优于最优势线段，则检查
        else if (k.calc(curl) - segt[curpos].calc(curl) > eps || k.calc(curr) - segt[curpos].calc(curr) > eps) {
            int mid = curl + curr >> 1;
            if (k.calc(mid) - segt[curpos].calc(mid) > eps) { //这里很关键，要看区间中点哪条线段更优
                Interval tmp = k; k = segt[curpos]; segt[curpos] = tmp;
            }
            if (k.cross(segt[curpos]) - mid < -eps) update(lson, curl, mid, k);
            else update(rson, mid + 1, curr, k);
        }
    } else { //若不优于最优势线段，则检查左右区间
        int mid = curl + curr >> 1;
        if (k.l <= mid) update(lson, curl, mid, k);
        if (k.r > mid) update(rson, mid + 1, curr, k);
    }
}

查询：

//查询区间最优势线段在x处取值
double query(int curpos, int curl, int curr, int x) {
    if (curl == curr) return segt[curpos].calc(x);
    int mid = curl + curr >> 1;
    double ans = segt[curpos].calc(x);
    if (x <= mid) return max(ans, query(lson, curl, mid, x));
    else return max(ans, query(rson, mid + 1, curr, x));
}

 

复杂度分析：

  修改部分：我们每次把一条线段的值域分隔到$\mathrm{O(logn)个区间，每个区间最多把标记下传O(logn)层，因此修改的时间复杂度为O(log2n)。（但实测常数很小）}$

  查询部分：每次在线段树上从上到下扫一遍，时间复杂度为$\mathrm{O(logn)。}$

 

给出一道李超线段树裸题，bzoj1568 (https://lydsy.com/JudgeOnline/problem.php?id=1568)

#include <bits/stdc++.h>
#define ll long long
#define pb push_back
#define mp make_pair
#define sot(a,b) sort(a+1,a+1+b)
#define rep1(i,a,b) for (int i=a;i<=b;i++)
#define eps 1e-12
#define int_inf (1<<30)-1
#define ll_inf (1LL<<62)-1
#define lson curpos<<1
#define rson curpos<<1|1

using namespace std;

const int maxn = 1e5 + 10;
struct Line
{
    double k, b;
    int l, r, flag;
    Line() {}
    Line(int a, int b, double c, double d)
    {
        this->l = a, this->r = b, this->k = c, this->b = d;
    }
    double calc(const int pos)const
    {
        return k * pos + b;
    }
    int cross(const Line &rhs)const
    {
        return floor((b - rhs.b) / (rhs.k - k));
    }
} segt[maxn << 2];

int n; char op[10];

void build(int curpos, int curl, int curr)
{
    segt[curpos].k = segt[curpos].b = 0;
    segt[curpos].l = 1; segt[curpos].r = (int)5e4;
    if (curl == curr) return;
    int mid = curl + curr >> 1;
    build(lson, curl, mid); build(rson, mid + 1, curr);
}

void update(int curpos, int curl, int curr, Line k)
{
    if (k.l <= curl && curr <= k.r)
    {
        if (k.calc(curl) - segt[curpos].calc(curl) > eps && k.calc(curr) - segt[curpos].calc(curr) > eps) segt[curpos] = k;
        else if (k.calc(curl) - segt[curpos].calc(curl) > eps || k.calc(curr) - segt[curpos].calc(curr) > eps)
        {
            int mid = curl + curr >> 1;
            if (k.calc(mid) - segt[curpos].calc(mid) > eps)
            {
                Line tmp = k; k = segt[curpos]; segt[curpos] = tmp;
            }
            if (k.cross(segt[curpos]) - mid < -eps) update(lson, curl, mid, k);
            else update(rson, mid + 1, curr, k);
        }
    }
    else
    {
        int mid = curl + curr >> 1;
        if (k.l <= mid) update(lson, curl, mid, k);
        if (k.r > mid) update(rson, mid + 1, curr, k);
    }
}

double query(int curpos, int curl, int curr, int x)
{
    if (curl == curr) return segt[curpos].calc(x);
    int mid = curl + curr >> 1;
    double ans = segt[curpos].calc(x);
    if (x <= mid) return max(ans, query(lson, curl, mid, x));
    else return max(ans, query(rson, mid + 1, curr, x));
}

int main()
{
    scanf("%d", &n);
    build(1, 1, (int)5e4);
    rep1(i, 1, n)
    {
        scanf("%s", op);
        if (op[0] == 'P')
        {
            double s, p;
            scanf("%lf%lf", &s, &p);
            Line now = Line(1, 50000, p, s - p);
            update(1, 1, (int)5e4, now);
        }
        else
        {
            int x; scanf("%d", &x);
            int ans = (int)floor(query(1, 1, (int)5e4, x) / 100);
            printf("%d\n", ans);
        }
    }
    return 0;
}

 其他相关题目：

bzoj 3938 4515

 

---

Reference：

算法｜李超线段树初步（算法讲解+例题）：https://ac.nowcoder.com/discuss/180365