UVA11255 Necklace

Description

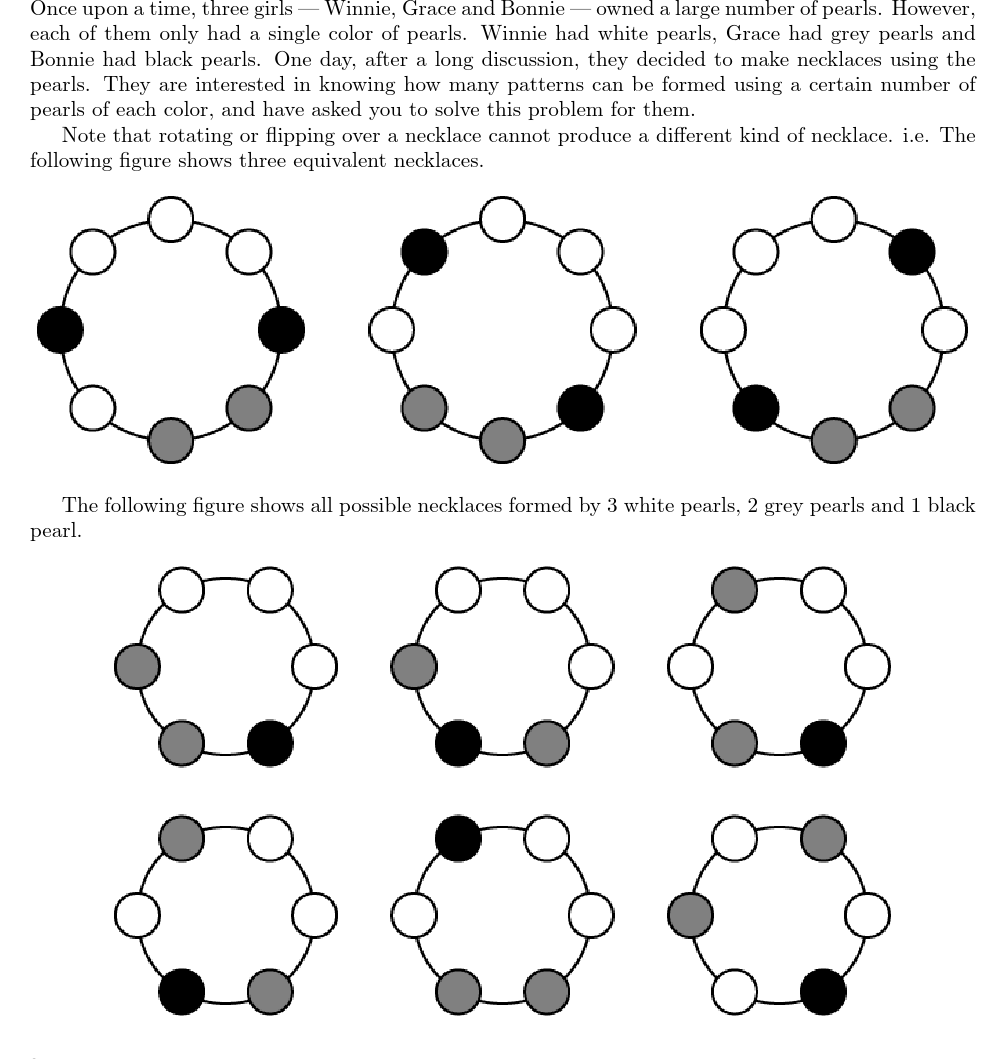
Solution

对于旋转，共有$n$种置换，第$i$种置换的循环节长度为$gcd(i,n)$，那么说明循环节长度为$d$的置换共有$\varphi (\frac nd)$种

当$n$为偶数时，有$\frac n2$种置换不过任何点，另外$\frac n2$种经过两个点，循环节分别为$\frac n2$个和$\frac n2 +1$个

当$n$为奇数时，有$n$种置换只过一个点，循环节有$\frac{n+1}{2}$个

分类讨论，每种变换的不动点个数可以由DP求出

置换群大小为$2n$

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
long long T,n,a,b,c,siz[45],tot,ans,dp[45][45][45];
inline int read()
{
    int f=1,w=0;
    char ch=0;
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') w=(w<<1)+(w<<3)+ch-'0',ch=getchar();
    return f*w;
}
long long phi(int x)
{
    long long ret=x,lim=sqrt(x);
    for(int i=2;i<=lim;i++)
    {
        if(!(x%i))
        {
            ret-=ret/i;
            while(!(x%i)) x/=i;
        }
    }
    if(x!=1) ret-=ret/x;
    return ret;
}
long long DP()
{
    memset(dp,0,sizeof(dp));
    dp[0][0][0]=1;
    for(int i=1;i<=tot;i++) for(int x=a;~x;x--) for(int y=b;~y;y--) for(int z=c;~z;z--)
    {
        if(x>=siz[i]) dp[x][y][z]+=dp[x-siz[i]][y][z];
        if(y>=siz[i]) dp[x][y][z]+=dp[x][y-siz[i]][z];
        if(z>=siz[i]) dp[x][y][z]+=dp[x][y][z-siz[i]];
    }
    return dp[a][b][c];
}
int main()
{
    T=read();
    for(;T;T--)
    {
        a=read(),b=read(),c=read(),n=a+b+c,ans=0;
        for(int i=1;i<=n;i++) if(!(n%i))
        {
            tot=i;
            for(int j=1;j<=tot;j++) siz[j]=n/i;
            ans+=phi(n/i)*DP();
        }
        if(n&1)
        {
            tot=n/2+1,siz[tot]=1;
            for(int i=1;i<tot;i++) siz[i]=2;
            ans+=n*DP();
        }
        else
        {
            tot=n/2;
            for(int i=1;i<=tot;i++) siz[i]=2;
            ans+=n/2*DP();
            siz[tot]=siz[tot+1]=1,++tot;
            ans+=n/2*DP();
        }
        printf("%lld\n",ans/n/2);
    }
    return 0;
}