【笔记】震惊!世上最接地气的字符串浅谈(Trie && AC自动机 && Manacher)
震惊!世上最接地气的字符串浅谈(Trie && AC自动机 && Manacher)
笔者过于垃圾,肯定会有错的地方,欢迎各位巨佬指正,感激不尽!
Luogu id 章鱼那个哥,uid:87075
Trie树
干啥子用的
没什么用,可以 \(O(N)\) 匹配一个串,找字符串前缀,当然还可以做最大 \(Xor\) 和什么的。
怎么写
其实就是每一个节点有字符种数个指针,每次扫描整个字符串,如果没有该子节点,就新建一个,再往下走,举个例子:
插入字符串 car,care,cat。
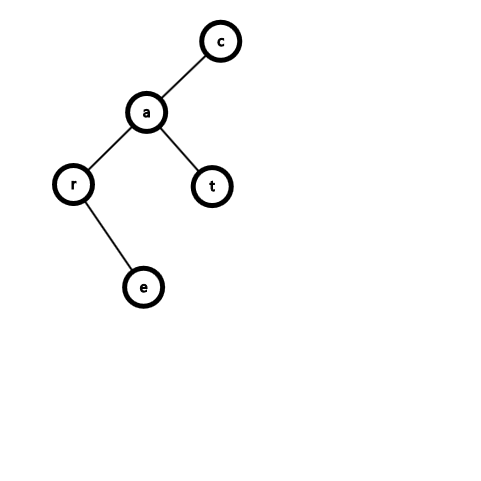
最后到字符串结尾打个标记
代码
int tot;
inline int Insert(const char str[]){
int len=strlen(str),p=0;
for(int i=0;i<len;++i){
int ch=str[i]-'a';
if(!trie[p][ch]) trie[p][ch]=++tot;
p=trie[p][ch];
}
fin[p]=true;
}
inline bool Match(const char str[]){
int len=strlen(str),p=0;
for(int i=0;i<len;++i){
int ch=str[i]-'a';
if(!trie[p][ch]) return false;
p=trie[p][ch];
}
return fin[p];
}
小扩展
-
可以求出包含当前单词的前缀的有几个单词(只要把fin到字符串结尾时加加,Match的时候累加fin)
-
给出一个序列的数字,求最大的Xor对。
二进制分解每个数从高位到低位插入字典树
从大往小走,如果有这个节点,那就往相反的数值走,如果没有只能走相同节点。
对于每个节点做一遍,取最大值。
其他大概还是靠的是直觉把。。。
AC自动机
干啥子用的
可以支持一个文本串,多个模式串
怎么写
考虑对Trie进行改造。引入fail指针。
Trie树的失配指针是指向:沿着其父节点 的 失配指针,一直向上,直到找到拥有当前这个字母的子节点 的节点 的那个子节点
喵的yyb这是什么话啊,给人讲的吗?
举个例子:其实就是如果有文本串hisher和模式串his,her,she
那么当匹配完his我们这个时候跳s的fail跳到了she里的s,再匹配后我们发现his后面没有h,那么就跳到前一个字母的fail指针指向的h也就是she中的h。
其实AC自动机十分适合模拟来理解,最好画画图。
那么怎么求出失配指针呢?
可以bfs,如果有这个儿子,就把这个儿子的失配指针订成当前的这个节点的失配指针的同指针儿子,没有就直接把儿子改成失配指针的同指针儿子。
匹配的时候只要每到一个字符,无脑跳fail
代码
inline void Insert(const char str[],int id){
int len=strlen(str+1),p=0;
for(int i=1;i<=len;++i){
int ch=str[i]-'a';
if(!AC[p].son[ch]) AC[p].son[ch]=++tot;
p=AC[p].son[ch];
}
AC[p].end=id;
}
inline void MakeFail(){
queue <int> q;
AC[0].fail=0;
for(int i=0;i<N_KIND;++i){
if(AC[0].son[i]){
AC[AC[0].son[i]].fail=0;
q.push(AC[0].son[i]);
}
}
while(!q.empty()){
int u=q.front(); q.pop();
for(int i=0;i<N_KIND;++i){
if(AC[u].son[i]){
AC[AC[u].son[i]].fail=AC[AC[u].fail].son[i];
q.push(AC[u].son[i]);
}
else
AC[u].son[i]=AC[AC[u].fail].son[i];
}
}
}
inline void Match(const char str[]){
int len=strlen(str+1),p=0;
for(int i=1;i<=len;++i){
int ch=str[i]-'a';
p=AC[p].son[ch];
for(int tmp=p;tmp;tmp=AC[tmp].fail)
a[AC[tmp].end].times++;
}
}
笔者太弱没有小扩展
反正照理说 \(NOIp\) 不考
花花在上,罪过罪过
Manacher
喵的,终于要写完了,感觉啥也没写。。。
干啥子用的:
\(O(N)\) 时间内找出最长回文串啥的
怎么写
其实马拉车也是对暴力算法的一个优化
首先有三个变量:\(mid,MaxRight,p[N]\)
分别表示目前回文串右段的最远的中点,最远右段的位置,以当前这个点为中心最长的回文半径。
首先预处理:把字符之间填入无用字符比如 '#',
注意首尾符号要不同,那么答案就是 \(max_{i=1}^{n} p[i]-1\)
为什么呢,可以参考插入了无用字符
马拉车就是通过\(MaxRight\) 和 \(mid\) 来确定部分的p
那么我们就可以发现:如果当前的 \(i\) 在 \(mid- MaxRight\) 之间:
那么设关于 \(mid\) 的对称点是 \(j\)。
可以分两种情况讨论:
- j-p[j]>MaxRight的对称点
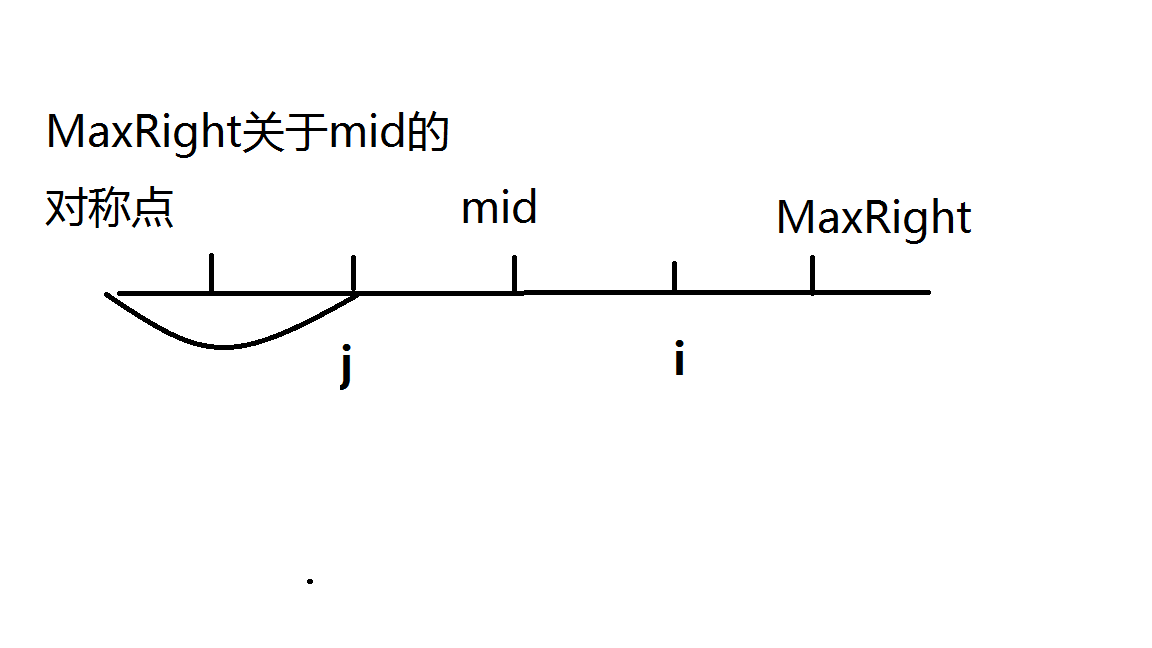
那么肯定p[i]我们能确定的最多到MaxRight,剩下的暴力跳。
- 不然
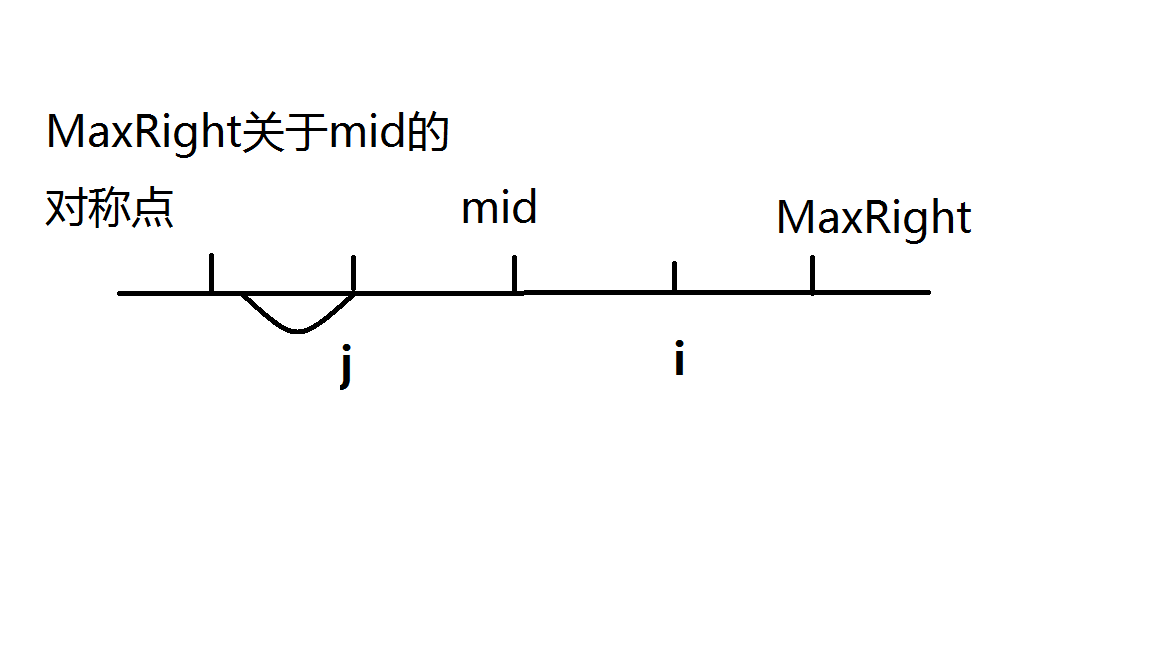
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,ans;
const int N=11000005;
char a[N],s[N<<1];
int p[N<<1];
inline void read(){
m=0;char ch=getchar();
while(!isalpha(ch)) ch=getchar();
while( isalpha(ch)) a[++m]=ch,ch=getchar();
}
int main(){
read();
s[0]='~';
s[1]='#';
n=1;
for(int i=1;i<=m;++i){
s[++n]=a[i];
s[++n]='#';
}
int maxright=0,mid=0;
for(int i=1;i<=n;++i){
if(i<maxright)
p[i]=min(p[(mid<<1)-i],maxright-i);
else p[i]=1;
while(s[i-p[i]]==s[i+p[i]]) p[i]++;
if(p[i]+i>maxright){
maxright=p[i]+i;
mid=i;
}
ans=max(ans,p[i]-1);
}
printf("%d\n",ans);
return 0;
}
完结撒花~~


