NOI导刊2010提高（06） 黑匣子
题目描述
Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。
命令只有两种：
ADD(x):把x元素放进BlackBox;
GET:i加1，然后输出Blackhox中第i小的数。
记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：
我们来演示一下一个有11个命令的命令串。（如下图所示）
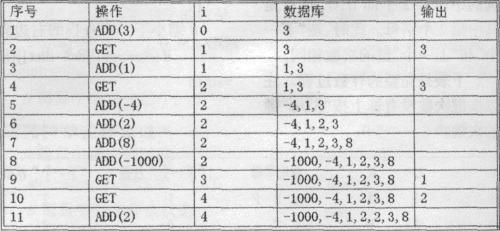
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：
1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。
2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。
输入输出格式
输入格式：第一行，两个整数，M，N。
第二行，M个整数，表示A(l)
……A(M)。
第三行，N个整数，表示u(l)
…u(N)。
输出格式：输出Black Box根据命令串所得出的输出串，一个数字一行。
输入输出样例
说明
对于30%的数据，M≤10000;
对于50%的数据，M≤100000：
对于100%的数据，M≤200000。
思路
平衡树；
代码实现
1 #include<cstdio> 2 #include<algorithm> 3 const int maxn=2e5+10; 4 int rt,ts; 5 int t[maxn],sz[maxn],num[maxn]; 6 int f[maxn],s[maxn][2]; 7 void rot(int x){ 8 int y=f[x],z=f[y],l,r; 9 l=s[y][0]==x?0:1,r=l^1; 10 if(y!=rt) s[z][s[z][1]==y]=x; 11 f[x]=z,f[y]=x,f[s[x][r]]=s[x][r]!=0?y:0; 12 s[y][l]=s[x][r],s[x][r]=y; 13 sz[y]=sz[s[y][0]]+sz[s[y][1]]+num[y]; 14 sz[x]=sz[s[x][0]]+sz[s[x][1]]+num[x]; 15 } 16 void splay(int x){ 17 int y,z; 18 while(x!=rt){ 19 y=f[x],z=f[y]; 20 if(y==rt) rot(x),rt=x; 21 else{ 22 rot((s[z][0]==y)==(s[y][0]==x)?y:x),rot(x); 23 if(z==rt) rt=x; 24 } 25 } 26 } 27 void ins(int k,int x){ 28 int fa=0; 29 while(k&&t[k]!=x) fa=k,++sz[k],k=s[k][x>t[k]]; 30 if(t[k]==x) num[k]++,sz[k]++; 31 else{ 32 k=s[fa][x>t[fa]]=++ts; 33 t[k]=x,sz[k]=1,f[k]=fa,num[k]=1; 34 } 35 splay(k); 36 } 37 void del(int k,int x){ 38 while(t[k]!=x) --sz[k],k=s[k][x>t[k]]; 39 num[k]--,sz[k]--; 40 splay(k); 41 if(!num[k]){ 42 rt=x=s[k][0]; 43 while(s[x][1]) sz[x]+=sz[s[k][1]],x=s[x][1]; 44 sz[x]+=sz[s[k][1]],s[x][1]=s[k][1],f[s[k][1]]=x; 45 } 46 } 47 int search(int k,int x){ 48 if(x<=sz[s[k][0]]) return search(s[k][0],x); 49 if(x<=sz[s[k][0]]+num[k]) return t[k]; 50 return search(s[k][1],x-sz[s[k][0]]-num[k]); 51 } 52 int n,m,x,y=1,ans=1; 53 int p[maxn]; 54 int main(){ 55 rt=++ts,t[rt]=2e9+10,sz[rt]=1,num[rt]=1,ins(rt,-2e9-10); 56 scanf("%d%d",&n,&m); 57 for(int i=1;i<=n;i++) scanf("%d",&p[i]); 58 for(int i=1;i<=m;i++){ 59 scanf("%d",&x); 60 while(y<=x) ins(rt,p[y]),y++; 61 printf("%d\n",search(rt,++ans)); 62 } 63 return 0; 64 }
