[Heoi2013]Segment
Time Limit: 40 Sec Memory Limit: 256 MB
Description
要求在平面直角坐标系下维护两个操作：
1.在平面上加入一条线段。记第i条被插入的线段的标号为i。
2.给定一个数k,询问与直线 x = k相交的线段中，交点最靠上的线段的编号。
Input
第一行一个整数n，表示共n 个操作。
接下来n行，每行第一个数为0或1。
若该数为 0，则后面跟着一个正整数 k，表示询问与直线
x = ((k +lastans–1)%39989+1)相交的线段中交点（包括在端点相交的情形）最靠上的线段的编号，其中%表示取余。若某条线段为直线的一部分，则视作直线与线段交于该线段y坐标最大处。若有多条线段符合要求，输出编号最小的线段的编号。
若该数为 1，则后面跟着四个正整数 x0, y0, x 1, y 1，表示插入一条两个端点为
((x0+lastans-1)%39989+1,(y0+lastans-1)%10^9+1)和((x
1+lastans-1)%39989+1,(y1+lastans-1)%10^9+1) 的线段。
其中lastans为上一次询问的答案。初始时lastans=0。
Output
对于每个 0操作，输出一行，包含一个正整数，表示交点最靠上的线段的编号。若不存在与直线相交的线段，答案为0。
Sample Input
6
1 8 5 10 8
1 6 7 2 6
0 2
0 9
1 4 7 6 7
0 5
1 8 5 10 8
1 6 7 2 6
0 2
0 9
1 4 7 6 7
0 5
Sample Output
2
0 3
0 3
HINT
对于100%的数据，1 ≤ n ≤ 10^5 , 1 ≤ k, x0, x1 ≤ 39989, 1 ≤ y0 ≤ y1 ≤ 10^9。
思路
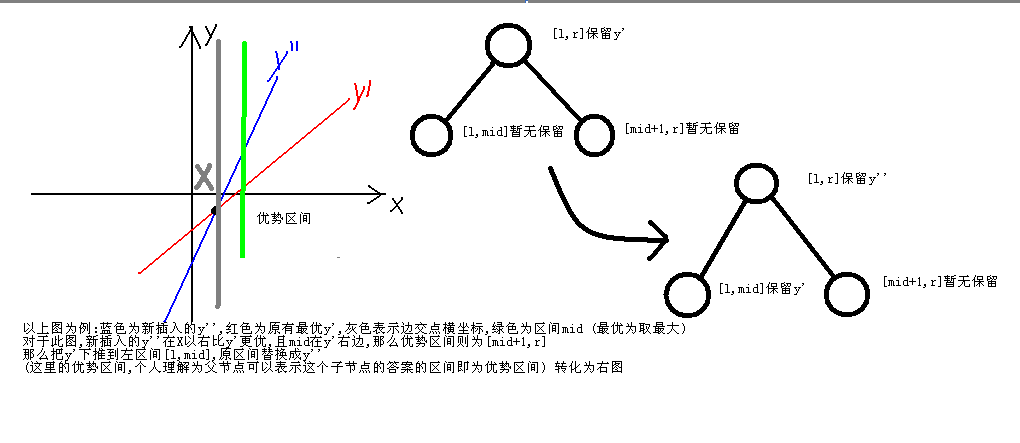
代码实现
1 #include<cstdio> 2 const int mod2=1e9; 3 const int mod1=39989; 4 const int maxn=4e4+10; 5 const double eps=1e-9; 6 inline int max_(int x,int y){return x>y?x:y;} 7 inline void swap_(int&x,int&y){x^=y,y^=x,x^=y;} 8 inline int dcmp(double x){return (x>eps)-(x<-eps);} 9 int n,m=0,lastans=0; 10 int opt,x,x0,y0,x1,y1; 11 int a[maxn],id[maxn]; 12 int L,R,idx; 13 double K,B; 14 struct node{ 15 int id; 16 double k,b; 17 bool v; 18 }t[maxn<<2]; 19 void solve(int k,int l,int r){ 20 if(t[k].v==0){ 21 t[k].k=K,t[k].b=B; 22 t[k].v=1,t[k].id=idx; 23 return; 24 } 25 double y0,y1,y2,y3; 26 y0=t[k].k*l+t[k].b,y1=K*l+B; 27 y2=t[k].k*r+t[k].b,y3=K*r+B; 28 if(dcmp(y1-y0)>0&&dcmp(y3-y2)>0){ 29 if(dcmp(K-t[k].k)==0&&dcmp(B-t[k].b)==0) return; 30 t[k].k=K,t[k].b=B,t[k].id=idx; 31 return; 32 } 33 if(dcmp(y1-y0)<=0&&dcmp(y3-y2)<=0) return; 34 int mid=l+r>>1,ls=k<<1,rs=ls|1; 35 solve(ls,l,mid),solve(rs,mid+1,r); 36 } 37 void ins(int k,int l,int r){ 38 if(L<=l&&r<=R){ 39 solve(k,l,r); 40 return; 41 } 42 int mid=l+r>>1,ls=k<<1,rs=ls|1; 43 if(L<=mid) ins(ls,l,mid); 44 if(R>mid) ins(rs,mid+1,r); 45 } 46 void ins(int x0,int x1,int y0,int y1,int num){ 47 L=x0,R=x1,idx=num; 48 K=(0.0+y1-y0)/(0.0+x1-x0),B=y0-x0*K; 49 ins(1,1,maxn); 50 } 51 int aid; 52 double ans; 53 void query(int k,int l,int r,int x){ 54 double y=t[k].k*x+t[k].b; 55 if(dcmp(y-ans)==1||(dcmp(y-ans)==0&&t[k].id<aid)) ans=y,aid=t[k].id; 56 if(l==r) return; 57 int mid=l+r>>1,ls=k<<1,rs=ls|1; 58 if(x<=mid) query(ls,l,mid,x); 59 else query(rs,mid+1,r,x); 60 } 61 int main(){ 62 scanf("%d",&n); 63 while(n--){ 64 scanf("%d",&opt); 65 if(opt==0){ 66 scanf("%d",&x); 67 x=(x+lastans-1)%mod1+1; 68 ans=aid=0; 69 query(1,1,maxn,x); 70 if(ans<a[x]||(ans==a[x]&&id[x]<aid)) aid=id[x]; 71 printf("%d\n",lastans=aid); 72 } 73 if(opt==1){ 74 scanf("%d%d%d%d",&x0,&y0,&x1,&y1),m++; 75 x0=(x0+lastans-1)%mod1+1,y0=(y0+lastans-1)%mod2+1; 76 x1=(x1+lastans-1)%mod1+1,y1=(y1+lastans-1)%mod2+1; 77 if(x0>x1) swap_(x0,x1),swap_(y0,y1); 78 if(x0==x1){if(max_(y0,y1)>a[x0]) a[x0]=max_(y0,y1),id[x0]=m;} 79 else ins(x0,x1,y0,y1,m); 80 } 81 } 82 return 0; 83 }
