【模板】最近公共祖先（LCA）
题目描述
如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。
输入输出格式
输入格式：
第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。
接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。
接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。
输出格式：
输出包含M行，每行包含一个正整数，依次为每一个询问的结果。
输入输出样例
输入样例#1：
5 5 4 3 1 2 4 5 1 1 4 2 4 3 2 3 5 1 2 4 5
输出样例#1：
4 4 1 4 4
说明
时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=10，M<=10
对于70%的数据：N<=10000，M<=10000
对于100%的数据：N<=500000，M<=500000
样例说明：
该树结构如下：
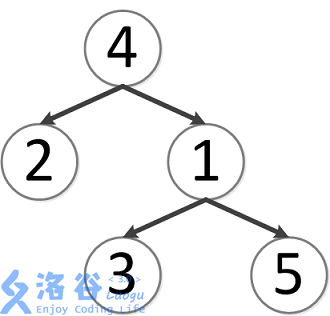
第一次询问：2、4的最近公共祖先，故为4。
第二次询问：3、2的最近公共祖先，故为4。
第三次询问：3、5的最近公共祖先，故为1。
第四次询问：1、2的最近公共祖先，故为4。
第五次询问：4、5的最近公共祖先，故为4。
故输出依次为4、4、1、4、4。
其实嘛，LCA倍增版就是把祖上十八辈都存下来（当然只存足够二的祖先）。
代码实现：
1 #include<cstdio> 2 #define maxn 500010 3 int n,m,s; 4 int a,b; 5 int d[maxn],q[maxn],f[maxn][32]; 6 int h[maxn],hs; 7 struct edge{int s,n;}e[maxn<<1]; 8 void dfs(int k,int deep){ 9 d[k]=deep,q[deep]=k; 10 int nd=deep+1; 11 for(int i=h[k];i;i=e[i].n) 12 if(!d[e[i].s]){ 13 for(int j=1,k=0;nd>j;j*=2,k++) f[e[i].s][k]=q[nd-j]; 14 dfs(e[i].s,nd); 15 } 16 } 17 int main(){ 18 scanf("%d%d%d",&n,&m,&s); 19 for(int i=1;i<n;i++){ 20 scanf("%d%d",&a,&b); 21 e[++hs]=(edge){b,h[a]},h[a]=hs; 22 e[++hs]=(edge){a,h[b]},h[b]=hs; 23 } 24 dfs(s,1); 25 for(int i=1;i<=m;i++){ 26 scanf("%d%d",&a,&b); 27 while(a!=b){ 28 if(d[a]==d[b]) for(int j=0;;j++) if(f[a][j+1]==f[b][j+1]){a=f[a][j],b=f[b][j];break;} 29 if(d[a]>d[b]) for(int j=0;;j++) if(d[f[a][j+1]]<d[b]){a=f[a][j];break;} 30 if(d[a]<d[b]) for(int j=0;;j++) if(d[f[b][j+1]]<d[a]){b=f[b][j];break;} 31 } 32 printf("%d\n",a); 33 } 34 return 0; 35 }
题目来源：洛谷
