【模板】网络最大流
题目描述
如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。
输入输出格式
输入格式：
第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）
输出格式：
一行，包含一个正整数，即为该网络的最大流。
输入输出样例
输入样例#1：
4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40
输出样例#1：
50
说明
时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=10，M<=25
对于70%的数据：N<=200，M<=1000
对于100%的数据：N<=10000，M<=100000
样例说明：
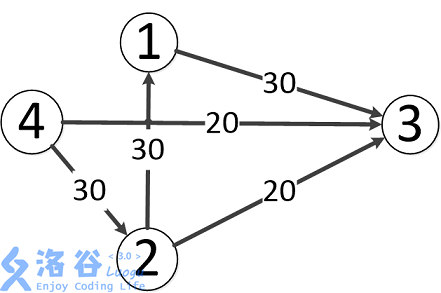
题目中存在3条路径：
4-->2-->3，该路线可通过20的流量
4-->3，可通过20的流量
4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）
故流量总计20+20+10=50。输出50。
思路：Dinic
首先建边，我直接把反向边建好了；
边的结构体里依次存着{汇点，源点下一条边的位置，边权，反向边位置}；
然后进入Dinic；
先bfs一遍，给每个店一个d（即从s点跑一个生成树的点深度）；
然后只要能到达汇点，即d[t]!=0;
就找一遍增广路。
可能因为我一开始就把反向边建好了，所以有点慢。
为了模板的优秀与通用性，又敲了个更优美也更优异的。
代码实现：
1 #include<cstdio> 2 #include<cstring> 3 int n,m,s,t,ans,d[10010]; 4 int a,b,c; 5 int h[10010],hs,head,tail; 6 struct edge{int s,n,v,r;}e[200010]; 7 struct queue{int s,d;}q[10010]; 8 int min(int x,int y){return x<y?x:y;} 9 void bfs(int s,int t){ 10 memset(d,0,sizeof(d)); 11 head=tail=0; 12 q[head++]=(queue){s,1},d[s]=1; 13 while(head>tail){ 14 a=q[tail].s,b=q[tail++].d; 15 for(int i=h[a];i;i=e[i].n) if(!d[e[i].s]&&e[i].v){ 16 q[head++]=(queue){e[i].s,b+1}; 17 d[e[i].s]=b+1; 18 } 19 } 20 } 21 int ap(int k,int t,int v){ 22 if(k==t) return v; 23 int act=0; 24 for(int i=h[k];i;i=e[i].n) if(e[i].v&&d[e[i].s]==d[k]+1){ 25 int ret=ap(e[i].s,t,min(v-act,e[i].v)); 26 if(ret) e[i].v-=ret,e[e[i].r].v+=ret,act+=ret; 27 } 28 return act; 29 } 30 bool Dinic(int s,int t){ 31 bfs(s,t); 32 if(!d[t]) return 0; 33 ans+=ap(s,t,1000000000); 34 } 35 int main(){ 36 scanf("%d%d%d%d",&n,&m,&s,&t); 37 for(int i=1;i<=m;i++){ 38 scanf("%d%d%d",&a,&b,&c); 39 e[++hs]=(edge){b,h[a],c,hs+1},h[a]=hs; 40 e[++hs]=(edge){a,h[b],0,hs-1},h[b]=hs; 41 } 42 while(Dinic(s,t)); 43 printf("%d\n",ans); 44 return 0; 45 }
第二版 233mm：
1 #include<cstdio> 2 #include<cstring> 3 #define inf 1073741824 4 int n,m,s,t,wt; 5 int a,b,c; 6 int d[10010],q[10010],head,tail; 7 int h[10010],hs=1; 8 struct edge{int s,n,w;}e[300000]; 9 inline int min(int x,int y){return x<y?x:y;} 10 void bfs(){ 11 memset(d,0,sizeof(d)); 12 head=tail=0; 13 d[s]=1,q[head++]=s; 14 while(head>tail){ 15 a=q[tail++]; 16 for(int i=h[a];i;i=e[i].n) 17 if(!d[e[i].s]&&e[i].w){ 18 d[e[i].s]=d[a]+1; 19 if(e[i].s==t) return; 20 q[head++]=e[i].s; 21 } 22 } 23 } 24 int ap(int k,int nw){ 25 if(k==t) return nw; 26 int bw=nw; 27 for(int i=h[k];i&&bw;i=e[i].n) 28 if(e[i].w&&d[e[i].s]==d[k]+1){ 29 int dw=ap(e[i].s,min(bw,e[i].w)); 30 if(dw) e[i].w-=dw,e[i^1].w+=dw,bw-=dw; 31 else d[e[i].s]=0; 32 } 33 return nw-bw; 34 } 35 bool Dinic(){ 36 bfs(); 37 if(!d[t]) return 0; 38 wt+=ap(s,inf); 39 return 1; 40 } 41 int main(){ 42 scanf("%d%d%d%d",&n,&m,&s,&t); 43 for(int i=1;i<=m;i++){ 44 scanf("%d%d%d",&a,&b,&c); 45 e[++hs]=(edge){b,h[a],c},h[a]=hs; 46 e[++hs]=(edge){a,h[b],0},h[b]=hs; 47 } 48 while(Dinic()); 49 printf("%d\n",wt); 50 return 0; 51 }
题目来源：洛谷
