【模板】单源最短路径*
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入输出格式
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
输入输出样例
输入样例#1:
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
输出样例#1:
0 2 4 3
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15
对于40%的数据:N<=100,M<=10000
对于70%的数据:N<=1000,M<=100000
对于100%的数据:N<=10000,M<=500000
样例说明:
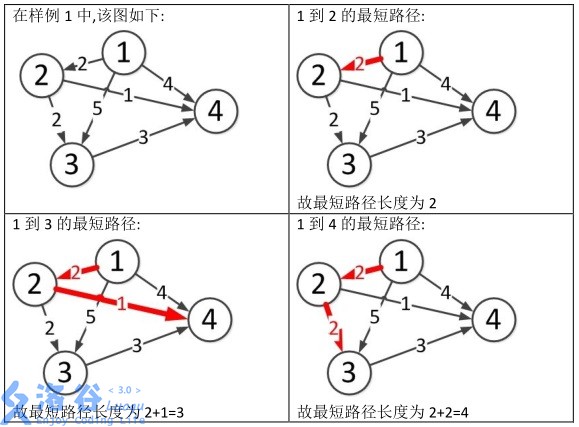
思路:SPFA or Dijkstra
此题是有向边!!!(然而我并没有被这里坑)
SPFA
初始化最短路径表;
源点入队;
取出队首点;
枚举取出点的边;
如果能松弛,就松弛,并把被松弛的点加入队列;
如此循环直到队列为空。
另外,根据2183ms的亲测,使用优先队列应该没有明显优化效果(可能更稳定了,我不太懂)。
Dijkstra
初始化最短路径表;
源点标记;
用源点的边松弛;
寻找距离最短的未被标记的点;
用这个点的边松弛;
如此循环n-1次。
虽然Dijkstra大部分时候不如SPFA快,但理论是Dijkstra更稳定。
代码实现
769ms的SPFA:
1 #include<cstdio> 2 int n,m,s,v[10010]; 3 int a,b,c; 4 int q[500010],head,tail; 5 int h[10010],hs; 6 struct edge{int s,n,v;}e[500010]; 7 inline bool rel(long long x,long long y,long long z){return y+z<x?1:0; } 8 int main(){ 9 scanf("%d%d%d",&n,&m,&s); 10 for(int i=1;i<=n;i++) if(i!=s) v[i]=2147483647; 11 for(int i=1;i<=m;i++){ 12 scanf("%d%d%d",&a,&b,&c); 13 e[++hs]=(edge){b,h[a],c}; 14 h[a]=hs; 15 } 16 q[head++]=s; 17 while(head>tail){ 18 a=q[tail++]; 19 for(int i=h[a];i;i=e[i].n){ 20 if(rel(v[e[i].s],v[a],e[i].v)){ 21 q[head++]=e[i].s; 22 v[e[i].s]=v[a]+e[i].v; 23 } 24 } 25 } 26 for(int i=1;i<=n;i++) printf("%d ",v[i]); 27 return 0; 28 }

1 #include<queue> 2 #include<cstdio> 3 using namespace std; 4 int n,m,s,v[10010]; 5 int a,b,c; 6 priority_queue <int> q; 7 int h[10010],hs; 8 struct edge{int s,n,v;}e[500010]; 9 inline bool rel(long long x,long long y,long long z){return y+z<x?1:0; } 10 int main(){ 11 scanf("%d%d%d",&n,&m,&s); 12 for(int i=1;i<=n;i++) if(i!=s) v[i]=2147483647; 13 for(int i=1;i<=m;i++){ 14 scanf("%d%d%d",&a,&b,&c); 15 e[++hs]=(edge){b,h[a],c}; 16 h[a]=hs; 17 } 18 q.push(s); 19 while(!q.empty()){ 20 a=q.top(); 21 q.pop(); 22 for(int i=h[a];i;i=e[i].n){ 23 if(rel(v[e[i].s],v[a],e[i].v)){ 24 q.push(e[i].s); 25 v[e[i].s]=v[a]+e[i].v; 26 } 27 } 28 } 29 for(int i=1;i<=n;i++) printf("%d ",v[i]); 30 return 0; 31 }
2305ms的Dijkstra:
1 #include<cstdio> 2 int n,m,s,w[10010]; 3 int a,b,c; 4 bool v[10010]; 5 int h[10010],hs; 6 struct edge{int s,n,v;}e[500010]; 7 inline bool rel(long long x,long long y,long long z){return y+z<x?1:0;} 8 int main(){ 9 scanf("%d%d%d",&n,&m,&s); 10 for(int i=1;i<=n;i++) if(i!=s) w[i]=2147483647; 11 for(int i=1;i<=m;i++){ 12 scanf("%d%d%d",&a,&b,&c); 13 e[++hs]=(edge){b,h[a],c}; 14 h[a]=hs; 15 } 16 v[s]=1; 17 for(int i=h[s];i;i=e[i].n) if(rel(w[e[i].s],0,e[i].v)) w[e[i].s]=e[i].v; 18 for(int k=1;k<n;k++){ 19 a=2147483647; 20 for(int i=1;i<=n;i++) if(!v[i]&&w[i]<a) a=w[i],b=i; 21 v[b]=1; 22 for(int i=h[b];i;i=e[i].n) if(rel(w[e[i].s],w[b],e[i].v)) w[e[i].s]=e[i].v+w[b]; 23 } 24 for(int i=1;i<=n;i++) printf("%d ",w[i]); 25 return 0; 26 }
20分的堆优化的Dijkstra(恕我无能):
1 #include<cstdio> 2 #define LL long long 3 #define maxn 10010 4 #define maxm 500010 5 #define inf 2147483647 6 int n,m,q,w[maxn],in[maxn]; 7 int a,b,c,l,r; 8 int p[maxn],ps,top; 9 bool v[maxn]; 10 struct edge{int s,n,v;}e[maxm]; 11 struct heap{int s,v;}h[maxm]; 12 inline void add(int x,int y,int z){e[++ps]=(edge){y,p[x],z},p[x]=ps;} 13 inline LL min(LL x,LL y,LL z){return x<y+z?x:y+z;} 14 void swap(int x,int y,int xx,int yy){ 15 h[0]=(heap){h[x].s,h[x].v}; 16 h[x]=(heap){h[y].s,h[y].v}; 17 h[y]=(heap){h[0].s,h[0].v}; 18 in[xx]=y;in[yy]=x; 19 } 20 void push(int x,int y,int z){ 21 h[z]=(heap){x,y},in[x]=z; 22 while(in[x]>1){ 23 if(h[in[x]].v<h[in[x]>>1].v) swap(in[x],in[x]>>1,x,h[in[x]>>1].s); 24 else break; 25 } 26 } 27 int pop(){ 28 int ret=h[1].s; 29 h[1]=(heap){h[top].s,h[top--].v}; 30 int x=h[1].s,z; 31 in[h[1].s]=1; 32 while(in[x]<=top){ 33 l=in[x]<<1,r=l+1; 34 if(h[l].v<h[r].v) z=l; 35 else z=r; 36 if(h[z].v<h[in[x]].v) swap(in[x],z,x,h[z].s); 37 else break; 38 } 39 return ret; 40 } 41 int main(){ 42 scanf("%d%d%d",&n,&m,&q); 43 for(int i=1;i<=n;i++) if(i!=q) w[i]=inf; 44 for(int i=1;i<=m;i++){ 45 scanf("%d%d%d",&a,&b,&c); 46 add(a,b,c); 47 } 48 for(int k=0;k<n;k++){ 49 if(k) q=pop(); 50 v[q]=1; 51 for(int i=p[q];i;i=e[i].n){ 52 a=e[i].s,b=min(w[a],w[q],e[i].v); 53 if(b<w[a]){ 54 w[a]=b; 55 if(in[a]) push(a,w[a],in[a]); 56 else push(a,w[a],++top); 57 } 58 } 59 } 60 for(int i=1;i<=n;i++) printf("%d ",w[i]); 61 return 0; 62 }
感觉洛谷的板子题都好厉害。
题目来源:洛谷




 浙公网安备 33010602011771号
浙公网安备 33010602011771号