F - 树状数组 2

F - 树状数组 2

原题链接

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 \(x\)；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 \(N\)、\(M\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 \(N\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 $i $ 项的初始值。

接下来 \(M\) 行每行包含 \(2\) 或 \(4\)个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)；

操作 \(2\)： 格式：2 x 含义：输出第 \(x\) 个数的值。

输出格式

输出包含若干行整数，即为所有操作 \(2\) 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

6
10

提示

样例 1 解释：

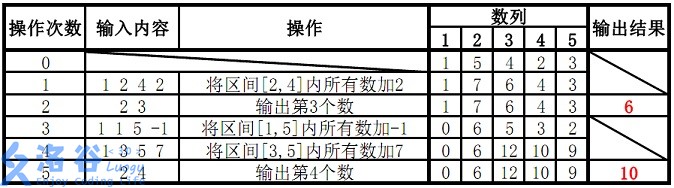
故输出结果为 6、10。

---

数据规模与约定

对于 \(30\%\) 的数据：\(N\le8\)，\(M\le10\)；

对于 \(70\%\) 的数据：\(N\le 10000\)，\(M\le10000\)；

对于 \(100\%\) 的数据：\(1 \leq N, M\le 500000\)，\(1 \leq x, y \leq n\)，保证任意时刻序列中任意元素的绝对值都不大于 \(2^{30}\)。

思路

在树状数组1中我们可以得知

• 单点修改，区间查询（区间和）
  对原数组进行单点修改，对区间和进行树状数组维护

利用差分和前缀和我们可以推导出

• 区间修改（差分），单点查询
  原数组 = 差分的前缀和数组
  对差分数组进行单点修改实现区间修改，对差分的前缀和数组（即原数组）进行树状数组维护实现单点查询

代码

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;

#define X first
#define Y second

typedef pair<int,int> pii;
typedef long long LL;
const char nl = '\n';
const int N = 5e5+10;
const int M = 2e5+10;
int n,m;
LL a[N],d,b[N];

int lowbit(int x){
	return x & -x;
}

void add(int k,int x){
	while(k <= n){
		b[k] += x;
		k += lowbit(k);
	}
}

LL getsum(int l,int r){
	l --;
	LL s1 = 0;
	while(l){
		s1 += b[l];
		l -= lowbit(l);
	}
	LL s2 = 0;
	while(r){
		s2 += b[r];
		r -= lowbit(r);
	}
	return s2 -s1;
}
void solve(){
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ){
		cin >> a[i];		//原数组
		d = a[i] - a[i-1];	//差分数组
		add(i,d);	//对差分数组的前缀和进行树状数组维护
	}
	while(m --){
		int op;
		cin >> op;
		if(op == 1){
			int l,r,x;
			cin >> l >> r >> x;
			add(l,x);	//差分
			add(r+1,-x);	//差分
		}
		else{	//输出s[k]差分数组(1,k)的和
			int k;
			cin >> k;
			cout << getsum(1,k) << nl;	
		}
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);

	solve();
}