E - 树状数组 1
E - 树状数组 1
题目描述
如题，已知一个数列，你需要进行下面两种操作：
-
将某一个数加上 \(x\)
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 \(n,m\)，分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 个整数，表示一个操作，具体如下：
-
1 x k含义：将第 \(x\) 个数加上 \(k\) -
2 x y含义：输出区间 \([x,y]\) 内每个数的和
输出格式
输出包含若干行整数，即为所有操作 \(2\) 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出 #1
14
16
提示
【数据范围】
对于 \(30\%\) 的数据，\(1 \le n \le 8\)，\(1\le m \le 10\)；
对于 \(70\%\) 的数据，\(1\le n,m \le 10^4\)；
对于 \(100\%\) 的数据，\(1\le n,m \le 5\times 10^5\)。
数据保证对于任意时刻，\(a\) 的任意子区间（包括长度为 \(1\) 和 \(n\) 的子区间）和均在 \([-2^{31}, 2^{31})\) 范围内。
样例说明：
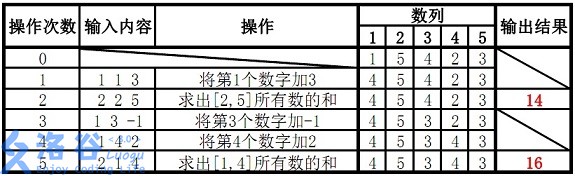
故输出结果14、16
题意
已知一个数列，你需要进行下面两种操作：
-
将某一个数加上 \(x\)
-
求出某区间每一个数的和
树状数组解决的基本问题
在一个序列中
\(①\)修改某一个数(\(logn\))
\(②\)快速求前缀和(\(logn\))
思考：朴素算法如何实现？
\(①\)直接使用数组存每一个数，那么我们求前缀和的复杂度就是\(O(n)\)，修改一个数的复杂度就是\(O(1)\)
\(②\)使用前缀和数组，那么我们求前缀和的复杂度就是\(O(1)\)，修改一个数的复杂度就是\(O(n)\)
“鱼和熊掌不可兼得”，如果第一个操作很快，那么第二个操作就会变得很慢
假设我们有m次询问，要看最坏的情况，那么这两种方式复杂度都到达了\(O(nm)\)的级别
通过树状数组，我们可以把两种操作都做到\(logn\)级别，也就是\(O(mlogn)\)，效率得到了很大的提升
lowbit函数(前置知识)
定义一个函数\(f=lowbit(x)\)，这个函数的值是\(x\)的二进制表达式中只保留最低位\(1\)得到的十进制数
比如:
那么\(lowbit(6)\)就等于\(2\)，因为\((110)_2\)中最低位（就是从右往左数的第二位）对应的数是\((10)_2=(2)_{10}\)
所以假设一个数的二进制最低位的1在从右往左数的第k位，那么它的lowbit值就是
int lowbit(int x){
return x & -x;
}
原理：
根据计算机补码的性质。
补码就是原码的反码加一
如：
反码：
加一：
可以发现变为反码后 x 与反码数字位每一位都不同， 当反码加1，反码会逢1一直进位直到遇到0，且这个0变成了1，所以这个数最后面构造了一个 100… 串。 只有一个\(1\),因此进行&运算后除了该位上存在\(1\)，其他位都是\(0\)（反码的最低位\(0\)变成\(1\)，与反码取反前的原码相同都是\(1\)）,进而得到二进制表达式中只保留最低位\(1\)得到的十进制数
树状数组的定义
树状数组是一种维护前缀和的数据结构，可以实现 \(O(\log{n})\)查询一个前缀的和，\(O(\log{n})\)对原数列的一个位置进行修改。
- 与前缀和相同的是，树状数组使用与原数列大小相同的数组即可维护
- 与前缀和不同的是，树状数组的一个位置 i 存储的是从 i 开始，（包括 i）向前\(t_i\)个元素的和
\(t_i\)就是最大的可以整除 \(i\) 的\(2\)的幂（通过上述\(lowbit\)函数可以得到）
树状数组的性质
设树状数组为b
性质1：有上述定义得到$b[k] = \sum_{k-lowbit(k)+1}^{k} $
性质2：父节点 \(b[dad] = b[k] + lowbit(k)\)
(上为树状数组b,下为原数组a)
树状数组单点修改
根据性质2可以改造出对树状数组单点修改的函数
\(add(int \ k,int \ x)\)功能：下标为k的增加x
void add(int k,int x){
while(k <= n){ //不能超范围
b[k] += x;
k += lowbit(k); //维护父节点
}
}
注意：空数组本身就是一个树状数组(和均为0),因此原数组输入数据维护树状数组b时可以直接\(add(i,a_i)\)
树状数组区间查询
作差求lr的区间和:sum[1r] - sum[1~l-1]
根据性质1：
LL getsum(int l,int r){
l --;
LL s1 = 0;
while(l){
s1 += b[l];
l -= lowbit(l);
}
LL s2 = 0;
while(r){
s2 += b[r];
r -= lowbit(r);
}
return s2 - s1;
}
最终代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
#define X first
#define Y second
typedef pair<int,int> pii;
typedef long long LL;
const char nl = '\n';
const int N = 1e6+10;
const int M = 2e5+10;
int n,m;
int a,b[N];
int lowbit(int x){
return x & -x;
}
void add(int k,int x){
while(k <= n){
b[k] += x;
k += lowbit(k);
}
}
LL getsum(int l,int r){
l --;
LL s1 = 0;
while(l){
s1 += b[l];
l -= lowbit(l);
}
LL s2 = 0;
while(r){
s2 += b[r];
r -= lowbit(r);
}
return s2 - s1;
}
void solve(){
cin >> n >> m;
for(int i = 1; i <= n; i ++ ){
cin >> a;
add(i,a);
}
while(m -- ){
int op;
cin >> op;
if(op == 1){
int k,x;
cin >> k >> x;
add(k,x);
}
else{
int l,r;
cin >> l >> r;
cout << getsum(l,r) << nl;
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
solve();
}
