HRBUST 1214 方格取数

题目链接：HRBUST 1214 方格取数

题目大意：

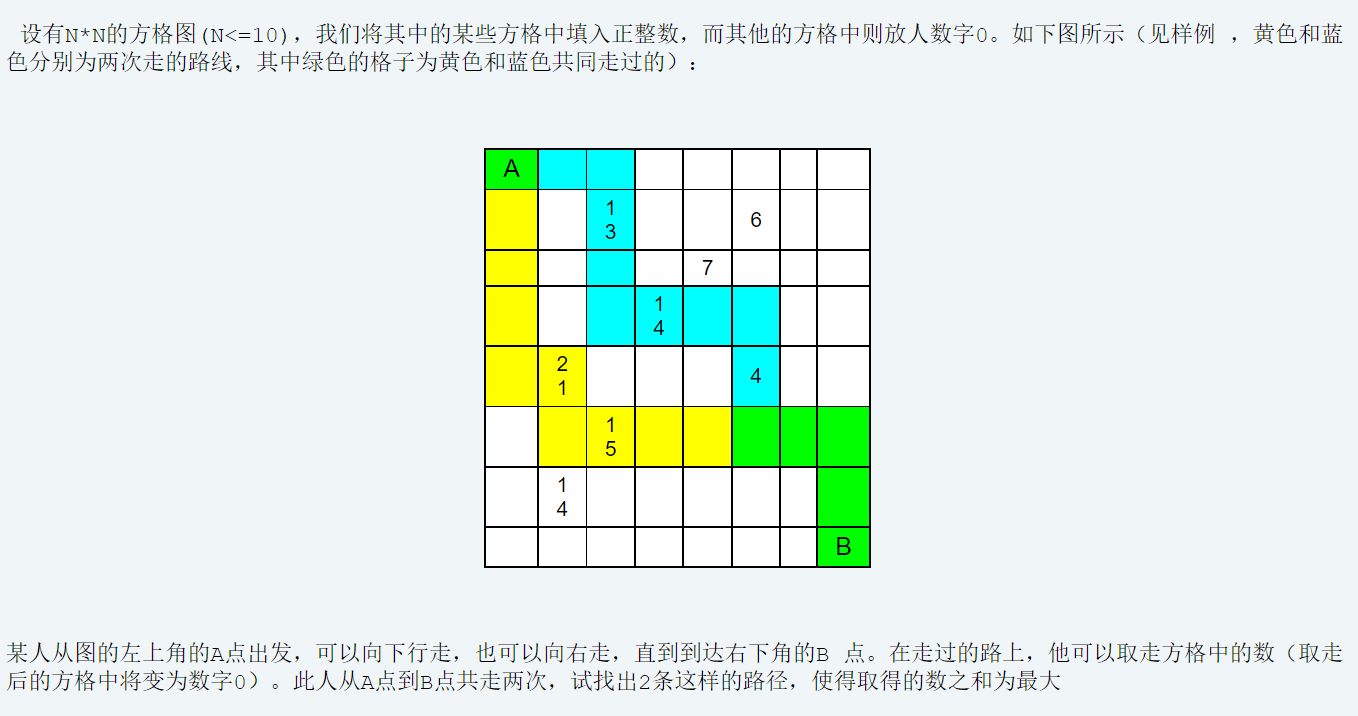
题解：
设\(dp[i][j][x][y]\)表示第一次走到\(i\)行\(j\)列，第二次走到\(x\)行\(y\)列时能取的数的最大和。
状态转移方程：

\[dp[i][j][x][y]=max\{dp[i-1][j][x-1][y], dp[i][j-1][x-1][y],dp[i-1][j][x][y-1], dp[i][j-1][x][y-1]\}+num[i][j]+num[x][y] \]

对于\(num[i][j],num[x][y]\)两点重合时只加一项。
答案为\(dp[n][n][n][n]\)。

#include <cstring>
#include <iostream>
using namespace std;

int dp[11][11][11][11], num[11][11], n;

int max_4(int a, int b, int c, int d) { return max(a, max(b, max(c, d))); }

int main() {
    while (cin >> n) {
        memset(dp, 0, sizeof(dp));
        memset(num, 0, sizeof(num));
        int a, b, c;
        while (cin >> a >> b >> c && (a || b || c)) {
            num[a][b] = c;
        }
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                for (int x = 1; x <= n; ++x) {
                    for (int y = 1; y <= n; ++y) {
                        dp[i][j][x][y] = max_4( dp[i - 1][j][x - 1][y], dp[i][j - 1][x - 1][y], dp[i - 1][j][x][y - 1], dp[i][j - 1][x][y - 1]);
                        if (i == x && j == y) {
                            dp[i][j][x][y] += num[i][j];
                        } else {
                            dp[i][j][x][y] += num[i][j] + num[x][y];
                        }
                    }
                }
            }
        }
        cout << dp[n][n][n][n] << endl;
    }
    return 0;
}