动态规划的各种模型<三>
本篇主要讲解树形 DP 与基环树 DP 。
配合文章右上角目录食用更佳。
树形DP
一类在树上的动态规划。
由于树的特殊性质,我们一般会使用 DFS序 来完成 DP,或者在树的topo序列上 DP。
其划分状态的标准也多与子节点的性质有关。
树的最长直径
给定一棵树,树中包含 \(n\) 个结点(编号 \(1~n\))和 \(n−1\) 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 \(n\)。
接下来 \(n−1\) 行,每行包含三个整数 \(a_i,b_i,c_i\),表示点 \(a_i\) 和 \(b_i\) 之间存在一条权值为 \(c_i\) 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
\(1≤n≤10000, 1≤a_i,b_i≤n, −10^5≤c_i≤10^5\)
输入样例:
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22
解析
求树的直径。
不带权值的树的直径有其他的定理可以求,但是这里带权,并且正负都有。
看一下树的直径究竟是什么样子的。
由于这是一棵无根树,并且树的直径不随根节点的变化而改变,我们可以随便拿一个节点做根节点:

容易发现,一条红色路径可以被分为两条相似的蓝色路径。而我们要是一条红色路径最长,就要使得分解出来的两条蓝色路径最长。我们可以记录一下到某个节点子树内的节点到它的路径的最长值 \(d\) 和次长值 \(d^{\prime}\) ,加起来就是这个子树内的直径。
下面我们关注某一个节点子树内的 \(d\) 怎么求。

观察这个图,我们可以发现轻易发现,最长值能够很轻易地从子节点转移过来,我们考虑进行 DP 分析:
- 设: \(d_i\) 为在 \(i\) 点的子树中的所有节点到 \(i\) 点的所有简单路径的最长距离。
寻找最后一个不同点,即子节点及子树不同,按照这个来划分状态集合。

从定义出发,我们要找到 \(i\) 的最长路径,就可以找到 \(i\) 的子节点 \(j\) 的最长路径,然后加上 \((i,j)\) 的权值,打擂台记录最大值。
次长值在打擂台的时候记录一下被打下来的值即可。
算完之后所有节点 \(d\) 值的最大值就是树的直径,我们可以在 DFS 的时候即时更新答案。
code
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n;
int head[N],ver[N<<1],nxt[N<<1],edg[N<<1],tot=0;
void add(int x,int y,int z)
{
ver[++tot]=y; edg[tot]=z; nxt[tot]=head[x]; head[x]=tot;
}
int ans=0;
int dfs(int x,int f)
{
int dis=0,d1=0,d2=0;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==f) continue;
int d=dfs(y,x)+edg[i];
if(d>d1) d2=d1,d1=d;//打擂台
else if(d>d2) d2=d;
}
ans=max(d1+d2,ans);
return d1;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<n;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dfs(1,1);
printf("%d",ans);
}
数字转换
如果一个数 \(x\) 的约数之和 \(y\)(不包括他本身)比他本身小,那么 \(x\) 可以变成 \(y\),\(y\) 也可以变成 \(x\)。
例如,\(4\) 可以变为 \(3\),\(1\) 可以变为 \(7\)。
限定所有数字变换在不超过其本身的正整数范围内进行(如 \(20\) 不能变成 \(22\),即使给出的 \(n>22\) ),求不断进行数字变换且不出现重复数字的最多变换步数。
输入格式
输入一个正整数 \(n\)。
输出格式
输出不断进行数字变换且不出现重复数字的最多变换步数。
数据范围
\(1≤n≤50000\)
输入样例:
7
输出样例:
3
样例解释
一种方案为:\(4→3→1→7\)。
解析
很容易知道的是,一个数的约数和是固定的。又因为变换不能出现重复的数字,所以我们能够联想到树与树之间的变换关系是一个无向无环图,也就是一棵无根树。
而最长的变换关系链,即是树的直径。
树的直径 \(O(n)\) DP 即可,本题数据范围小,可以直接 \(O(n\sqrt n)\) 预处理变换关系。
code:
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int n;
int head[N],ver[N<<1],nxt[N<<1],tot=0;
void add(int x,int y)
{
ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot;
ver[++tot]=x; nxt[tot]=head[y]; head[y]=tot;
}
int fa[N],rk[N];
void init()
{
for(int i=0;i<N;i++) fa[i]=i,rk[i]=0;
}
int find(int x)//并查集维护联通
{
int x_root=x;
while(x_root!=fa[x_root])
x_root=fa[x_root];
while(x!=x_root)
{
int tmp=fa[x];
fa[x]=x_root;x=tmp;
}
return x_root;
}
int union_(int x,int y)
{
int x_root=find(x);
int y_root=find(y);
if(x_root==y_root) return 0;
if(rk[x_root]>rk[y_root]) fa[y_root]=x_root;
else if(rk[x_root]<rk[y_root]) fa[x_root]=y_root;
else fa[y_root]=x_root,rk[x_root]++;
return 1;
}
int ans=0,vis[N];
int dfs(int x,int f)
{
int d1=0,d2=0;
vis[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==f) continue;
int d=dfs(y,x)+1;
if(d>=d1) d2=d1,d1=d;
else if(d>d2) d2=d;
}
ans=max(ans,d1+d2);
return d1;
}
int main()
{
// freopen("tt.txt","w",stdout);
scanf("%d",&n);
init();
for(int i=2;i<=n;i++)
{
int ans=1;//先把 1 加进去
for(int j=2;j*j<=i;j++)//计算约数和
{
if(i%j==0)
{
ans+=j;
if(j*j!=i) ans+=i/j;
}
}
if(union_(i,ans)&&ans<=i) add(i,ans)/*,printf("%d %d\n",i,ans)*/;//记得判重
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs(i,i);//注意,所有的转移关系组成的是一棵森林,我们要求其中树的直径最大值
printf("%d",ans);
return 0;
}
二叉苹果树
有一棵二叉苹果树,如果树枝有分叉,一定是分两叉,即没有只有一个儿子的节点。
这棵树共 \(N\) 个节点,编号为 \(1\) 至 \(N\),树根编号一定为 \(1\)。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。
这里的保留是指最终与 \(1\) 号点连通。
输入格式
第一行包含两个整数 \(N\) 和 \(Q\),分别表示树的节点数以及要保留的树枝数量。
接下来 \(N−1\) 行描述树枝信息,每行三个整数,前两个是它连接的节点的编号,第三个数是这根树枝上苹果数量。
输出格式
输出仅一行,表示最多能留住的苹果的数量。
数据范围
\(1≤Q<N≤100,
N≠1,\)
每根树枝上苹果不超过 \(30000\) 个。
输入样例:
5 2
1 3 1
1 4 10
2 3 20
3 5 20
输出样例:
21
解析
我们画一画样例的图:

观察发现,我们可以将边权下放点权,这个问题就变成了从根节点开始选连通块使得权值最大的问题。
对于某一个节点,如果我们选了它,我们就可以选其儿子节点,儿子节点又可以选儿子节点。
我们可以在选择儿子节点的时候,给它分配一个配额,这个配额是它子树中最多能选择的子节点数。它可以继续把这个配额分配给它的子节点。最终,它会返回一个价值,那就是它在分配到特定配额下的最大价值。我们可以设一个函数 \(C_i(x)\) 表示物品 \(i\) 在分配到 \(x\) 配额的情况下能拿到的最大价值。
将这些子节点看做物品,这些物品的价值随着某一个指标的变化而变化,是一种典型的 泛化物品,而选择这些物品的过程,就是 泛化物品背包 的过程。
- 泛化物品定义: 考虑一种物品,它没有固定的费用和价值,而是其价值随着分配给它的费用变化而变化。
对于一个泛化物品,可以用一个一维数组\(G_i\)表示其费用与价值的关系:当费用为\(i\)时,相对应的价值为\(G_i\)。
- 泛化物品的和:把两个物品合在一起的运算,就是枚举费用分配给两个物品,
满足:
\(G_j=max(G1_{j-k},G2_{k})(0 \leq k \leq j \leq C)\)
时间复杂度为\(O(C^2)\)。
- 对于一组成树形依赖关系的物品,我们可以将每个子树都看作一个泛化物品,那么一个子树的泛化物品就是子树根节点这件物品和它的子节点所在子树的泛化物品的和。
我们设 \(f(i,j)\) 为在 \(i\) 的子树中(不包含 \(i\) )选择 \(j\) 个节点的最大值。
对于其某个子节点 \(x\) ,我们可以得到 \(f(i,j)=\text{Max}_{k=0}^{j-1}\{f(x,k)\}\)
当然本题一个树枝就两个分叉,是一个树形背包的简化版。
#include <bits/stdc++.h>
using namespace std;
const int N=2010;
int n,q;
int head[N],ver[N],nxt[N],edg[N],tot=0;
void add(int x,int y,int z)
{
ver[++tot]=y; edg[tot]=z; nxt[tot]=head[x]; head[x]=tot;
}
int f[N][N];
void dfs(int x,int fa)
{
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==fa) continue;
dfs(y,x);
for(int j=q;j>=0;j--)
{
for(int k=0;k<j;k++)
f[x][j]=max(f[x][j],f[y][k]+f[x][j-k-1]+edg[i]);
}
}
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<n;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(b,a,c);
add(a,b,c);
}
dfs(1,1);
printf("%d",f[1][q]);
}
战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
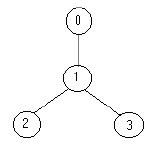
只需要放置 \(1\) 名士兵(在节点 \(1\) 处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数 \(N\),表示树的节点数目。
接下来 \(N\) 行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从 \(0\) 到 \(N−1\),每个节点的子节点数量均不超过 \(10\),每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
\(0<N≤1500\)
输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
解析
简化一下题意:给定一棵树,对树中的每条边 \((u,v)\) 至少选一个端点 \(u\) 或 \(v\),求最少要选多少点。
对于一个点的选或不选两种状态,我们可以使用黑白染色的方法来区分。那么题目的要求就是对于一条边至少有一个端点是黑点。
一个点的状态只有 \(0/1\) 两种,相邻两个点状态之间相互制约,我们可以联想到状态机模型。
- 设状态 \(f(u,k(0/1))\) 为在 \(i\) 的子树中选,且第 \(i\) 个节点选或不选( \(k=1\) 或 \(0\) )的所有选法的最小点数。
下面我们来看状态计算的问题。
与线性状态机模型不同的是,树形状态机状态转移的源头更加复杂,一个点状态往往与多个点的状态相互关联,我们要解决好多个状态之间的关系。
首先我们捋清楚 \(0/1\) 两个状态之间的转移关系。
由于对于一条边,我们必须选择一个节点,所以 \(0\) 不能转移到 \(0\),只能向 \(1\) 转移。而 \(1\) 就自由很多,可以转移到 \(0\),也可以继续保持 \(1\)。画出来就是这样:

下面我们分别看 \(f(u,0)\) 和 \(f(u,1)\) 怎么算。
对于 \(f(i,0)\),我们设它的子节点序列为 \(\{v_n\}\):
由上面的状态机得到:我们所有的子节点都应该是 \(1\) 状态。按照最后一个不同点,即子节点的不同划分一下集合:

综合 \(f\) 最小值的性质,我们得到:\(f(u,0)=\sum_{i=1}^nf(v_i,1)\)。
然后我们来看 \(f(u,1)\):
对于这个状态,子节点可以有 \(0/1\) 两种状态转移而来,我们按照这个可以将集合一分为二。

再结合状态的性质,得到 \(f(u,1)=(\sum_{i=1}^n\min\{f(v_i,0),f(v_i,1)\})\ +1\)。
总结一下,对于 \(u\) 点的状态,转移方程为:
接下来考虑边界情况。
当 \(u\) 为叶节点时,\(f(u,0)=0,f(u,1)=1\)。
#include <bits/stdc++.h>
using namespace std;
const int N=3000;
int n;
int f[N][2];
bool vis[N];
int head[N],ver[N],nxt[N],tot=0;
void add(int x,int y)
{
ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot;
}
void dfs(int x)
{
f[x][0]=0,f[x][1]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
dfs(y);
f[x][0]+=f[y][1];
f[x][1]+=min(f[y][0],f[y][1]);
}
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
memset(head,0,sizeof head),tot=0;
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++)
{
int x,k;
scanf("%d:(%d)",&x,&k);
for(int j=1;j<=k;j++)
{
int y;
scanf("%d",&y);
add(x,y);
vis[y]=1;
}
}
int root=0;
while(vis[root]) root++;
dfs(root);
printf("%d\n",min(f[root][0],f[root][1]));
}
return 0;
}
皇宫看守
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 \(n\),表示树中结点的数目。
第二行至第 \(n+1\) 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 \(i\),在该宫殿安置侍卫所需的经费 \(k\),该结点的子结点数 \(m\),接下来 \(m\) 个数,分别是这个结点的 \(m\) 个子结点的标号 \(r_1,r_2,…,r_m\)。
对于一个 \(n\) 个结点的树,结点标号在 \(1\) 到 \(n\) 之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
数据范围
\(1≤n≤1500\)
输入样例
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例
25
样例解释:
在\(2\)、\(3\)、\(4\)结点安排护卫,可以观察到全部宫殿,所需经费最少,为 \(16 + 5 + 4 = 25\)。
解析
我们考虑合法情况下,一个节点的状态。
合法情况下,一个节点的状态只有三个:被父节点看到,被子节点看到,它自己放一个哨兵。
考虑能否利用状态机模型的思想来设计 DP 。
- 设 \(f(x,k)\) 为在节点 \(x\) 的子树里面放哨兵,\(x\) 节点的状态为 \(k=0/1/2\) 的最小花费。
\(0,1,2\) 分别对应:被父节点看到,自己放一个,被子节点看到。
考虑三种状态之间的转移关系。
-
对于状态 \(0\) ,即被父节点看到:
由于我们 \(x\) 没有放哨兵,此时我们的子节点只是无法被父节点看到,\(1/2\) 两种状态均可。
设子节点为 \(u\),则
\[f(x,0)=\sum_v\min\{f(v,1),f(v,2)\} \] -
对于状态 \(1\) ,即自己放一个:
此时对于某个子节点,怎么放都是合法的。
所以
\[f(x,1)=w_x+\sum_v \min\{f(v,1),f(v,2),f(v,3)\} \] -
对于状态 \(2\),即被子节点看到:
首先我们要枚举 \(x\) 被哪个子节点看到了。假设这个子节点是 \(v^{\prime}\)。
那么除了 \(v^{\prime}\) 以外,其他的节点要么自己放要么被自己的子节点看到。
根据关系我们可以得出:
\[f(x,2)=\mathop{\text{Min}} _ {v^{\prime}}\{f(v^{\prime},1)+\sum_{v\ne v^{\prime}}\min\{\ f(v,1),f(v,2)\}\ \} \]我们发现 \(\sum_{v\ne v^{\prime}}\min\{\ f(v,1),f(v,2)\}\) 与 \(f(x,0)\) 的表达式很相似,将 \(f(x,0)\) 的表达式强行代入,得到:
\[f(x,2)=\mathop{\text{Min}} _{v^{\prime}}\{f(v^{\prime},1)+f(x,0)-\min\{f(v^{\prime},1),f(v^{\prime},2)\}\ \} \]
总结之:
考虑叶节点的边界情况。
叶节点可以被父节点看到,可以自己放一个,不能被子节点看到。
所以对于叶节点 \(u\),\(f(u,0)=0,f(u,1)=w_u,f(u,2)=+\infty\)。
#include <bits/stdc++.h>
using namespace std;
const int N=1510,INF=1e8;
int n;
int w[N],f[N][3],vis[N];
int head[N],ver[N],nxt[N],tot=0;
void add(int x,int y)
{
ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot;
}
void dfs(int x)
{
f[x][0]=0, f[x][1]=w[x];
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
dfs(y);
f[x][0]+=min(f[y][1],f[y][2]);
f[x][1]+=min(f[y][0],min(f[y][1],f[y][2]));
}
f[x][2]=INF;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
f[x][2]=min(f[x][2],f[y][1]+f[x][0]-min(f[y][1],f[y][2]));
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x,k;
scanf("%d",&x);
scanf("%d%d",&w[x],&k);
for(int i=1;i<=k;i++)
{
int y;
scanf("%d",&y);
add(x,y);
vis[y]++;
}
}
int root;
for(int i=1;i<=n;i++)
if(!vis[i]) root=i;
dfs(root);
printf("%d",min(f[root][1],f[root][2]));
return 0;
}
换根DP
树形DP的一个子类,解决无根树的 DP 问题。
某些 DP 要求的东西和 DP 开始的根有关系,比如要求以个节点为根统计一些东西。
解决这种问题一般使用二次扫描。
第一次扫描:以其中一个节点为根,求出其对应的 DP 值。
第二次扫描:根据节点与节点之间的关系,把当前的状态转移到换根后的状态。
概述总是抽象的,我们看一下实际应用
树的中心
给定一棵树,树中包含 \(n\) 个结点(编号 \(1~n\) )和 \(n−1\) 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 \(n\)。
接下来 \(n−1\) 行,每行包含三个整数 \(a_i\),\(b_i\),\(c_i\),表示点 \(a_i\) 和 \(b_i\) 之间存在一条权值为 \(c_i\) 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
\(1≤n≤10000, 1≤a_i,b_i≤n, 1≤c_i≤10^5\)
输入样例:
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例:
2
解析
我们很容易想到如何求解一个点到所有节点的最远距离。

我们先假设 \(1\) 号点作为根,最终求 \(1\) 号点到所有点的最远距离。
- 设 \(f(i)\) 表示 \(i\) 节点到其子树节点的最远距离。
显然,对于叶节点 \(x\) : \(f(x)=0\)
考虑非叶节点,寻找最后一个不同点,即根节点的子节点不同来划分集合:

这是一个具有最大属性的状态值,结合题目实际,得到状态转移方程:\(f(i)=\text{Max}_{fa(j)=i}\{f(j)+e _{i,j}\}\)。一遍 DFS 我们就可以求出当前根点的最大距离。
现在我们的问题是如何求出其他节点的最大距离。

我们来看看一棵树的某一部分。
对于 \(i\) 点,最长的距离路线有两种走法,一种是向下走,也就是往子树走,另外一种是往上走,也就是往父亲节点方向走。
向子树走的最大距离我们已经求出来了,问题集中于求 \(i\) 向上走的最大距离。
由我们第一个 DP 的过程推广,将 \(i\) 又看做 \(P\) 的父节点,我们可以得到 \(P\) 在这种情况下的子树内最大距离加上边权就是 \(i\) 的向上的最长距离。
现在我们要看一下 \(P\) “在那种情况下的子树中的最长路径”在当前这棵树中是什么样子:

从 \(i\) 点上来到 \(P\) 点,我们有两种选择:
-
继续向上走,也就是 \(P\) 向上走的最大距离。
-
向 \(P\) 的其他子树走,到 \(i\) 的兄弟的子树(如 \(i_2,i_3\) 等)当中去。也就是这个和 \(P\) 的最大距离有关,而 \(P\) 的最大路径又分两种情况:
-
最大路径不经过 \(i\) 点,那么我们可以顺利地取到 \(P\) 向子树走的最大距离。
-
最大路径经过 \(i\) 点,由于我们不能往回走走回 \(i\) 点,那么就只能取到次大值。
-
\(P\) 向上走的最大距离就是上面的几种方案取 \(\max\) 。同时,我们也意识到,在第一次 DP 的过程中我们还要记录次长距离,最长路经过的子节点。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n;
int head[N],ver[N<<1],nxt[N<<1],edg[N<<1],tot=0;
void add(int x,int y,int z)
{
ver[++tot]=y; edg[tot]=z; nxt[tot]=head[x];head[x]=tot;
}
int f[N],fr[N],g[N];//最长路,最长路对应的子节点,次长路
int dfs(int x,int fa)//一次扫描,求以 1 为根的 DP 值
{
g[x]=f[x]=0; fr[x]=x;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==fa) continue;
int dis=dfs(y,x)+edg[i];
if(dis>f[x])
{
g[x]=f[x];
f[x]=dis,fr[x]=y;
}
else if(dis>g[x]) g[x]=dis;
}
return f[x];
}
int h[N],ans=1e8;//向上走的最大距离
void dfs2(int x,int fa)//二次扫描,我们用父节点来更新子节点的信息
{
ans=min(ans,max(f[x],h[x]));
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==fa) continue;
h[y]=max(h[x],(fr[x]==y?g[x]:f[x]))+edg[i];// 向上走的最长路径
dfs2(y,x);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dfs(1,1);
dfs2(1,1);
printf("%d",ans);
}
基环树 DP
首先说说基环树是个什么玩意。
现在我们有一棵 \(n\) 个节点,\(n-1\) 条边的树。

我们往上随便加一条边,它就变成了一棵基环树:

从上面我们可以看出基环树的结构特点:一个环,环上的每个节点都可能挂着一棵树。
基环树同时也是一类特殊的仙人掌。
现在我们看一下相关的性质:
-
\(n\) 个点 \(n\) 条边的图不一定是基环树。\(n\) 点 \(n\) 边只是一个必要条件,还需保证联通等其他条件。
-
基环树有多种形态:
-
无向树:

\(n\) 点 \(n\) 边无向图
邻二异丙苯 -
外向树:

\(n\) 点 \(n\) 边有向图,且每个点都恰有一个入边。
-
内向树:

\(n\) 点 \(n\) 边有向图,且每个点都恰有一个出边。
-
-
我们将环为作为根,可以将上面的树分别处理,然后对环上的每棵树单独处理,最后处理环。
基环树最大的特点是什么?它有个环。
所以我们需要一个程序来找到这个环。
我一般用的是 DFS 。将 DFS 经过的路径用栈存起来,然后当我们的 DFS 搜到一个已经在路径中的点时,我们就搜到了环,只需要往这个重复点上回退即可以遍历这个环。
int fa[N],fw[N];//记录每一个节点的父亲,以及到父亲的权值
int cir[N],ed[N],cnt=0;//所有在环内的点,不同环的展开序列在 cir 中的终点,环的数量。
bool vis[N],ins[N];//是否搜到,是否在栈内(找环的时候用)
void dfs_c(int x,int from)//当前节点,来源边
{
vis[x]=ins[x]=1;
for(int i=head[x];~i;i=nxt[i])
{
if(i==(from^1)) continue;//防止返回父节点
int y=ver[i];
fa[y]=x; fw[y]=edg[i];
if(!vis[y]) dfs_c(y,i);
else if(ins[y])//找到了重复的点
{
++cnt;
ed[cnt]=ed[cnt-1];
for(int k=x;k!=y;k=fa[k])//往回跳
{
cir[++ed[cnt]]=k;
}
cir[++ed[cnt]]=y;//记得把这个重复点也加进去。
}
}
ins[x]=0;
}
找到环了之后,我们就可以将树和环分开处理了。
『IOI2008』Island
你准备游览一个公园,该公园由 \(N\) 个岛屿组成,当地管理部门从每个岛屿出发向另外一个岛屿建了一座桥,桥是可以双向行走的。
同时,每对岛屿之间都有一艘专用的往来两岛之间的渡船。
相对于乘船而言,你更喜欢步行。
你希望所经过的桥的总长度尽可能的长,但受到以下的限制:
可以自行挑选一个岛开始游览。
-
任何一个岛都不能游览一次以上。
-
无论任何时间你都可以由你现在所在的岛 \(S\) 去另一个你从未到过的岛 \(D\)。由 \(S\) 到 \(D\) 可以有以下方法:
- 步行:仅当两个岛之间有一座桥时才有可能。对于这种情况,桥的长度会累加到你步行的总距离中。
- 渡船:你可以选择这种方法,仅当没有任何桥和以前使用过的渡船的组合可以由 \(S\) 走到 \(D\)(当检查是否可到达时,你应该考虑所有的路径,包括经过你曾游览过的那些岛)。
注意,你不必游览所有的岛,也可能无法走完所有的桥。
请你编写一个程序,给定 \(N\) 座桥以及它们的长度,按照上述的规则,计算你可以走过的桥的最大长度。
输入格式
第 \(1\) 行包含整数 \(N\)。
第 \(2\dots N+1\) 行,每行包含两个整数 \(a\) 和 \(L\),第 \(i+1\) 行表示岛屿 \(i\) 上建了一座通向岛屿 \(a\) 的桥,桥的长度为 \(L\)。
输出格式
输出一个整数,表示结果。
对某些测试,答案可能无法放进 \(32\) 位整数。
数据范围
\(2≤N≤10^6, 1≤L≤10^8\)
输入样例:
7
3 8
7 2
4 2
1 4
1 9
3 4
2 3
输出样例:
24
解析
我们先来看一下这个图到底是个什么东西。
首先桥是双向的,这是一个无向图。
然后这是一个 \(n\) 点 \(n\) 边的无向图,我们可以合理怀疑这是一个基环树。
题目描述中也说了 “每个岛屿都向另一个岛屿建了一座桥。”,可以知道,这个图一定是一个基环树森林。
由于题目没保证联通,所以我们无法确定是否是一棵基环树。
那么现在我们就可以抽象题目问题了:
给定一个基环树森林,边带权。让我们求所有基环树的直径和。
基环树的直径:基环树中最长的简单路径。
我们考虑怎么求出一棵基环树的直径。
对最长路径上的两个点分情况讨论:
-
最长路径上的两个点在同一棵树中:
这个问题就是一个树形 DP 问题。\(O(n)\) 处理即可。
-
两个点不在同一棵树中:
我们看一下这是什么情况:

我们从树中的一个点出发,从树根进入环,然后在环上绕一个优弧,到达另一颗树中的某一个节点。
这又怎么求呢?
问题分成三部分,第一棵树从根向内走的最大距离,环上的距离,第二棵树从根向内走的最大距离。
首先我们可以预处理出来所有环上点向它的树内走的最大距离,设对于环上某个点 \(x\) ,向内走的最大距离为 \(d(x)\)。再设两个环上点 \(x,y\) 的最大距离是 \(dis(x,y)\),那么问题就是最大化 \(d(x)+dis(x,y)+d(y)\)。
我们想到暴力枚举环上的点对 \((a,b)\),但是环上的点数可以与 \(n\) 同阶,复杂度 \(O(n^2)\),这是不可接受的。所以我们要另想办法优化。
但首先我们还是看暴力枚举的伪代码:
for x ← 1 to n for y ← 1 to x-1我们只要这样就可以遍历到所有的点对。
假设我们的 \(1\sim n\) 是按照逆时针编号的,那么我们在遍历的时候相当于假设 \(y\) 在 \(x\) 的顺时针方向。
我们将其破环为链。
由于点与点之间的距离具有前缀的性质,所以我们可以记一个前缀和 \(S\),那么 \((x,y)\) 之间的距离就是 \(S_x-S_y\)。
我们要最大化的就是 \(d(x)+S_x+d(y)-S_y\)。
现在我们的 \(x\) 固定,我们要 \(O(1)\) 得到后面这个东西的最大值,没有修改。
很容易就想到单调队列了是吧?直接拿单调队列维护一下就好了。
总结一下我们要干的事情:
- 找到环,这个 \(O(n)\) dfs,用栈记录一下搜过的点即可。
- 对每棵树 \(O(n)\) 求到根的最大距离和直径。
- 在环上跑单调队列优化的 DP 。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e7+10,M=2e7+20;
int n;
int head[N],ver[M],nxt[M],edg[M],tot=0;
void add(int x,int y,int z)
{
ver[tot]=y; edg[tot]=z; nxt[tot]=head[x]; head[x]=tot++;
}
int fa[N],fw[N];//记录每一个节点的父亲,以及到父亲的权值
int cir[N],ed[N],cnt=0;//所有在环内的点,不同环的展开序列在 cir 中的终点,环的数量。
ll s[N],d[M],sum[M];//前缀和,破环为链后的dis,破环为链后的前缀和
bool vis[N],ins[N];//是否在栈内(dfs找环的时候用)
ll q[N],ans=0;//单个基环树的答案
void dfs_c(int x,int from)//当前节点,来源边
{
vis[x]=ins[x]=1;
for(int i=head[x];~i;i=nxt[i])
{
if(i==(from^1)) continue;
int y=ver[i];
fa[y]=x; fw[y]=edg[i];
if(!vis[y]) dfs_c(y,i);
else if(ins[y])//找到了重复的点
{
++cnt;
ed[cnt]=ed[cnt-1];
ll sum=edg[i];
for(int k=x;k!=y;k=fa[k])//往回跳,统计前缀和
{
s[k]=sum;
sum+=fw[k];
cir[++ed[cnt]]=k;
}
s[y]=sum,cir[++ed[cnt]]=y;//记得把这个重复点也加进去。
}
}
ins[x]=0;
}
ll dfs_d(int x,int f)
{
vis[x]=1;
ll d1=0,d2=0;
for(int i=head[x];~i;i=nxt[i])
{
int y=ver[i];
if(vis[y]||y==f) continue;
ll dis=dfs_d(y,x)+edg[i];
if(dis>d1) d2=d1,d1=dis;
else if(dis>d2) d2=dis;
}
ans=max(ans,d1+d2);//处理数的直径
return d1;//返回到根节点的最大距离
}
int main()
{
scanf("%d",&n);
memset(head,-1,sizeof head);
for(int i=1;i<=n;i++)
{
int a,L;
scanf("%d%d",&a,&L);
add(i,a,L); add(a,i,L);
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs_c(i,-1);//找到所有的环
memset(vis,0,sizeof vis);
for(int i=1;i<=ed[cnt];i++) vis[cir[i]]=1;
ll res=0;
for(int i=1;i<=cnt;i++)
{
ans=0;
int nn=0;//记录一下环的大小
for(int j=ed[i-1]+1;j<=ed[i];j++)
{
int k=cir[j];
d[nn]=dfs_d(k,k);//树形Dp搜直径
sum[nn]=s[k];//记录前缀和
++nn;
}
for(int j=0;j<nn;j++)//破环为链
d[nn+j]=d[j], sum[nn+j]=sum[j]+sum[nn-1];
int hh=0,tt=-1;//单调队列
for(int j=0;j<nn*2;j++)
{
while(hh<=tt && j-q[hh]>=nn) ++hh;
if(hh<=tt) ans=max(ans,d[j]+sum[j]+d[q[hh]]-sum[q[hh]]);
while(hh<=tt && d[q[tt]]-sum[q[tt]]<=d[j]-sum[j]) --tt;
q[++tt]=j;
}
res+=ans;
}
printf("%lld",res);
return 0;
}
『ZJOI2008』骑士
Z 国的骑士团是一个很有势力的组织,帮会中聚集了来自各地的精英。
他们劫富济贫,惩恶扬善,受到了社会各界的赞扬。
可是,最近发生了一件很可怕的事情:邪恶的 Y 国发起了一场针对 Z 国的侵略战争。
战火绵延五百里,在和平环境中安逸了数百年的 Z 国又怎能抵挡得住 Y 国的军队。
于是人们把所有希望都寄托在了骑士团身上,就像期待有一个真龙天子的降生,带领正义打败邪恶。
骑士团是肯定具备打败邪恶势力的能力的,但是骑士们互相之间往往有一些矛盾。
每个骑士有且仅有一个他自己最厌恶的骑士(当然不是他自己),他是绝对不会与最厌恶的人一同出征的。
战火绵延,生灵涂炭,组织骑士军团刻不容缓!
国王交给你了一个艰巨的任务:从所有骑士中选出一个骑士军团,使得军团内没有矛盾的两人,即不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况,并且使这支骑士军团最富有战斗力。
为描述战斗力,我们将骑士按照 \(1\) 至 \(N\) 编号,给每位骑士一个战斗力的估计,一个军团的战斗力为所有骑士的战斗力之和。
输入格式
输入第一行包含一个正整数 \(N\),描述骑士团的人数;
接下来 \(N\) 行每行两个正整数,按顺序描述每一名骑士的战斗力和他最痛恨的骑士。
输出格式
输出包含一行,一个整数,表示你所选出的骑士军团的战斗力。
数据范围
\(1\le N\le 10^6,\) 每名骑士的战斗力都是不大于 \(10^6\) 的正整数。
输入样例:
3
10 2
20 3
30 1
输出样例:
30
解析
\(n\) 个点, \(n\) 条边,每个点都一定有且只有一条出边。
这理应是一个基环树森林。
题目要求就是这个基环树森林的最大点权独立集。
我们首先考虑在树上怎么做。
很容易地想到 DP 。
-
状态设计:
设状态 \(f(x,k)\) 为在 \(x\) 点的子树里面选,\(x\) 点选或不选 ( \(k=0\) 或 \(1\) ) 能获得的最大总战斗力。
-
状态计算:
我们将树的一部分画出来考虑:

当我们 \(u\) 选择 \(1\) 状态时,所有的 \(v\) 不能选。所以 \(f(u,1)=w_u+\sum_vf(v,0)\)。
当我们的 \(u\) 选择 \(0\) 状态时,所有的 \(v\) 都爱选不选,对于每一个 \(v\) 我们都取最大值即可,即 \(f(u,0)=\sum_v max\{f(v,0),f(v,1)\}\)。
综上:\(\begin{cases}f(u,1)=w_u+\sum_vf(v,0)\\ f(u,0)=\sum_v max\{f(v,0),f(v,1)\}\end{cases}\)
在树上的问题其实就是 "没有上司的舞会" 一题。
那么我们来看环上问题怎么解决。
我们可以试图直接破环,对于环中的某一条边,我们考虑它两边点的取舍情况,然后就可以删去这条边了。删完这条边问题就是树上问题了。
具体的,我们画个图:

假设我们不选择 \(u\) ,那么 \((u,v)\) 这条边就没有意义,就可以直接删去了。所以我们只需要以这个点为根跑一遍正常的树形 DP 即可。
假设我们一定要选 \(u\),那么 \(v\) 必不能选,我们仍然将这条边断开,然后重新做一遍树形DP,但是我们要在 DP 的过程中将 \(v\) 特判掉。具体的,我们在做到 \(v\) 的时候,特殊判断其只有不选的情况即可。
同时我们可以发现,这样做断开任意一条环内边的贡献是一样的,所以对于一棵基环树我们随便断开一条即可。
对于这个基环树森林,我们单独算完每一棵基环树,答案相加即可。
时间复杂度 \(O(n)\)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10,M=2e6+10;
inline int read()
{
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9')
if(ch=='-') w=-1,ch=getchar();
else ch=getchar();
while(ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-48,ch=getchar();
return s*w;
}
int n;
int head[N],ver[M],nxt[M],tot=0;
bool rm[M];//标记被删掉的边
void add(int x,int y)
{
ver[tot]=y;
nxt[tot]=head[x];
head[x]=tot++;
}
int poi[N];
bool vis[N],ins[N];
ll f1[N][2],f2[N][2];//省一点清空的时间
ll ans=0;
void dfs_f(int x,int w,ll f[][2])
{
f[x][0]=0;
if(x!=w) f[x][1]=poi[x];
for(int i=head[x];~i;i=nxt[i])
{
if(rm[i]) continue;
int y=ver[i];
dfs_f(y,w,f);
f[x][0]+=max(f[y][0],f[y][1]);
if(x!=w) f[x][1]+=f[y][0];
}
}
void dfs_c(int x,int from)
{
vis[x]=ins[x]=1;
for(int i=head[x];~i;i=nxt[i])
{
int y=ver[i];
if(!vis[y]) dfs_c(y,i);
else if(ins[y])
{
rm[i]=1;//删边
dfs_f(y,-1,f1);
dfs_f(y,x,f2);
ans+=max(f1[y][0],f2[y][1]);
}
}
ins[x]=0;
}
int main()
{
n=read();
memset(head,-1,sizeof head);
for(int i=1;i<=n;i++)
{
poi[i]=read();
add(read(),i);
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs_c(i,-1);
printf("%lld",ans);
return 0;
}
创世纪
上帝手中有 \(N\) 种世界元素,每种元素可以限制另外 \(1\) 种元素,把第 \(i\) 种世界元素能够限制的那种世界元素记为 \(A[i]\)。
现在,上帝要把它们中的一部分投放到一个新的空间中去建造世界。
为了世界的和平与安宁,上帝希望所有被投放的世界元素都有至少一个没有被投放的世界元素限制它。
上帝希望知道,在此前提下,他最多可以投放多少种世界元素?
输入格式
第一行是一个整数 \(N\),表示世界元素的数目。
第二行有 \(N\) 个整数 \(A_1,A_2,…,A_N\)。\(A_i\) 表示第 \(i\) 个世界元素能够限制的世界元素的编号。
输出格式
一个整数,表示最多可以投放的世界元素的数目。
数据范围
\(1\le N\le 10^6,1≤A_i≤N\)
输入样例:
6
2 3 1 3 6 5
输出样例:
3
解析
\(n\) 点 \(n\) 边有向图,每个点有且仅有一条出边。
我们可以1轻易地猜出这是一个基环树森林。
抽象一下问题,给定一个基环树森林,选出一个点集使得对于图中任意一条边,总存在一个端点不在点集之中,求点集的最大元素数。
仍然先考虑树上怎么做。
- 设 \(f(u,0/1)\) 为在第 \(u\) 个点的子树中选,第 \(u\) 个点选或( \(0\)) 者不选( \(1\) )的最大价值。
将树的一部分画出来分析。

假设我们不选 \(u\) 点,那么它的子节点可以随便选。
也就是 \(f(u,0)=\sum_v \max\{f(v,0),f(v,1)\}\)
假设我们选了 \(u\) ,那么其子节点内有一个必不选,其他的点随意。我们只需枚举这个点即可。
也就是 \(f(u,1)=\mathop{\text{Max}}_v\{f(v,0)+f(u,0)-\max\{f(v,1),f(v,0)\}+1\}\)
那么树上的问题解决完了,我们如何解决环上的?
仍然考虑直接枚举某一条边上的端点的状态,然后暴力破开这个环。

考虑图中的情况。
我们删去 \((u,v)\) 这条边,那么如果我们不选 \(v\),则 \(u\) 爱选不选;如果我们选了 \(v\) 那么 \(u\) 一定会选。
还是做两遍树形 DP ,特判 \(v\) 点即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e7+10,M=2e7+10,INF=1e9;
int read()
{
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9')
if(ch=='-') w=-1,ch=getchar();
else ch=getchar();
while(ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-'0',ch=getchar();
return s*w;
}
int n;
int head[N],ver[M],nxt[M],tot=0;
void add(int x,int y)
{
ver[tot]=y; nxt[tot]=head[x]; head[x]=tot++;
}
bool rm[M];
bool vis[N],ins[N];
int f1[N][2],f2[N][2];
int res=0;
void dfs_f(int x,int ww,int f[][2])
{
f[x][0]=0;
for(int i=head[x];~i;i=nxt[i])
{
if(rm[i]) continue;
int y=ver[i];
dfs_f(y,ww,f);
f[x][0]+=max(f[y][0],f[y][1]);
}
f[x][1]=-INF;
for(int i=head[x];~i;i=nxt[i])
{
int y=ver[i];
if(!rm[i])
f[x][1]=max(f[x][1],f[x][0]-max(f[y][0],f[y][1])+f[y][0]+1);
}
if(x==ww) f[x][1]=f[x][0]+1,f[x][0]=-INF;
}
void dfs_c(int x)
{
vis[x]=ins[x]=1;
for(int i=head[x];~i;i=nxt[i])
{
int y=ver[i];
if(!vis[y]) dfs_c(y);
else if(ins[y])
{
rm[i]=1;
dfs_f(y,-1,f1);
dfs_f(y,x,f2);
res+=max(max(f1[y][0],f1[y][1]),f2[y][0]);
}
}
ins[x]=0;
}
int main()
{
memset(head,-1,sizeof head);
scanf("%d",&n);
for(int i=1;i<=n;i++) add(read(),i);
for(int i=1;i<=n;i++)
if(!vis[i]) dfs_c(i);
printf("%d",res);
return 0;
}
(暂时就三个例题吧/kk)

