动态规划中的各种模型 <一>
本文对 DP 的分析方法基于以下文章中的内容:
主要针对各类Dp模型及例题做法,更偏向讲解题目与模板之间的转化与扩展。
当然,也不一定全是DP(Dp不可做的题使用“*”标记),更重要的是关注题目模型。
为了尽量节省篇幅(太长会卡),部分较为简单的题代码压了行,有需要可以将其复制到编辑器然后格式化。
数字三角形模型
模型最初来源于 [IOI1994]数字三角形
摘花生
Hello Kitty想摘点花生送给她喜欢的米老鼠。
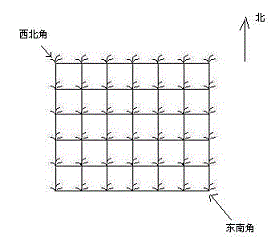
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数 \(T\) ,代表一共有多少组数据。
接下来是 \(T\) 组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数 \(R\) 和列数 \(C\)。
每组数据的接下来 \(R\) 行数据,从北向南依次描述每行花生苗的情况。每行数据有 \(C\) 个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目 \(M\)。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
\(1≤T≤100,\\ 1≤R,C≤100,\\ 0≤M≤1000\)
输入样例:
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例:
8
16
解析
这是一个非常常规的数字三角形模型。
观察得知,每个位置只能由左边和上面转移而来。
我们定义状态 \(f[i][j]\) 为从起点走到第 \(i\) 行第 \(j\) 列时的所有方案中能得到的最大花生数目。
这个状态只能左边或者上面的所有方案集合中转移过来。
转移方式也是直接转移,即 \(f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j]\)。
就是这样。
#include <bits/stdc++.h>
using namespace std;
int n;
const int N=110;
int w[N][N];
int f[N][N];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) scanf("%d",&w[i][j]);
}
memset(f,0,sizeof f);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j];
}
printf("%d\n",f[n][m]);
}
return 0;
}
对于 DP 状态计算时对状态的划分,有一个很重要的依据或者说是思考方向:“最后”。
在这个题里面,我们是依据最后一步怎么走来划分各类状态。最后一步的走法只有两种情况:向右走到当前位置或向下走到当前位置。即:

而划分的出来的集合要求不重不漏,尤其是对于求和类的状态来说。
当然,我们并不是绝对不能违反,最重要的是 对答案没有影响。
最低通行费
一个商人穿过一个 \(N×N\) 的正方形的网格,去参加一个非常重要的商务活动。
他要从网格的左上角进,右下角出。
每穿越中间 \(1\) 个小方格,都要花费 \(1\) 个单位时间。
商人必须在 \((2N-1)\) 个单位时间穿越出去。
而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。
请问至少需要多少费用?
注意:不能对角穿越各个小方格(即,只能向上下左右四个方向移动且不能离开网格)。
输入格式
第一行是一个整数,表示正方形的宽度N。
后面 \(N\) 行,每行 \(N\) 个不大于 \(100\) 的整数,为网格上每个小方格的费用。
输出格式
输出一个整数,表示至少需要的费用。
数据范围
\(1≤N≤100\)
输入样例:
5
1 4 6 8 10
2 5 7 15 17
6 8 9 18 20
10 11 12 19 21
20 23 25 29 33
输出样例:
109
样例解释
样例中,最小值为 \(109=1+2+5+7+9+12+19+21+33\) 。
解析
看完题面,对于 \(2n-1\) 这个步数限制,我们可以知道从左上到右下的曼哈顿距离刚好是 \(2n-1\) 所以我们只能向右或向下走。
那么这个题就和上面一模一样,只是求最小值罢了。
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,f[N][N],w[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&w[i][j]);
memset(f,0x3f,sizeof f);
f[1][0]=0,f[0][1]=0;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) f[i][j]=min(f[i-1][j],f[i][j-1])+w[i][j];
printf("%d",f[n][n]);
return 0;
}
方格取数
设有 \(N×N\) 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
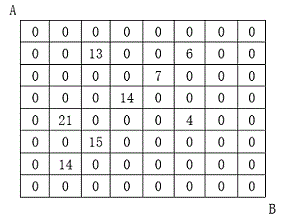
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
输入格式
第一行为一个整数 \(N\),表示 \(N×N\) 的方格图。
接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。
行和列编号从 \(1\) 开始。
一行“\(0 0 0\)”表示结束。
输出格式
输出一个整数,表示两条路径上取得的最大的和。
数据范围
\(N≤10\)
输入样例
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例
67
解析
我们想想如何表示状态表示:
在上面的题中,我们只走一次,但是在这个图中,我们要走两次。
我们可以试着让他们同时出发。
设 \(f[i_1][j_1][i_2][j_2]\),为两条道路分别从 \((1,1)\) 走到 \((i_1,j_1),(i_2,j_2)\) 的所有方案中的最大值。
由上面的题我们知道,一条道路有两种情况,两条道路的情况便是它们自由组合得到的数字。
也就是说,\(f[i][j][k][l]=max(f[i-1][j][k-1][l],f[i][j-1][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k][l-1])+w[i][j]+w[k][l]\)
现在考虑题中的另一个限制条件:每个格子中的数只能被取一次。也就是说,当 \((i,j)=(k,l)\) 时,我们只加一次 \(w\) 即可。
然后是对状态的优化。
这两条路线有一个很大的共同点:它们的步数应当相同。
也就是说 \(i+j=k+l\) 应当成立。
据此,我们可以优化掉一维的状态:令 \(S=i+j=k+l\) 那么我们可以用 \(f[S][i][j]\) 表示:从 \((1,1)\) 开始分别走到 \((i,S-i),(j,S-j)\) 的所有方案中取得的最大值,\(S\in [1,2n]\)。
#include <bits/stdc++.h>
using namespace std;
const int N=100;
int f[N][N][N];
int w[N][N];
int main()
{
int n,x,y,z;
scanf("%d",&n); while(scanf("%d%d%d",&x,&y,&z)!=EOF&&x&&y&&z) w[x][y]=z;
for(int k=1;k<=2*n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
f[k][i][j]=max(max(f[k-1][i][j-1],f[k-1][i-1][j]),max(f[k-1][i-1][j-1],f[k-1][i][j]))+w[i][k-i];
if(i!=j) f[k][i][j]+=w[j][k-j];
}
printf("%d",f[2*n][n][n]);
return 0;
}
传纸条
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 \(m\) 行 \(n\) 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 \((1,1)\),小轩坐在矩阵的右下角,坐标 \((m,n)\)。
从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 \(0\) 表示),可以用一个 \(0\sim 100\) 的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有 \(2\) 个用空格隔开的整数 \(m\) 和 \(n\),表示学生矩阵有 \(m\) 行 \(n\) 列。
接下来的 \(m\) 行是一个 \(m×n\) 的矩阵,矩阵中第 \(i\) 行 \(j\) 列的整数表示坐在第 \(i\) 行 \(j\) 列的学生的好心程度,每行的 \(n\) 个整数之间用空格隔开。
输出格式
输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
\(1≤n,m≤50\)
输入样例:
3 3
0 3 9
2 8 5
5 7 0
输出样例:
34
解析
和上一题仍然相似,还是选两条路线。
我们设计状态:\(f[i_1][j_1][i_2][j_2]\) 表示两条路线从各自的起点到达 \((i_1,j_1),(i_2,j_2)\) 的所有方案。
仍然只能向右向下走,所以我们的状态转移与上面一致。
但是多了一条路径不能重复的限制,我们在枚举 \(i,j\) 时注意判断。
当然,我们仍然可以使用上一题的压维优化。
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int f[N][N][N],w[N][N];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%d",&w[i][j]);
for(int k=1;k<=m+n;k++)
for(int i=max(1,k-m);i<=min(n,k-1);i++)
for(int j=max(1,k-m);j<=min(n,k-1);j++)
{
f[k][i][j]=max(max(f[k-1][i-1][j],f[k-1][i-1][j-1]),max(f[k-1][i][j],f[k-1][i][j-1]))+w[i][k-i];
if(i!=j) f[k][i][j]+=w[j][k-j];
}
printf("%d",f[n+m][n][n]);
return 0;
}
K取方格数*
在一个\(N\times N\) 的矩形网格中,每个格子里都写着一个非负整数。
可以从左上角到右下角安排 \(K\) 条路线,每一步只能往下或往右,沿途经过的格子中的整数会被取走。
若多条路线重复经过一个格子,只取一次。
求能取得的整数的和最大是多少。
输入格式
第一行包含两个整数 \(N\) 和 \(K\)。
接下来 \(N\) 行,每行包含 \(N\) 个不超过 \(1000\) 的整数,用来描述整个矩形网格。
输出格式
输出一个整数,表示能取得的最大和。
数据范围
\(1≤N≤50, 0≤K≤10\)
输入样例:
3 2
1 2 3
0 2 1
1 4 2
输出样例:
15
解析
数字三角形的终极版。
这一次它的路径条数不固定了,我们不敢确定要开多少维数组(20维也开不下),要另想办法。
将每个格子看做点,向右边和下边连单向边,我们发现这个题被转化成了在一个有向图中最大化一个什么东西。由于多条路径,最短路不大可做,我们考虑网络流。
每条边能够随便通过,所以我们将边的容量设为正无穷。由于每个点还有使用限制,我们套路地拆点。首先连一条容量为 \(1\) 的边,表示这个点只能被取一次权值,权值我们自然使用费用来表达;再连一条容量为 \(+\infty\) 的边,表示这个点能够无限次通过。
最后我们如何限制路径条数?
建立源点、汇点,源点连向左上角,右下角连向汇点,容量为 \(k\)。
之后只需要EK求最大费用流即可。
code:
#include <bits/stdc++.h>
using namespace std;
const int N=2e4+10, M=4e5+10, INF=1e8+10;
int n,k,S,T;
int head[N],ver[M],nxt[M],cc[M],ww[M],tot=0;
void add(int x,int y,int c,int d)
{
ver[tot]=y; cc[tot]=c; ww[tot]=d; nxt[tot]=head[x]; head[x]=tot++;
ver[tot]=x; cc[tot]=0; ww[tot]=-d; nxt[tot]=head[y]; head[y]=tot++;
}
int q[N],d[N],pre[N],incf[N];
bool vis[N];
inline int get(int x,int y) {return (x-1)*n+y;}
bool spfa()
{
int hh=0,tt=1;
memset(d,-0x3f,sizeof d);
memset(incf,0,sizeof incf);
q[0]=S; d[S]=0,incf[S]=INF;
while(hh!=tt)
{
int x=q[hh++];
if(hh==N) hh=0;
vis[x]=0;
for(int i=head[x];~i;i=nxt[i])
{
int y=ver[i];
if(cc[i] && d[y]<d[x]+ww[i])
{
d[y]=d[x]+ww[i];
pre[y]=i;
incf[y]=min(cc[i],incf[x]);
if(!vis[y])
{
q[tt++]=y;
if(tt==N) tt=0;
vis[y]=1;
}
}
}
}
return incf[T]>0;
}
int EK()
{
int cost=0;
while(spfa())
{
int tmp=incf[T];
cost+=tmp*d[T];
for(int i=T;i!=S;i=ver[pre[i]^1])
{
cc[pre[i]]-=tmp;
cc[pre[i]^1]+=tmp;
}
}
return cost;
}
int main()
{
scanf("%d%d",&n,&k);
memset(head,-1,sizeof head);
S=0,T=n*n*2+100; int B=n*n+5;
add(S,1,k,0);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
int x; scanf("%d",&x);
int pos=get(i,j);
add(pos,B+pos,1,x); add(pos,B+pos,INF,0);
if(i+1<=n) add(B+pos,get(i+1,j),INF,0);
if(j+1<=n) add(B+pos,get(i,j+1),INF,0);
}
}
add(B+get(n,n),T,k,0);
printf("%d",EK());
return 0;
}
最长子序列模型
LIS 问题:
给定一个长度为 \(n\) 的序列 \(\{a_n\}\),求其最长上升子序列的长度。
\(n\le 1000,a_i\in[-10^9,10^9]\)。
这个问题是一个经典的Dp问题。
这是一个一维问题,一般状态只需要一维。
设状态 \(f[i]\) ,它的属性一定是数量。考虑这个状态所表示的方案集合,我们可以设 \(f[i]\) 是以 \(a_i\) 为结尾的所有上升子序列方案中能得到的最长长度,下面我们分析它所表示集合的组成。
我们按照这个序列的倒数第二个数来分类:

那么我们假设 \(a_k\) 是倒数第二位数字,看看如何计算状态。
此时 \(a_k\) 有 \(i-1\) 个不同情况,我们一一枚举即可。
也就是说,\(f[i]=max\{f[k]\}+1,\ k\in [1,i) \land a_k<a_i\)。
这个题是所有这类问题的基础。
怪盗基德的滑翔翼
怪盗基德是一个充满传奇色彩的怪盗,专门以珠宝为目标的超级盗窃犯。
而他最为突出的地方,就是他每次都能逃脱中村警部的重重围堵,而这也很大程度上是多亏了他随身携带的便于操作的滑翔翼。
有一天,怪盗基德像往常一样偷走了一颗珍贵的钻石,不料却被柯南小朋友识破了伪装,而他的滑翔翼的动力装置也被柯南踢出的足球破坏了。
不得已,怪盗基德只能操作受损的滑翔翼逃脱。
城市中一共有N幢建筑排成一条线,每幢建筑的高度各不相同。
初始时,怪盗基德可以在任何一幢建筑的顶端。
他可以选择一个方向逃跑,但是不能中途改变方向(因为中森警部会在后面追击)。
因为滑翔翼动力装置受损,他只能往下滑行(即:只能从较高的建筑滑翔到较低的建筑)。
他希望尽可能多地经过不同建筑的顶部,这样可以减缓下降时的冲击力,减少受伤的可能性。
请问,他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)?
输入格式
输入数据第一行是一个整数 \(K\),代表有 \(K\) 组测试数据。
每组测试数据包含两行:第一行是一个整数 \(N\),代表有 \(N\) 幢建筑。第二行包含 \(N\) 个不同的整数,每一个对应一幢建筑的高度 \(h\) ,按照建筑的排列顺序给出。
输出格式
对于每一组测试数据,输出一行,包含一个整数,代表怪盗基德最多可以经过的建筑数量。
数据范围
\(1≤K≤100,\\ 1≤N≤100,\\ 0<h<10000\)
输入样例:
3
8
300 207 155 299 298 170 158 65
8
65 158 170 298 299 155 207 300
10
2 1 3 4 5 6 7 8 9 10
输出样例:
6
6
9
解析
这是一个线性问题,所以基德的方向只有两种。
我们定义从左到右(即按给出的顺序)为正向,从右到左为反向。
那么本题就是让我们求两个方向上的最长严格下降子序列。
而正向的最长下降就是反向的最长上升,所以这个题是在让我们求两个方向上的最长上升子序列。
\(O(2n^2)\) 直接解决即可。
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int w[N],f[N];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n; scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]),f[i]=1;
for(int i=1;i<=n;i++) for(int j=1;j<i;j++)
if(w[j]<w[i]) f[i]=max(f[i],f[j]+1);
int max1=0;
for(int i=1;i<=n;i++) max1=max(max1,f[i]),f[i]=1;
for(int i=n;i>=1;i--) for(int j=n;j>i;j--)
if(w[j]<w[i]) f[i]=max(f[i],f[j]+1);
for(int i=1;i<=n;i++) max1=max(max1,f[i]);
printf("%d\n",max1);
}
return 0;
}
登山
五一到了,ACM队组织大家去登山观光,队员们发现山上一个有N个景点,并且决定按照顺序来浏览这些景点,即每次所浏览景点的编号都要大于前一个浏览景点的编号。
同时队员们还有另一个登山习惯,就是不连续浏览海拔相同的两个景点,并且一旦开始下山,就不再向上走了。
队员们希望在满足上面条件的同时,尽可能多的浏览景点,你能帮他们找出最多可能浏览的景点数么?
输入格式
第一行包含整数 \(N\),表示景点数量。
第二行包含 \(N\) 个整数,表示每个景点的海拔。
输出格式
输出一个整数,表示最多能浏览的景点数。
数据范围
\(2≤N≤1000\)
输入样例:
8
186 186 150 200 160 130 197 220
输出样例:
4
解析
读题,抽取得到以下信息
- 访问景点海拔序列要么单调递增,要么单调递增后单调递减。
- 最大化序列长度
我们有了上一题的经验,将这个序列拆开,分别处理以分界点为终点的最长上升子序列和以这个点为起点的最长下降子序列,以一个点为起点的最长严格下降子序列就是反向情况下以这个点为终点的最长严格上升子序列。最后统计答案,打擂台取最大值。
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int w[N],f1[N],f2[N];
int main()
{
int n; scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]),f1[i]=f2[i]=1;
for(int i=1;i<=n;i++) for(int j=1;j<i;j++)
if(w[i]>w[j]) f1[i]=max(f1[i],f1[j]+1);
for(int i=n;i>0;i--) for(int j=n;j>i;j--)
if(w[i]>w[j]) f2[i]=max(f2[i],f2[j]+1);
int res=0;
for(int i=1;i<=n;i++) res=max(res,f1[i]+f2[i]-1);
printf("%d",res);
return 0;
}
友好城市
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。
北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。
编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
输入格式
第 \(1\) 行,一个整数 \(N\) ,表示城市数。
第 \(2\) 行到第 \(n+1\) 行,每行两个整数,中间用 \(1\) 个空格隔开,分别表示南岸和北岸的一对友好城市的坐标。
输出格式
仅一行,输出一个整数,表示政府所能批准的最多申请数。
数据范围
\(1≤N≤5000, 0≤xi≤10000\)
输入样例:
7
22 4
2 6
10 3
15 12
9 8
17 17
4 2
输出样例:
4
解析
观察题目,整理信息:
- 一条数轴上的给定点向另外一个平行数轴上的给定点连边。
- 一个点只有一个对应的点
- 连边之间不能有交叉
- 求最长能连边的点对数目
我们画出某种合法方案的示意图。

以上方的轴为 \(A\) 轴,另一根为 \(B\) 轴,那么将 \(A\) 轴上的点的顺序作为基准, \(B\) 轴上对应的点的坐标是单调递增的。
也就是说,我们将友好城市对按照其中一边的城市坐标排序,最大批准数方案就是另外一根轴上恒坐标的最长上升子序列长度。
#include <bits/stdc++.h>
using namespace std;
const int N=5010;
struct node{int x,y;} poi[N];
bool cmp(node a,node b) {return a.x<b.x;}
int f[N];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int a,b;
scanf("%d%d",&a,&b);
poi[i]={a,b}; f[i]=1;
}
sort(poi+1,poi+1+n,cmp);
for(int i=1;i<=n;i++) for(int j=1;j<i;j++)
if(poi[j].y<poi[i].y) f[i]=max(f[i],f[j]+1);
int ans=1;
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
printf("%d",ans);
return 0;
}
拦截导弹
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。
但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
某天,雷达捕捉到敌国的导弹来袭。
由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于 \(30000\) 的正整数,导弹数不超过 \(1000\) ),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式
共一行,输入导弹依次飞来的高度。
输出格式
第一行包含一个整数,表示最多能拦截的导弹数。
第二行包含一个整数,表示要拦截所有导弹最少要配备的系统数。
数据范围
雷达给出的高度数据是不大于 \(30000\) 的正整数,导弹数不超过 \(1000\)。
输入样例:
389 207 155 300 299 170 158 65
输出样例:
6
2
解析
本题分为两个小问:
- 序列的最长下降子序列长度
- 最少几个下降子序列能够覆盖全序列。
第一问只需要 套模板 即可。
现在我们的问题是第二问。
从贪心的角度想,对于一个数,我们有两种选择:
- 重新开一个下降子序列,将其单独放入
- 在已有且能放置的序列后面将这个数添上
我们要使得存在的下降子序列数最小,那么我们就要尽量不新建序列。
而且,我们还要将它接到结尾大于它且最小的子序列上。
贪心策略如下:
- 当前存在序列结尾所有的数都小于当前数时,我们新建一个序列。
- 将当前的数放到结尾大于它且最接近它的子序列后面
知道了策略,想想怎么实现。
我们开一个数组 \(g\) 存放已建立的所有子序列的结尾数字,假设它现在是有序的(这很容易做到)。
现在我们要插入一个数 \(x\) ,我们首先要在 \(g\) 中找到大于 \(x\) 的最小数,然后将其替换掉,由于被替换的位置前的数小于 \(x\),位置后的数大于 \(x\) ,我们下一个数继续二分即可。
另外一种思路:Dilworth 定理
我们直接用 Dilworth 定理推:将一个导弹描述为一个二元组 \((a,b)\) ,\(a\) 是导弹的到达顺序, \(b\) 为导弹高度。设二元组偏序关系 \((a_1,b_1)\le(a_2,b_2)\) 为 \(a_1<a_2\land b_1 \le b_2\),问题就是在求最少能够划分多少个全序集能将所有元素覆盖。根据 Dilworth 定理,我们只需求最大反链元素个数即可,即求最大严格上升子序列元素个数。使用最大上升子序列的贪心解法代码则与上文相同。
还有一种思路:建图
我们还可以直接从大数向小数连边得到一个DAG然后做最小路径覆盖问题,可以使用匈牙利/网络流解决。
code:(求最长上升子序列使用贪心解法)
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n=1;
int a[N],g[N];
int main()
{
while(scanf("%d",&a[n])!=EOF) ++n; --n;
int tot=1; g[tot]=a[1];
for(int i=2;i<=n;i++)
{
if(a[i]<=g[tot]) g[++tot]=a[i];//新建
else {
int l=upper_bound(g+1,g+1+tot,a[i],greater<int>())-g;//greater后面不加括号会过不了编译?
g[l]=a[i];
}
}
printf("%d\n",tot);
tot=1; g[tot]=a[1];
for(int i=2;i<=n;i++)
{
if(a[i]>g[tot]) g[++tot]=a[i];
else{
int l=lower_bound(g+1,g+1+tot,a[i])-g;
g[l]=a[i];
}
}
printf("%d",tot);
return 0;
}
导弹拦截系统
3s/64M
又是导弹
为了对抗附近恶意国家的威胁,R 国更新了他们的导弹防御系统。
一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。
例如,一套系统先后拦截了高度为 \(3\) 和高度为 \(4\) 的两发导弹,那么接下来该系统就只能拦截高度大于 \(4\) 的导弹。
给定即将袭来的一系列导弹的高度,请你求出至少需要多少套防御系统,就可以将它们全部击落。
输入格式
输入包含多组测试用例。
对于每个测试用例,第一行包含整数 \(n\),表示来袭导弹数量。
第二行包含 \(n\) 个不同的整数,表示每个导弹的高度。
当输入测试用例 \(n=0\) 时,表示输入终止,且该用例无需处理。
输出格式
对于每个测试用例,输出一个占据一行的整数,表示所需的防御系统数量。
数据范围
\(1≤n≤50\)
输入样例:
5
3 5 2 4 1
0
输出样例:
2
样例解释
对于给出样例,最少需要两套防御系统。
一套击落高度为 \(3,4\) 的导弹,另一套击落高度为 \(5,2,1\) 的导弹。
解析
我们没有一个好的办法去判定一个导弹应该被上升子序列选中还是被下降子序列选中,所以我们直接爆搜,然后套上面的做法。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n;
int poi[N];
int up[N],down[N];
int ans=1145141919;
void dfs(int u,int l1,int l2)
{
if(l1+l2>=ans) return ;//最优化剪枝
if(u==n) {ans=l1+l2; return ;}
int tmp;
/*将其放入上升序列中*/
if(poi[u]>up[l1]) tmp=up[l1+1],up[l1+1]=poi[u],dfs(u+1,l1+1,l2),up[l1+1]=tmp;
else{
int l=lower_bound(up+1,up+1+l1,poi[u])-up;
tmp=up[l]; up[l]=poi[u]; dfs(u+1,l1,l2);
up[l]=tmp;
}
/*将其放入下降序列中*/
if(poi[u]<down[l2]) tmp=down[l2+1],down[l2+1]=poi[u],dfs(u+1,l1,l2+1),down[l2+1]=tmp;
else{
int l=lower_bound(down+1,down+1+l2,poi[u],greater<int>())-down;
tmp=down[l]; down[l]=poi[u]; dfs(u+1,l1,l2);
down[l]=tmp;
}
}
int main()
{
while(scanf("%d",&n)!=EOF&&n)
{
for(int i=1;i<=n;i++)
scanf("%d",&poi[i]);
ans=n;
memset(down,0x3f,sizeof down);
dfs(1,0,0);
printf("%d\n",ans);
}
return 0;
}
最长公共上升子序列
熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。
小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共子序列,现在又让他们研究最长公共上升子序列了。
小沐沐说,对于两个数列 \(A\) 和 \(B\),如果它们都包含一段位置不一定连续的数,且数值是严格递增的,那么称这一段数是两个数列的公共上升子序列,而所有的公共上升子序列中最长的就是最长公共上升子序列了。
奶牛半懂不懂,小沐沐要你来告诉奶牛什么是最长公共上升子序列。
不过,只要告诉奶牛它的长度就可以了。
数列 \(A\) 和 \(B\) 的长度均不超过 \(3000\)。
输入格式
第一行包含一个整数 \(N\),表示数列 \(A,B\) 的长度。
第二行包含 \(N\) 个整数,表示数列 \(A\)。
第三行包含 \(N\) 个整数,表示数列 \(B\)。
输出格式
输出一个整数,表示最长公共上升子序列的长度。
数据范围
\(1≤N≤3000\),序列中的数字均不超过 \(2^{31}−1\)。
输入样例:
4
2 2 1 3
2 1 2 3
输出样例:
2
解析
LIS 与 LCS 的结合。
我们重新设计状态
设 \(f(i,j)\) 表示 由第一个序列前 \(i\) 个元素和第二个序列前 \(j\) 个元素组成的且以 \(b[j]\) 结尾的最长公共上升子序列,所能得到的长度最大值。
现在我们考虑状态的计算:
参照公共子序列的集合划分的方式,由于状态定义中我们已经使 \(b[j]\) 一定在序列中,所以我们只需要讨论 \(a[i]\) 的情况。

右边的子集就是 \(f(i-1,j)\) ,剩下的问题就是左边的集合。
首先我们要明确的是,只有当 \(a_i=b_j\) 时才有左集合。
我们将这个集合继续分解,由于 \(b[j]\) 已经确定,我们可以按照倒数第二个位置的数分为 \(j-1\) 类。

对于每一个代表 \(b_k\) 的小集合,我们都可以表示为 \(f(i,k)\) 。也就是说,只考虑左集合的状态转移是 \(f(i,j)=max\{f(i,k)+1\}\)
先给暴力code:
#include <bits/stdc++.h>
using namespace std;
const int N=3010;
int n;
int a[N],b[N];
int f[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
f[i][j]=f[i-1][j];
if(a[i]==b[j])
{
f[i][j]=max(f[i][j],1);//特判空集
for(int k=1;k<j;k++)
if(b[k]<b[j]) f[i][j]=max(f[i][j],f[i-1][k]+1);
}
}
}
int res=0;
for(int i=1;i<=n;i++) res=max(f[n][i],res);
printf("%d",res);
return 0;
}
这个暴力很好卡,只需要两个序列完全一样就能卡成 \(n^3\) 。
下面我们开始优化。
Dp优化最基本的方式是对代码进行恒等变形。
由于 \(a[i]=b[j]\) 所以 if(b[k]<b[j]) 变为 if(b[k]<a[i]) 。也就是我们要求的是:在满足一个与 \(j\) 毫无关系的条件的情况下,\(f[i][j]\) 的一个最大前缀。
我们可以使用一个变量来存储这个值,然后边做边维护这个值。
code
#include <bits/stdc++.h>
using namespace std;
const int N=3010;
int n;
int a[N],b[N];
int f[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
{
int maxv=1;//f[i][j]的最大前缀
for(int j=1;j<=n;j++)
{
f[i][j]=f[i-1][j];
if(a[i]==b[j]) f[i][j]=max(f[i][j],maxv);
if(b[j]<a[i]) maxv=max(maxv,f[i][j]+1);
}
}
int res=0;
for(int i=1;i<=n;i++) res=max(f[n][i],res);
printf("%d",res);
return 0;
}
状态机模型
当然,我们只会用到一些简单的概念。
比如说我们玩游戏,某角色有站立,跑,攻击等状态
站立状态通过某种转换方式可以直接转换到跑步状态,跑步状态也可以通过某种方式转换到站立状态,而站立和跑步都可以转换到攻击状态,同样,攻击状态也可以转换回去。

大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 \(N\) 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 \(T\),表示一共有 \(T\) 组数据。
接下来的每组数据,第一行是一个整数 \(N\) ,表示一共有 \(N\) 家店铺。
第二行是 \(N\) 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过 \(1000\) 。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
\(1≤T≤50, 1≤N≤10^5\)
输入样例:
2
3
1 8 2
4
10 7 6 14
输出样例:
8
24
样例解释
对于第一组样例,阿福选择第 \(2\) 家店铺行窃,获得的现金数量为 \(8\)。
对于第二组样例,阿福选择第 \(1\) 和 \(4\) 家店铺行窃,获得的现金数量为 \(10+14=24\)。
解析
一般做法:
设 \(f(i)\) 表示抢前 \(i\) 家店铺获得的最大现金。
考虑最后一步,将集合分为两部分

得到状态转移方程: \(f[i]=max(f[i-2]+w[i],f[i-1])\)。
实际上,这个方法已经可做了。
但是我们使用这种方法并不能找到这个店铺是否被选中了,所以我们将状态分为两部分,即再开一维表示这个店铺是否被选。
我们集中分析这个 \(01\) 状态之间的关系。
假设当前我们不选这个商店,那么下一个商店可选可不选,则不选状态可以继续转移到自身(也就是保持),或转移到选。
假设当前状态是选,那么下一商店只能不选,所以选状态只能转移到不选状态,而不能转移到自身。

现在我们根据这个关系重新设计一下DP
状态设计:\(f[i,0/1]\) 表示从 \(1\) 开始到前 \(i\) 家商铺,第 \(i\) 家商铺 不抢/抢 得到的最大价值。
状态计算:\(f[i,0]=max(f[i-1,1],f[i-1,0]),\ f[i,1]=f[i-1,0]+w[i]\)。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10,INF=1e8;
int n,w[N],f[N][2];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
f[0][0]=f[0][1]=0;
for(int i=1;i<=n;i++)
{
f[i][0]=max(f[i-1][1],f[i-1][0]);
f[i][1]=f[i-1][0]+w[i];
}
printf("%d\n",max(f[n][0],f[n][1]));
}
return 0;
}
股票买卖IV
给定一个长度为 \(N\) 的数组,数组中的第 \(i\) 个数字表示一个给定股票在第 \(i\) 天的价格。
设计一个算法来计算你所能获取的最大利润,你最多可以完成 \(k\) 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。
输入格式
第一行包含整数 \(N\) 和 \(k\),表示数组的长度以及你可以完成的最大交易数量。
第二行包含 \(N\) 个不超过 \(10000\) 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
\(1≤N≤10^5, 1≤k≤100\)
输入样例1
3 2
2 4 1
输出样例1
2
输入样例2
6 2
3 2 6 5 0 3
输出样例
2
7
样例解释
样例1:在第 \(1\) 天 (股票价格 \(= 2\)) 的时候买入,在第 \(2\) 天 (股票价格 \(= 4\)) 的时候卖出,这笔交易所能获得利润 \(= 4-2 = 2\) 。
样例2:在第 \(2\) 天 (股票价格 \(= 2\)) 的时候买入,在第 \(3\) 天 (股票价格 \(= 6\)) 的时候卖出, 这笔交易所能获得利润 \(= 6-2 = 4\) 。随后,在第 \(5\) 天 (股票价格 \(= 0\)) 的时候买入,在第 \(6\) 天 (股票价格 \(= 3\)) 的时候卖出, 这笔交易所能获得利润 \(= 3-0 = 3\) 。共计利润 \(4+3 = 7\)。
解析
我们的手里只有有股票和没股票两种状态。
那么买入卖出的操作相当于在两个状态之间转移。
每一天,我们都可以选择卖掉股票或买入股票。
假设我们现在有股票,那么我们可以选择卖出它或继续持有。
假设我们现在没有股票,那么我们可以选择继续没有或买入股票。
本题状态机如下:

据此,我们可以设计DP:
状态设计:\(f(i,j,0/1)\) 为进行了 \(j\) 次交易下第 \(i\) 天 没有股票/有股票 能获得的最大钱数。
状态计算:\(f(i,0)=max(f(i-1,j,0),f(i-1,j-1,1)+w_i)\ ,\ f(i,1)=max(f(i-1,j,0)-w_i,f(i-1,j,1))\)
我们发现每次的状态转移只涉及到第 \(i,i-1\) 层的状态,可以加一个压维优化。
code(未压维)
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int f[N][110][2];
int n,k,w[N];
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
memset(f,-0x3f, sizeof f);
for(int i=0;i<=n;i++) f[i][0][0]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=k;j++)
{
f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]+w[i]);
f[i][j][1]=max(f[i-1][j-1][0]-w[i],f[i-1][j][1]);
}
}
int ans=0;
for(int i=1;i<=k;i++)
ans=max(ans,max(f[n][i][1],f[n][i][0]));
printf("%d",ans);
return 0;
}
股票购买V
给定一个长度为 \(N\) 的数组,数组中的第 \(i\) 个数字表示一个给定股票在第 \(i\) 天的价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 \(1\) 天)。
输入格式
第一行包含整数 \(N\),表示数组长度。
第二行包含 \(N\) 个不超过 \(10000\) 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
\(1≤N≤10^5\)
输入样例
5
1 2 3 0 2
输出样例
3
解析
本题只比上题多了一个条件:每卖出一次股票就会进入冷冻期。卖完股票就会转移到冷冻期状态,而卖股票也要冷冻期过了才能买。
我们再在上一题基础上新增一个冷冻状态即可。根据题目描述画出状态机模型:

根据这个状态机模型,我们就可以直接设计出 DP 了。
-
状态设计:
设 \(f(i,0/1/2)\) 为第 \(i\) 天处于 无股票/冷冻期/有股票 的状态能得到的最大价值。
-
状态计算:
\(f(i,0)=max(\ f(i-1,1),f(i-1,0)\ )\)
\(f(i,1)=f(i-1,2)+w_i\)
\(f(i,2)=max(f(i-1,2),f(i-1,0)-w_i)\)
code
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10,INF=1e8;
int f[N][3],w[N],n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
f[0][0]=0,f[0][1]=-INF,f[0][2]=-INF;
for(int i=1;i<=n;i++)
{
f[i][0]=max(f[i-1][0],f[i-1][1]);
f[i][1]=f[i-1][2]+w[i];
f[i][2]=max(f[i-1][2],f[i-1][0]-w[i]);
}
printf("%d",max(f[n][1],f[n][0]));
return 0;
}
设计密码
你现在需要设计一个密码 \(S\),\(S\) 需要满足:
\(S\) 的长度是 \(N\);
\(S\) 只包含小写英文字母;
\(S\) 不包含子串 \(T\);
例如:\(abc\) 和 \(abcde\) 是 \(abcde\) 的子串,\(abd\) 不是 \(abcde\) 的子串。
请问共有多少种不同的密码满足要求?
由于答案会非常大,请输出答案模 \(10^9+7\) 的余数。
输入格式
第一行输入整数 \(N\),表示密码的长度。
第二行输入字符串 \(T\),\(T\)中只包含小写字母。
输出格式
输出一个正整数,表示总方案数模 \(10^9+7\) 后的结果。
数据范围
\(1≤N≤50\ 1≤|T|≤N\),\(|T|\) 是 \(T\) 的长度。
输入样例1:
2
a
输出样例1:
625
输入样例2:
4
cbc
输出样例2:
456924
解析
提高组要这玩意那我直接做不来,而且说实话这个题很容易往组合数学的方向去想。
我们能够依靠的只有一个子串,很容易 (并不) 想到根据这个信息来设计 DP。
假设现在在构造密码的第 \(i\) 位,与题目中给出的模式串匹配到了第 \(j\) 位,此时这个位置上有 \(26\) 种状态,分别对应 \(26\) 个字母。
那么什么样的方案是可行的?题目中的描述是不包含子串,在 KMP 字符串匹配中就是 \(j\) 不会遍历到最后一位。
我们回顾一下 KMP 的匹配过程:
/*s[i]是文本串,p[i]是模式串*/
for(int i=1,j=0; i<=m; i++)
{
while(j&&s[i]!=p[j+1]) j=next_[j];
if(s[i]==p[j+1]) j++;
if(j==n)
{
cout<<i-n<<" ";
j=next_[j];
}
}
无论是在 \(j\) 向前跳还是向后走的过程中,\(i\) 都是不变的。换个说法,对于一个特定的模式串,\(j\) 能跳到什么位置,完全取决于当前的 \(i\) 的取值如何。\(i\) 的取值有 \(26\) 种,我们可以枚举当前位为 \(a\to z\) ,得到第 \(i\) 位取 \(a\) 时 \(j\) 能到什么地方,取 \(b\) 时 \(j\) 能到什么地方 \(\cdots\cdots\) 取 \(z\) 时 \(j\) 能到什么地方。每枚举一个取值都相当于有一条边连向一个状态,所以这是一个 \(m+1\) 个点,每个点有 \(26\) 边的状态机。
这个状态机就非常复杂了,我们要用循环来完成这个事情。
我们暴力枚举转移来的状态,时间复杂度 \(O(26N^3)\) ,没有任何问题。
-
状态设计:
\(f(i,j)\) 表示构造 \(i\) 长度的密码串,且与题目给出的字符串匹配到 \(j\) 位的方案数量。
-
状态计算:
\(f(i+1,t)=\sum\limits_{k\in \{a,b,\dots ,z\}} f(i,j)\) ,即枚举第 \(i\) 位上的字符 \(k\) 为 \(a\to z\) ,所有能匹配到的位置 \(t\) 上的状态之和。类似于刷表法,每个状态 \(f(i,j)\) 将它能够更新到的 \(f(i+1,t)\) 更新。
#include <bits/stdc++.h>
using namespace std;
const int N=100,mod=1e9+7;
char ch[N];
int f[N][N],nxt[N];
int n;
int main()
{
cin>>n>>(ch+1);
int m=strlen(ch+1);
for(int i=2,j=0;i<=m;i++)
{
while(j&&ch[i]!=ch[j+1]) j=nxt[j];//不相等则退回一位
if(ch[i]==ch[j+1]) ++j;//相等则携手共进
nxt[i]=j;//nxt[i]:以 i 为终点的后缀与前缀相等的最长长度
}
f[0][0]=1;
for(int i=0;i<n;i++)//枚举构造的位数
{
for(int j=0;j<m;j++)//枚举匹配到的位置
{
for(char k='a';k<='z';k++)//枚举这个位置上的取值
{
int tmp=j;//小心不要把枚举的 j 修改掉了
while(tmp && k !=ch[tmp+1]) tmp=nxt[tmp];//回跳
if(k==ch[tmp+1]) ++tmp;//向下匹配
if(tmp<m) f[i+1][tmp]=(f[i+1][tmp]+f[i][j])%mod;//累加方案数
}
}
}
int res=0;
for(int i=0;i<m;i++) res=(res+f[n][i])%mod;
cout<<res;
return 0;
}
修复DNA(坑)
AC 自动机+状态机DP
先挖坑,等我把这玩意做出来了再写。

