数学知识整理及部分例题2
组合数学
本章主要以讲例题为主,聚焦于做题时的思路。
牡牛和牝牛
1s/64M
约翰要带 \(N\) 只牛去参加集会里的展示活动,这些牛可以是牡牛,也可以是牝牛。
牛们要站成一排,但是牡牛是好斗的,为了避免牡牛闹出乱子,约翰决定任意两只牡牛之间至少要有 \(K\) 只牝牛。
请计算一共有多少种排队的方法,所有牡牛可以看成是相同的,所有牝牛也一样,答案对 \(5000011\) 取模。
输入格式
一行,输入两个整数 \(N\) 和 \(K\)。
输出格式
一个整数,表示排队的方法数。
数据范围
\(1≤N≤10^5\\ 0≤K<N\)
输入样例:
4 2
输出样例:
6
解析
简单计数 DP 。
我们将牛序列抽象为 01 序列,牡牛为 1 。
我们设状态 \(f(i)\) 表示所有长度是 \(i\) 的且以 \(1\) 结尾的序列方案数量。
我们可以得到,状态从 \(f(0)\sim f(i-k-1)\) 转移而来。
具体的说,\(f(i)=\sum\limits_{q=0}^{i-k-1}f(q)\) 。
现在我们求出来了所有结尾为 1 的序列数量,但是题目中并没有这一限制,我们还要想办法转化。
最后的 DP,相当于将所有的方案按照最后一个 1 的位置分了类。
也就是我们再前缀和滚一遍就好了。
方程的解
佳佳碰到了一个难题,请你来帮忙解决。
对于不定方程 \(a_1+a_2+⋯+a_{k−1}+a_k=g(x)\),其中 \(k≥1\) 且 \(k\in N^+\),\(x\) 是正整数,\(g(x)=x^x \mod1000\)(即 \(x^x\) 除以 \(1000\) 的余数),\(x,k\) 是给定的数。
我们要求的是这个不定方程的正整数解组数。
举例来说,当 \(k=3,x=2\) 时,方程的解分别为:
输入格式
有且只有一行,为用空格隔开的两个正整数,依次为 \(k,x\)。
输出格式
有且只有一行,为方程的正整数解组数。
数据范围
\(1≤k≤100,\\ 1≤x<2^{31},\\ k≤g(x)\)
输入样例:
3 2
输出样例:
3
解析
\(g(x)=x^x\mod 1000\),非常奇怪的函数。
但是我们可以直接快速幂。算算也才 \(O(\log x)\),就加上一个最多 \(31\) 的常数而已,忽略不计。
说白了,问题就是 \(a_1+a_2+\cdots +a_k=N\) 的正整数解的组数。\(A\) 是常数。
换个模型来描述这个方程:有 \(N\) 个球, 我们要把它们全部放到 \(k\) 个盒子里面,每个盒子至少一个。
这还不简单?我们可以插板法,总共有 \(N-1\) 个空位,我们要选出 \(k-1\) 个空位插上板子,得到 \(k\) 组球,从左到右对应 \(a_1,a_2,a_3\cdots a_k\) 的值。答案即是 \(C_{N-1}^{k-1}\)。
我们甚至可以直接递推计算。
很不幸的是这个题要写高精度。
车的放置
1s/64M
有下面这样的一个网格棋盘,\(a,b,c,d\) 表示了对应边长度,也就是对应格子数。
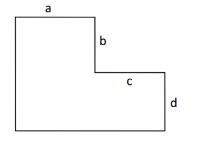
当 \(a=b=c=d=2\) 时,对应下面这样一个棋盘:
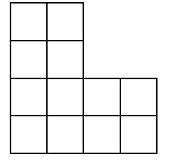
要在这个棋盘上放 \(k\) 个相互不攻击的车,也就是这 \(k\) 个车没有两个车在同一行,也没有两个车在同一列,问有多少种方案。
只需要输出答案 \(\mod100003\) 后的结果。
输入格式
共一行,五个非负整数 a,b,c,d,k。
输出格式
包括一个正整数,为答案 \(\mod100003\) 后的结果。
数据范围
\(0≤a,b,c,d,k≤1000\)
保证至少有一种可行方案。
输入样例
2 2 2 2 2
输出样例
38
解析
我们手模一下样例,发现它的方案数非常多,情况非常复杂。
我们要想想能否对方案进行某种分类,然后应用计数原理。
先对样例中的情况进行分析:

逐行来看:
第一行有 \(2\) 种放法。
第二行,如果第一行放了,就只有 \(1\) 种方法,但是第一行有两种放法,还可以直接不放,情况愈发复杂了。
直接做不大现实,看看能否拆分。
我们将整个图形分割成两个规则图形。

问题就变成了在一个矩形中怎么放车的问题。
假设我们要在一个 \(3\times 4\) 的网格里面放两个车。
我们首先要在 \(3\) 行里面选 \(2\) 行来放,也就是 \(C^2_3\)。
此时,我们选出的第一行就有 \(4\) 种选法。第二行就有 \(3\) 种选法。说的更一般些,我们要在这 \(4\) 列里面选出两列来,由于两行意义不同,所以是排列。
也就是 \(C^2_3\times A^2_4\) 。
那么,如果给一个 \(n\times m\) 的矩阵,让我们放 \(k\) 个车,答案就应该是 \(C_n^k\times A_m^k\)
所以我们可以枚举两个矩阵分别放了多少个车,然后合并方案。那么如何合并上半部分和下半部分的方案呢?
我们人为规定,先放完上半部分再放下半部分。然后我们发现,上半部分对下半部分的影响是一定的,都只占用了 \(i\) 行。也就是说我们只需要在选列的时候,只能用 \(m-i\) 列, \(A_{m-i}^{k-i}\)。
由于我们规定这是分步计数过程,两部分可以直接相乘。
代入题目数据,答案就是 \(\sum\limits_{i=1}^kC_b^i\cdot A_a^i\cdot C_{d}^{k-i}\cdot A_{a+c-i}^{k-i}\quad(\mod100003)\)。
code(轻度压行)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010,mod=100003;
ll fac[N],infa[N];//阶乘,阶乘逆元
ll fpow(ll a,ll k)
{
ll res=1;
while(k){if(k&1) res=(ll)res*a%mod; a=a*a%mod; k>>=1;}
return (res+mod)%mod;
}
void init()
{
fac[0]=infa[0]=1;
for(int i=1;i<=N-10;++i)
{
fac[i]=(ll)fac[i-1]*i%mod;
infa[i]=(ll)infa[i-1]*fpow(i,mod-2)%mod;
}
}
inline ll C(ll a,ll b) {if(a<b) return 0; return fac[a]*infa[b]*infa[a-b]%mod;}// C_a^b
inline ll A(ll a,ll b) {if(a<b) return 0; return fac[a]*infa[a-b]%mod;}
int main()
{
init();
ll a,b,c,d,k;
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
ll ans=0;
for(int i=0;i<=k;i++)
{
ans+=(ll)C(b,i)*A(a,i)%mod*C(d,k-i)*A(a+c-i,k-i)%mod;
ans%=mod;
}
printf("%lld",(ans+mod)%mod);
return 0;
}
数三角形
给定一个 \(n×m\) 的网格,请计算三点都在格点上的三角形共有多少个。
下图为 \(4×4\) 的网格上的一个三角形。
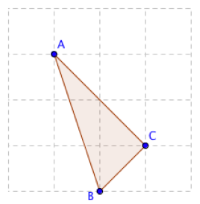
注意:三角形的三点不能共线。
输入格式
输入一行,包含两个空格分隔的正整数 \(m\) 和 \(n\)。
输出格式
输出一个正整数,为所求三角形数量。
数据范围
\(1≤m,n≤1000\)
输入样例:
2 2
输出样例:
76
解析
让我们在一个 \(n\times m\) 的网格内选三个点,要求它们不共线。为了方便,下面的 \(n,m\) 描述的都是格点的行列。
直接求合法方案数实在不大好求,正难则反,我们考虑求不合法的方案数。
我们总共的方案数 \(C_{nm}^3\),现在要排除三点共线的所有方案。
将这个网格图看做一个坐标系,\((i,j)\) 表示在第 \(i\) 行第 \(j\) 列,左下角是 \((0,0)\)。所有的直线按照斜率 \(k\) 的情况分为 \(4\) 种:\(k>0\) 的,\(k<0\) 的,\(k=0\) 的,\(k=tan90^{\circ}\) 的。
分别来看这些情况。
-
\(k=0\)
总共共有 \(n\) 行,每行都可以选 \(3\) 个,根据计数原理,这种情况的方案数为 \(nC_m^3\)。
-
\(k=tan90^{\circ}\)
总共 \(m\) 列,每列都可以选 \(3\) 个,方案数为 \(mC_n^3\)。
-
\(k>0\)
我们按照这三个点中最左边的点,将所有的方案分成 \(n\times m\) 类。假设当前左下角在 \((i,j)\) 这个点,要求它的方案数。两点确定一条直线,我们再枚举最右边的点,看看有多少种情况
画画图:

此时右上角的选法就有 \((m-i)(n-j)\) (注意这里横纵坐标的定义与我们习惯的相反)
现在我们要确定的是,对于一个确定的右上角的点,构成的直线上有多少个点。
设它们的横纵坐标差为 \(i_0,j_0\) ,若起点终点都是整点,则它们之间的整点数有 \(gcd(i_0,j_0)-1\) 个(不包括端点)。
为啥?
我们把它看做一个向量,将它平移到源点,也就是考虑 \((0,0)\) 到 \((i,j)\) 上的点,我们可以得到它的斜率是 \(\frac{i}{j}\) 。将其化简到最简整数比,就是除以 \(gcd(i,j)\)。我们知道,假如一个直线的斜率是 \(\frac{2}{3}\) 且存在一个 \((x_0,y_0)\) 在直线上,那 \((x_0+2k,y_0+3k)\) 都是整数点。在上文所述的向量中,假设化为最简整数比的分数是 \(\frac{i^{\prime}}{j^{\prime}}\) ,那么有 \(i^{\prime}\cdot gcd(i,j)=i,j^{\prime}\cdot gcd(i,j)=j\) ,那么这个向量上就有 \(gcd(i,j)\) 这个答案算上了右端点。再减去就是 \(gcd(i,j)-1\)。
这个结论在我们所习惯的平面直角坐标系中也能够成立。
总之,我们的答案就是 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^mgcd(i,j)(m-i)(n-j)\)
-
\(k<0\)
由对称性可知,同 \(k>0\)。
综上,我们的答案是:
总的复杂度 \(O(n^2\log n)\),上界宽松,能过。
当然,这个题还可以继续使用莫比乌斯反演达到 \(O(n)\),这里就不搞了。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) {return b==0?a:gcd(b,a%b);}
ll C(ll x) {return (ll)x*(x-1)*(x-2)/6ll;}
int main()
{
ll n,m;
scanf("%lld%lld",&n,&m);
++n,++m;
ll ans=C(n*m)-n*C(m)-m*C(n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
ans-=2ll*(gcd(i,j)-1)*(n-i)*(m-j);
}
printf("%lld",ans);
return 0;
}
积性函数
积性函数是一个针对数论函数的概念
积性函数:对于 \(\forall a,b,\ gcd(a,b)=1\Rightarrow f(ab)=f(a)f(b)\) 则称 \(f\) 是一个积性函数。
若对于 \(\forall a,b\in N\) 都成立则称 \(f\) 为完全积性函数。
所有的积性函数都可以用线筛求。
一些常用的积性函数:
- \(\varphi\): 欧拉函数
- \(\mu\): 莫比乌斯函数
- \(f(x)=gcd(x,k),k\text{为常数}\): 其中一个数确定的最大公约数
- \(d(n)\): \(n\) 的正约数个数
- \(\sigma(n)\): \(n\) 的正约数和。
- \(I(n)=1\): 常函数。(完全积性)
- \(id(n)=n\): 单位函数。(完全积性)
- \(\epsilon(n)=\begin{cases}1,&n=1\\ 0,&n>1\end{cases}\) : 狄利克雷卷积乘法单元。(完全积性)
Longge的问题
1s/64M
求 \(\sum\limits_{i=1}^ngcd(i,n)\) 的值。
输入格式
一个整数 \(n\)
输出格式
一个整数表示答案。
数据范围
\(1<n<2^{31}\)
输入样例
6
输出样例
15
解析
套路地假设 \(gcd(x,n)=d\),那么 \(gcd(\frac{x}{d},\frac{n}{d})=1\) 。
我们枚举 \(n\) 的因子 \(d\) ,直接求有多少个 \(x\) 满足 \(gcd(x,n)=d\) 。
也就是我们要求 \(\sum\limits_{x=1}^{n/d}d\cdot [gcd(\frac{x}{d},\frac{n}{d})=1]\)
我们发现提个公因式之后这就是欧拉函数的定义。
所以答案就是 \(\sum\limits_{d|n}d\cdot \varphi(\frac{n}{d})\) 。
到这里已经可以勉强可以做了。\(n\) 的因子数最多不过 \(1600\) ,再 \(\sqrt n\) 分解质因数暴力求解 \(\varphi\) 大概能过。
但是我们不满足。
继续推式子,我们让 \(\frac{n}{d}=d^{\prime}\),并由质因数分解设 \(d^{\prime}=\prod\limits_{i=1}^kp_i^{c_i}\) 。
我们再设 \(n=\prod\limits_{i=1}^k p_i^{\alpha_i},d=\prod\limits_{i=1}^k p_i^{\beta_i}\) ,其中 \(0\le \beta_i\le \alpha_i\)。
可以知道,n的任何一个约数都能表示成这样一个形式。
这样我们就可以表示 \(n\) 的所有约数了。
对于我们一个确定的约数 \(d^{\prime}\) ,我们只需要看它的哪些因数的指数是 \(\ge 1\) 的,将它们乘积,在加起来就是答案。
听起来还是和暴力差不多,我们要想一想怎么做。
从另外一个角度思考,假设我们要求所有因子的乘积,由于我们要枚举所有的因子,所以对于每个因子 \(p_{k}\) 必然被选中一次,二次,三次……直到 \(\alpha_k\) 次。再根据计数原理,得到:
由此作为启发,我们将上面的方法对应下来得到:
展开化简,得到:
也就是说,\(O(\sqrt n)\) 分解质因数即可。
code极短:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n;
cin>>n;
ll res=n;
for(ll i=2LL;i*i<=n;++i)
{
if(n%i==0)
{
ll a=0,p=i;
while(n%p==0) ++a,n/=p;
res/=p;
res=res*(p+(ll)a*p-a);//算答案
}
}
if(n>1) res/=n,res=res*((ll)n+n-1LL);
cout<<res;
return 0;
}
狄利克雷卷积
狄利克雷卷积是一个对数论函数集合封闭的二元计算,即两个数论函数的卷积还是数论函数。
设 \(f,g\) 是两个数论函数,它们的卷积为 \((f*g)(n)=\sum\limits_{d|n}f(d)g(\frac{n}{d})\) 。
我们可以借此再次描述一下莫比乌斯反演:
若 \(F=f*I\),则 \(f=F *\mu\)。
狄利克雷卷积的性质
- 满足交换律和结合律。
- 若 \(f,g\) 都是积性函数,那么 \(f * g\) 仍然是积性函数。反之,若 \(f,f *g\) 都是积性函数,那么 \(g\) 也是积性函数。
- 若 \(g\) 是一个完全积性函数,且 \(h=f*g\),则 \(f=h * (\mu g)\) ,即若:\[h(n)=\sum_{d|n}f(d)g(\frac{n}{d}) \]则:\[f(n)=\sum_{d|n}h(d)\mu(\frac{n}{d})g(\frac{n}{d}) \]
常用的狄利克雷卷积等式
- \(\mu*I=\epsilon\)
- \(\varphi*I=id\)
- \(\mu*id=\varphi\)

