联考20200725 T2 Tree


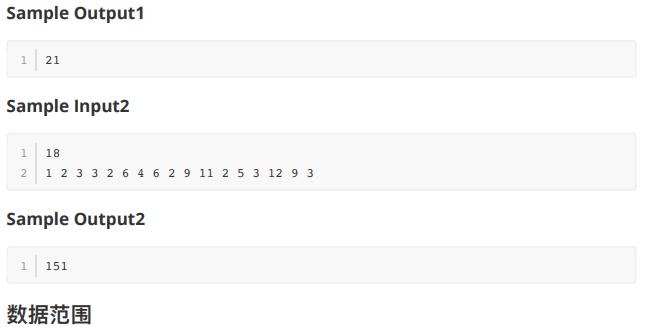
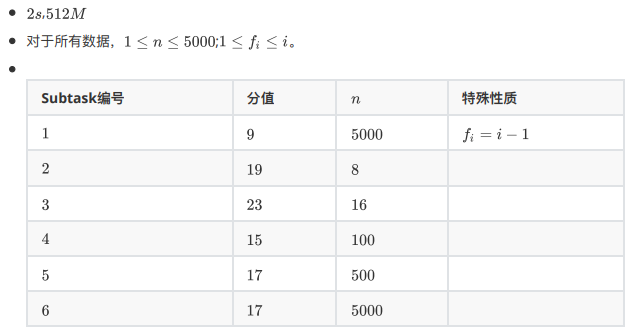
分析:
神仙DP,又被开除人籍了
整个过程是LCT逆过程?(雾)
设状态\(f_{i,j}\)表示以\(i\)号点为根,构成一棵大小为\(j\)的二叉树变换为一条链的整棵子树的最大深度
画个图便于理解:
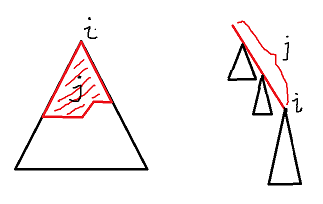
考虑如何转移,一个点\(i\)作为根的二叉树在中序遍历情况下,它的左子树全部节点会成为\(i\)的祖先,对\(i\)和子树内剩下节点的深度造成影响
右子树会成为\(i\)的后代,不会影响其余点的深度,但是其大小会统计到\(i\),以便再向上DP
然后剩下的儿子会接在\(i\)上,向上统计时全部节点深度加一再加上去就可以了
我们把儿子排成一行,一个一个合并时,在里面选两个作为左右儿子,我们假设左儿子在右儿子前面选

右儿子在左儿子前边的情况倒序做就行了
根节点为\(u\),考虑目前统计到儿子\(v\),想让\(v\)做右儿子,大小为\(j\)
那么要在\(v\)前面选出一个左儿子大小为\(i\),且与其他非关键儿子向上合并得到的深度和最大
再开一个数组\(g_{u,i}\)表示,目前\(u\)已经统计过的儿子里,某一个大小为\(i\)的子树作为左儿子,与其他非关键儿子向上合并得到的深度和的最大值
这两个dp值可以同时维护
还要注意一下一个点没有右儿子的情况,处理左儿子时直接统计答案
好像有点口胡,还是看代码吧(
复杂度\(O(n^2)\)
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<string>
#define maxn 5005
#define INF 0x3f3f3f3f
#define MOD 998244353
#define eps 1e-10
using namespace std;
inline long long getint()
{
long long num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n;
vector<int>G[maxn];
int f[maxn][maxn],g[maxn][maxn],mx[maxn],sz[maxn];
inline void dfs(int u)
{
int Sz=0,Sum=0;
for(int i=0;i<G[u].size();i++)
dfs(G[u][i]),Sz+=sz[G[u][i]],Sum+=mx[G[u][i]];
f[u][1]=g[u][0]=Sum;
for(int i=0;i<G[u].size();i++)
{
int v=G[u][i];
for(int i=0;i<=sz[u];i++)for(int j=1;j<=sz[v];j++)
f[u][i+j+1]=max(f[u][i+j+1],g[u][i]+f[v][j]-mx[v]+sz[v]+i);
sz[u]+=sz[v];
for(int i=1;i<=sz[v];i++)
g[u][i]=max(g[u][i],Sum+f[v][i]-mx[v]+i*(Sz-sz[v])),
f[u][i+1]=max(f[u][i+1],Sum+f[v][i]-mx[v]+i*(Sz-sz[v]));
}
memset(g[u],-INF,sizeof g[u]);
g[u][0]=Sum,sz[u]=0;
for(int i=G[u].size()-1;~i;i--)
{
int v=G[u][i];
for(int i=0;i<=sz[u];i++)for(int j=1;j<=sz[v];j++)
f[u][i+j+1]=max(f[u][i+j+1],g[u][i]+f[v][j]-mx[v]+sz[v]+i);
sz[u]+=sz[v];
for(int i=1;i<=sz[v];i++)
g[u][i]=max(g[u][i],Sum+f[v][i]-mx[v]+i*(Sz-sz[v])),
f[u][i+1]=max(f[u][i+1],Sum+f[v][i]-mx[v]+i*(Sz-sz[v]));
}
sz[u]++;
for(int i=1;i<=sz[u];i++)mx[u]=max(mx[u],f[u][i]);
mx[u]+=sz[u];
}
int main()
{
n=getint();
for(int i=2;i<=n;i++)G[getint()].push_back(i);\
memset(f,-INF,sizeof f),memset(g,-INF,sizeof g);
dfs(1);
printf("%d\n",mx[1]);
}

