联考20200722 T2 ACT4！无限回转！

分析：
倒过来思考，我们求某条直线的概率时，选择一个角度确定，那么选到做贡献的点的概率为下图着色面积与总面积之比：

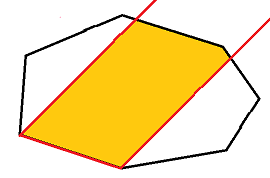
着色面积可以先求半平面覆盖面积然后作差
半平面覆盖面积极角排序二分找到相交线段计算
然而角度也是不确定的，但是我们发现以角度为自变量，得到的概率函数是连续的
其实可以看做一个概率密度函数，我们可以求积分得到具体概率
函数貌似不平滑，但是求的是近似值，我们使用辛普森积分就可以解决
复杂度\(O(n^2+n\sigmalogn)\)
其中\(\sigma\)为一次辛普森积分的复杂度

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<string>

#define maxn 100005
#define INF 0x3f3f3f3f
#define MOD 998244353
#define eps 1e-10

using namespace std;

inline long long getint()
{
	long long num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

const double pi=acos(-1);
int n;
double simpeps;
double ang[maxn],sum[maxn];
struct pt{
	double x,y;
	pt(){}pt(double _x,double _y){x=_x,y=_y;}
	friend pt operator +(pt x,pt y){return pt(x.x+y.x,x.y+y.y);}
	friend pt operator -(pt x,pt y){return pt(x.x-y.x,x.y-y.y);}
}p[maxn];
inline double atan2(pt a){return atan2(a.y,a.x);}
struct line{pt a,b;};

inline double Cross(pt x,pt y)
{return x.x*y.y-x.y*y.x;}
inline pt inter(line a,line b)
{
	double s1=Cross(b.a-a.a,b.b-a.a),s2=Cross(b.b-a.b,b.a-a.b);
	return pt(a.a.x+(a.b.x-a.a.x)/(s1+s2)*s1,a.a.y+(a.b.y-a.a.y)/(s1+s2)*s1);
}
inline double calc(double x)
{
	int q=upper_bound(ang+1,ang+n+1,x)-ang-1;
	double ans=sum[q];
	if(q>=n||fabs(x-ang[n])<eps)return ans;
	if(q==1||fabs(x-ang[2])<eps)return 0;
	line l=(line){p[1],p[1]+pt(cos(x),sin(x))};
	pt P=inter((line){p[q],p[q%n+1]},l);
	ans+=Cross(P-p[1],p[q]-p[1]);
	return ans;
}

inline double calc(double dx,double y1,double y2,double y3)
{return (y1+4*y2+y3)*dx/6;}
inline double simp(double l,double r,double mid,double yl,double yr,double ymid,double c)
{
	double lm=(l+mid)/2,ylm=calc(lm);
	double rm=(r+mid)/2,yrm=calc(rm);
	double c1=calc(mid-l,yl,ylm,ymid),c2=calc(r-mid,ymid,yrm,yr);
	if(abs(c1+c2-c)<simpeps)return c1+c2;
	return simp(l,mid,lm,yl,ymid,ylm,c1)+simp(mid,r,rm,ymid,yr,yrm,c2);
}
inline double getp(double l,double r)
{return simp(l,r,(l+r)/2,calc(l),calc(r),calc((l+r)/2),calc(r-l,calc(l),calc(r),calc((l+r)/2)));}

int main()
{
	n=getint();
	for(int i=1;i<=n;i++)p[i].x=getint(),p[i].y=getint();
	double S=0;
	for(int i=1;i<=n;i++)S+=Cross(p[i],p[i%n+1]);
	simpeps=eps*S;
	for(int t=1;t<=n;t++)
	{
		for(int i=2;i<=n;i++)
		{
			ang[i]=atan2(p[i]-p[1]);
			if(i>2)
			{
				while(ang[i]<ang[2])ang[i]+=pi*2;
				while(ang[i]>ang[2]+pi)ang[i]-=pi*2;
			}
			sum[i]=sum[i-1]+Cross(p[i]-p[1],p[i-1]-p[1]);
		}
		sum[n+1]=sum[n],ang[1]=-2*pi;
		double simp1=getp(ang[2],ang[2]+pi);p[n+1]=p[1];
		for(int i=1;i<=n;i++)p[i]=p[i+1];
		ang[n]=atan2(p[n]-p[1]);
		for(int i=2;i<n;i++)
		{
			ang[i]=atan2(p[i]-p[1]);
			while(ang[i]<ang[n])ang[i]+=pi*2;
			while(ang[i]>ang[n]+pi)ang[i]-=pi*2;
			sum[i]=sum[i-1]+Cross(p[i]-p[1],p[i-1]-p[1]);
		}
		sum[n+1]=sum[n],ang[1]=-2*pi;
		double simp2=getp(ang[n]-pi,ang[n]);
		printf("%.10lf\n",(simp2-simp1)/(S*pi*2));
	}
}