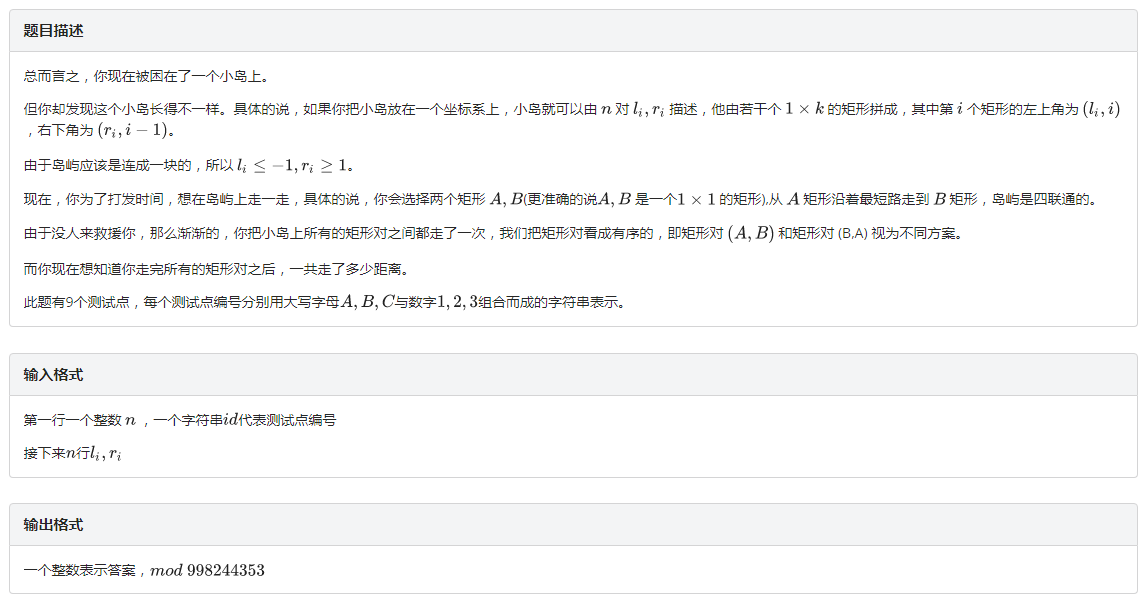
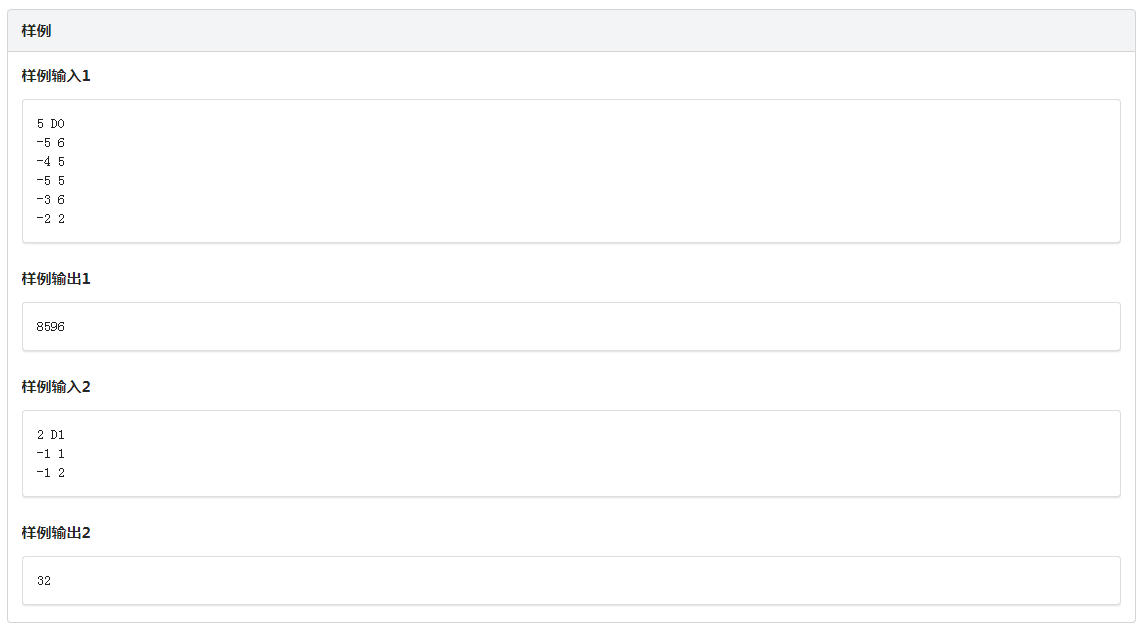
联考20200521 T1 island

分析：
（流下了没有数理基础的泪水.jpg）
真就神仙分类讨论+推导呗

求一下纵向的贡献，通过O(n)枚举分割线乘以两端的组合方案数
求一下横向跨象限的贡献，求每个点到y轴的距离（这个是一次函数求和）乘以方案数（这里的方案数乘以的是对面象限的方案，再乘上同象限的方案是为了方便统计下面1,2的方案）

然后求同象限方案数
一对点（A,B）的方案为L[A]+L[B]-2*L[X]
X为其间最小的距离
使用单调栈构造笛卡尔树
对于一段区间，我们已知它最低点的位置m和高度h
令getsum(x)为一维前缀和，getspw(x)为二维前缀和

1、计算左半部分超出h的对右半部分超出h向下延伸的贡献（黄绿组合）
可以在穿过象限的时候统计，在笛卡尔树中只需要减去最低点的贡献（getsum(x)乘上左边的大小）
2、计算右半部分超出h的对左半部分超出h向下延伸的贡献（黄绿组合）
可以在穿过象限的时候统计，在笛卡尔树中只需要减去最低点的贡献（getsum(x)乘上右边的大小）
3、计算左半部分超出h的对右半部分不超出h向下延伸的贡献（黄橙组合）
\(getspw(a[mid])*(r-mid)-getsum(a[mid])*(r-mid)*(a[mid]+1)\)
4、计算右半部分超出h的对左半部分不超出h向下延伸的贡献（绿蓝组合）
\(getspw(a[mid])*(mid-l)-getsum(a[mid])*(mid-l)*a[mid]\)
5、计算左半部分没有超出h（假设目前高度为x）对右半部分超出x不超过h的贡献（左低右高）（蓝橙组合）
列出暴力求和的式子，化出来是\(getspw(x)*(r-mid+1)*（mid-l）\)
6、计算右半部分没有超出h（假设目前高度为x）对左半部分超出x不超过h的贡献（左高右低）（蓝橙组合）
列出暴力求和的式子，化出来是\(getspw(x)*(r-mid)*（mid-l+1）\)
7、计算m该位置上对两端不含位置m的贡献（紫色向外）
\((sum[mid]-sum[l-1])+(mid-l+1)*(a[mid]+1)*((sum[r]-sum[mid-1])+(r-mid+1)*(a[mid]+1))*a[mid]\)
8、计算m该位置对自身的贡献（紫色内部）
\(getspw(x)-x*getsum(x)\)
注意贡献是双向的要乘2

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<iostream>
#include<map>
#include<string>

#define maxn 1000005
#define MOD 998244353
#define inv2 499122177
#define inv6 166374059

using namespace std;

inline long long getint()
{
	long long num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

int n;
int L[maxn],R[maxn];
int pre[maxn],sub[maxn],sumL,sumR;
int sum[maxn],lc[maxn],rc[maxn];
int ans,stk[maxn],tp;

inline int add(int x,int y){return (x+y)%MOD;}
inline int getsum(int x)
{return 1ll*x*(x+1)%MOD*inv2%MOD;}
inline int getspw(int x)
{return 1ll*x*(x+1)%MOD*add(x,x+1)%MOD*inv6%MOD;}

void Solve(int mid,int l,int r,int *a)
{
	if(l>r)return;
	ans=add(ans,2ll*(MOD-1ll*getsum(a[mid])*((sum[mid]-sum[l-1]+MOD)%MOD-a[mid]-1)%MOD*(r-mid+1)%MOD)%MOD);
	ans=add(ans,2ll*(1ll*getspw(a[mid])*(r-mid+1)%MOD*(mid-l))%MOD);
	
	ans=add(ans,2ll*(MOD-1ll*getsum(a[mid])*(r-mid)%MOD*(a[mid]+1ll)%MOD)%MOD);
	ans=add(ans,2ll*getspw(a[mid])*(r-mid)%MOD);
	
	ans=add(ans,2ll*(MOD-1ll*getsum(a[mid])*(mid-l+1)%MOD*((sum[r]-sum[mid-1]+MOD)%MOD-1ll*a[mid]-1-(1ll*r-mid))%MOD)%MOD);
	ans=add(ans,2ll*getspw(a[mid])*(r-mid)%MOD*(mid-l+1)%MOD);
	
	ans=add(ans,2ll*(MOD-1ll*getsum(a[mid])*(mid-l)%MOD*a[mid]%MOD)%MOD);
	ans=add(ans,2ll*getspw(a[mid])*(mid-l)%MOD);
	
	ans=add(ans,2ll*(MOD-1ll*((sum[mid]-sum[l-1]+MOD)%MOD-1ll*(mid-l+1)*(a[mid]+1)%MOD)*((sum[r]-sum[mid-1]+MOD)%MOD-1ll*(r-mid+1)*(a[mid]+1)%MOD)%MOD*a[mid])%MOD);
	
	Solve(lc[mid],l,mid-1,a);
	Solve(rc[mid],mid+1,r,a);
}

int main()
{
	n=getint(),getint();
	for(int i=1;i<=n;i++)sumL=add(sumL,MOD-(L[i]=getint())),sumR=add(sumR,R[i]=getint());
	for(int i=1;i<=n;i++)pre[i]=add(pre[i-1],add(R[i],-L[i]));
	for(int i=n;i>=1;i--)sub[i]=add(sub[i+1],add(R[i],-L[i]));
	for(int i=1;i<n;i++)ans=add(ans,1ll*pre[i]*sub[i+1]%MOD);
	for(int i=1;i<=n;i++)R[i]--,L[i]=-L[i];
	for(int i=1;i<=n;i++)ans=add(ans,1ll*(pre[n]-1)*add(getsum(R[i]),getsum(L[i]))%MOD);
	
	for(int i=1;i<=n;i++)
	{
		while(tp&&R[stk[tp]]>R[i])rc[stk[tp]]=lc[i],lc[i]=stk[tp],tp--;
		stk[++tp]=i;
		sum[i]=(R[i]+1+sum[i-1])%MOD;
		ans=(ans-2ll*R[i]*getsum(R[i])+2ll*getspw(R[i]))%MOD;
	}
	stk[tp+1]=0;
	while(tp)rc[stk[tp]]=stk[tp+1],tp--;
	Solve(stk[1],1,n,R);
	
	memset(lc,0,sizeof lc);
	memset(rc,0,sizeof rc);
	for(int i=1;i<=n;i++)
	{
		while(tp&&L[stk[tp]]>L[i])rc[stk[tp]]=lc[i],lc[i]=stk[tp],tp--;
		stk[++tp]=i;
		sum[i]=(L[i]+1+sum[i-1])%MOD;
		ans=(ans-2ll*L[i]*getsum(L[i])+2ll*getspw(L[i]))%MOD;
	}
	stk[tp+1]=0;
	while(tp)rc[stk[tp]]=stk[tp+1],tp--;
	Solve(stk[1],1,n,L);
	
	printf("%d\n",(2*ans%MOD+MOD)%MOD);
}