巨坑练习题！！！—— Car的旅行线路

在看题目之前，请童鞋们做好心理准备╮(╯▽╰)╭

题目描述
又到暑假了，住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第I个城市中高速铁路了的单位里程价格为Ti，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为t。那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。任务: 找出一条从城市A到B的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入
第一行为一个正整数n(1≤n≤10)，表示有n组测试数据。

每组的第一行有四个正整数s，t，A，B。 S(0＜S≤100)表示城市的个数，t表示飞机单位里程的价格，A，B分别为城市A，B的序号，(1≤A，B≤S)。

接下来有S行，其中第I行均有7个正整数xi1，yi1，xi2，yi2，xi3，yi3，Ti，这当中的(xi1，yi1)，(xi2，yi2)，(xi3，yi3)分别是第I个城市中任意三个机场的坐标，TI为第I个城市高速铁路单位里程的价格。

输出
共有n行，每行一个数据对应测试数据，结果保留2位小数。

样例输入
1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
样例输出
47.55

让我缓缓，现在看这道题都有心理阴影…………

首先，来看看这道题需要什么技巧:

1、求每个城市第四个飞机场的坐标

2、将每个机场的直线距离求出，乘以火车或飞机的单价

3、遍历图，找最短边

4、输出最小值

5、因有多组数据，所以要初始化

让我们来一个一个的解决吧

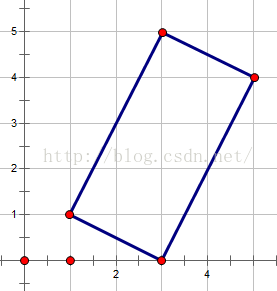
1、首先，试着在直角坐标系上画一个任意四边形，让我们来探究规律，我也画了一个任意四边形：

所以只要确定哪一个是三点之间的直角点，那么与其对应的未知点就可以用以上公式求出来~\(≧▽≦)/~

代码实现实在不行的话，待会儿看样例代码吧~

2、将城市中的四个点求出之后，就直接乘以此城市的火车价，算出dis[ i ][ j ]，最后在同一循环，判断此边是否赋值，如果没有，将两点距离算出来，直接乘以飞机价格 ( 两点间距离公式：AB = sqrt( pow( XA - XB ) + pow( YA - YB ) ) )

3、先复习一下四种算法——>(点击打开链接点击打开链接)首先，Car可以从A城市的任意一个机场到B城市的任意一个机场，所以不确定起点终点，而第2、3、4种算法都要确定起点，所以我们只能用Floyed算法，先来算算时间复杂度（O(n^3)(nmax=400)），明显不会超时，所以，就要这个了！

4、最小值，由于有两个城市，四个点，只需循环16次即可，找出最小的dis[ i ][ j ]，没什么难度

5、初始化只需将每个数组清空就行啦~\(≧▽≦)/~

好了，难点的处理就这些，还有不懂的童鞋，就看看代码吧：

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
struct ill{
	int x,y;
}p[101][5];
int n,plane,A,B,train[101];
double ways[405][405];
void chu(int f)
{
	int i,j;
	for(i=1;i<4;i++)
		for(j=i+1;j<=4;j++)
			ways[(f-1)*4+i][(f-1)*4+j]=ways[(f-1)*4+j][(f-1)*4+i]=sqrt(pow(p[f][i].x-p[f][j].x,2.0)+pow(p[f][i].y-p[f][j].y,2.0))*train[f];
}
void find(int f)
{
	int i,j,k=0,z;
	double l[4];
	for(i=1;i<=2;i++)
		for(j=i+1;j<=3;j++)
		{
			l[6-i-j]=sqrt(pow(p[f][i].x-p[f][j].x,2.0)+pow(p[f][i].y-p[f][j].y,2.0));
			if(k<l[6-i-j])
			{
				k=l[6-i-j];
				z=6-i-j;
			}
		}
	swap(p[f][z].x,p[f][1].x);
	swap(p[f][z].y,p[f][1].y);
	p[f][4].x=p[f][3].x-p[f][1].x+p[f][2].x;
	p[f][4].y=p[f][3].y-p[f][1].y+p[f][2].y;
}
void chu2()
{
	int i,j;
	for(i=1;i<=n*4;i++)
		for(j=1;j<=n*4;j++)
			if(!ways[i][j]&&i-j!=0)
				ways[i][j]=plane*sqrt(pow(p[(i-1)/4+1][(i-1)%4+1].x-p[(j-1)/4+1][(j-1)%4+1].x,2.0)+pow(p[(i-1)/4+1][(i-1)%4+1].y-p[(j-1)/4+1][(j-1)%4+1].y,2.0));
}
void scan()
{
	int i,j;
	scanf("%d%d%d%d",&n,&plane,&A,&B);
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=3;j++)
			scanf("%d%d",&p[i][j].x,&p[i][j].y);
		find(i);
		scanf("%d",&train[i]);
		chu(i);
	}
	chu2();
}
void floyed()
{
	int i,j,k;
	for(k=1;k<=n*4;k++)
		for(i=1;i<=n*4;i++)
			for(j=1;j<=n*4;j++)
				ways[i][j]=min(ways[i][j],ways[i][k]+ways[k][j]);
}
void print()
{
	int i,j;
	double k=1<<30;
	for(i=1;i<=4;i++)
		for(j=1;j<=4;j++)
			k=min(k,ways[(A-1)*4+i][(B-1)*4+j]);
	printf("%.2lf\n",k);
}
void over()
{
	memset(p,0,sizeof(p));
	memset(train,0,sizeof(train));
	memset(ways,0,sizeof(ways));
}
int main()
{
	int nn;
	scanf("%d",&nn);
	for(;nn;nn--)
	{
		scan();
		floyed();
		print();
		over();
	}
}

其实，遇到难题的时候，把它化成几个小问题，逐个击破，难题也就不那么难了

posted @ 2016-11-01 13:58 Izayoi_Doyo 阅读(204) 评论(0) 编辑收藏举报

刷新页面返回顶部

巨坑练习题！！！—— Car的旅行线路

公告