【转载】机器学习-模型融合方法概述
本文转载自【机器学习】模型融合方法概述 - 贝尔塔的文章 - 知乎
转载仅出于个人学习收藏,侵删
我理解的Kaggle比赛中提高成绩主要有3个地方
-
特征工程
-
调参
-
模型融合
之前每次打比赛都只做了前两部分,最后的模型融合就是简单的加权平均,对于进阶的 Stacking 方法一直没尝试,这几天摸索了一下还是把 Stacking 方法给弄懂了。(本文重点讲解 Stacking, Bagging 和 Boosting 有很多权威的好教程,所以不详细介绍)最早的 Stacking 思想早些年就有论文发表,但是应用 Stacking 方法到比赛中的相关文章还是少之甚少,这有两篇kaggle-ensembling-guide/、HUMAN ENSEMBLE LEARNING 讲的很棒,但是之前因为理解不到位,有几处卡住了。在 @Wille 的文章 如何在 Kaggle 首战中进入前 10% 中 Stacking 只是作为一部分提到。因此决定自己写一篇关于模型融合的文章。本文不涉及到各个算法原理层次的深度,目的在于从宏观上帮助理解这几个模型融合方法。
一、Voting
模型融合其实也没有想象的那么高大上,从最简单的 Voting 说起,这也可以说是一种模型融合。假设对于一个二分类问题,有 3 个基础模型,那么就采取投票制的方法,投票多者确定为最终的分类。
二、Averaging
对于回归问题,一个简单直接的思路是取平均。稍稍改进的方法是进行加权平均。权值可以用排序的方法确定,举个例子,比如 A、B、C 三种基本模型,模型效果进行排名,假设排名分别是 1,2,3,那么给这三个模型赋予的权值分别是 3/6、2/6、1/6。
这两种方法看似简单,其实后面的高级算法也可以说是基于此而产生的,Bagging 或者Boosting 都是一种把许多弱分类器这样融合成强分类器的思想。
三、Bagging
Bagging 就是采用有放回的方式进行抽样,用抽样的样本建立子模型,对子模型进行训练,这个过程重复多次,最后进行融合。大概分为这样两步:
-
重复K次
- 有放回地重复抽样建模
- 训练子模型
-
模型融合
- 分类问题:voting
- 回归问题:averaging
Bagging 算法不用我们自己实现,随机森林就是基于 Bagging 算法的一个典型例子,采用的基分类器是决策树。R 和 python 都集成好了,直接调用。
四、Boosting
Bagging 算法可以并行处理,而 Boosting 的思想是一种迭代的方法,每一次训练的时候都更加关心分类错误的样例,给这些分类错误的样例增加更大的权重,下一次迭代的目标就是能够更容易辨别出上一轮分类错误的样例。最终将这些弱分类器进行加权相加。引用加州大学欧文分校 Alex Ihler 教授的两页PPT。
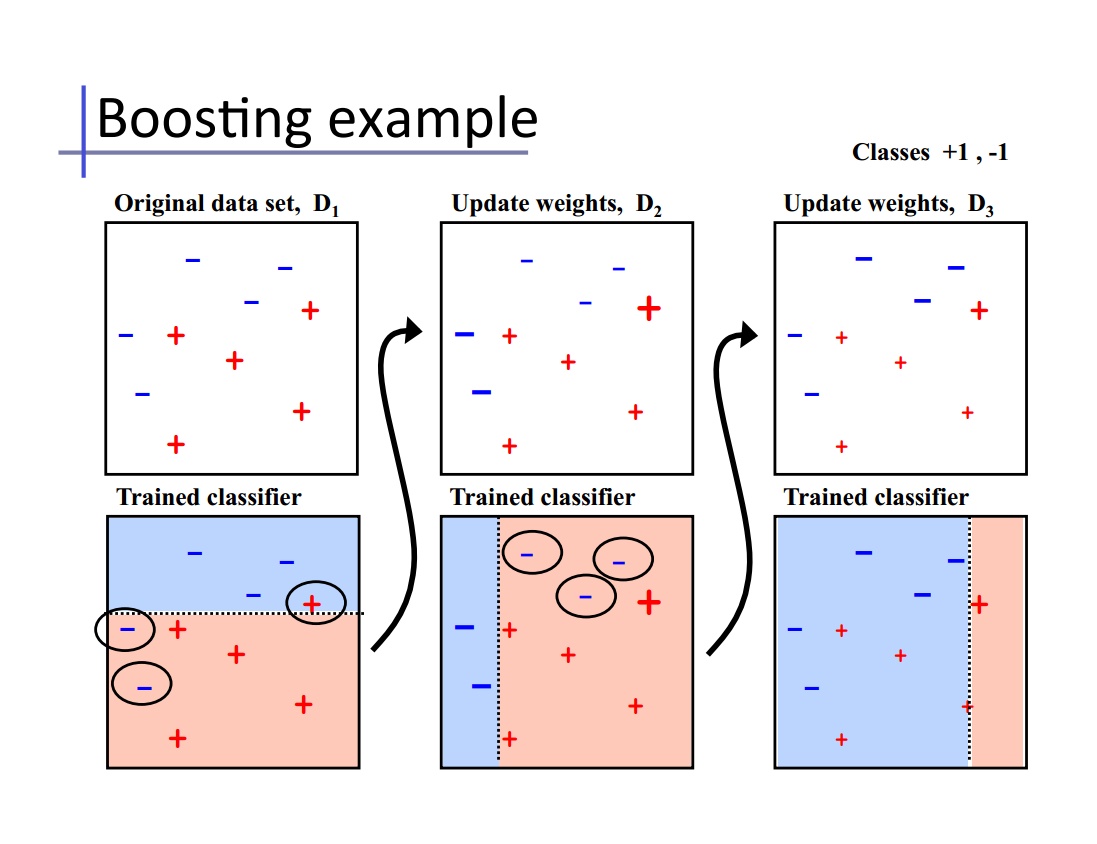

同样地,基于 Boosting 思想的有 AdaBoost、GBDT 等,在 R 和 python 也都是集成好了直接调用。
PS:理解了这两点,面试的时候关于 Bagging、Boosting 的区别就可以说上来一些,问 Randomforest 和 AdaBoost 的区别也可以从这方面入手回答。也算是留一个小问题,随机森林、Adaboost、GBDT、XGBoost 的区别是什么?
五、Stacking
Stacking 方法其实弄懂之后应该是比 Boosting 要简单的,毕竟小几十行代码可以写出一个 Stacking 算法。我先从一种“错误”但是容易懂的 Stacking 方法讲起。
Stacking 模型本质上是一种分层的结构,这里简单起见,只分析二级 Stacking。假设我们有 3 个基模型 M1、M2、M3。
- 基模型 M1,对训练集 train 训练,然后用于预测 train 和 test 的标签列,分别是 \(P_1, T_1\)
对于 M2 和 M3,重复相同的工作,这样也得到 \(P_2, T_2, P_3, T_3\)。
- 分别把 \(P_1, P_2, P_3\) 以及 \(T_1, T_2, T_3\) 合并,得到一个新的训练集和测试集 train2, test2。
- 再用第二层的模型 M4 训练 train2,预测 test2,得到最终的标签列。
Stacking 本质上就是这么直接的思路,但是这样肯定是不行的,问题在于 P1 的得到是有问题的,用整个训练集训练的模型反过来去预测训练集的标签,毫无疑问过拟合是非常非常严重的,因此现在的问题变成了如何在解决过拟合的前提下得到P1、P2、P3,这就变成了熟悉的节奏——K折交叉验证。我们以 2 折交叉验证得到 P1 为例,假设训练集为 4 行 3 列
将其划分为 2 部分
用 traina 训练模型 M1,然后在 trainb 上进行预测得到 pred3 和 pred4
在 trainb 上训练模型 M1,然后在 traina 上进行预测得到 pred1 和 pred2
然后把两个预测集进行拼接
对于测试集 T1 的得到,有两种方法。
注意到刚刚是 2 折交叉验证,M1 相当于训练了 2 次,所以一种方法是每一次训练 M1,可以直接对整个 test 进行预测,这样 2 折交叉验证后测试集相当于预测了 2 次,然后对这两列求平均得到 T1。或者直接对测试集只用 M1 预测一次直接得到 T1。
P1、T1 得到之后,P2、T2、P3、T3 也就是同样的方法。理解了 2 折交叉验证,对于 K 折的情况也就理解也就非常顺利了。所以最终的代码是两层循环,第一层循环控制基模型的数目,每一个基模型要这样去得到 P1,T1,第二层循环控制的是交叉验证的次数 K,对每一个基模型,会训练 K 次最后拼接得到 P1,取平均得到 T1。这下再把@Wille 博文中的那张图片放出来就很容易看懂了。
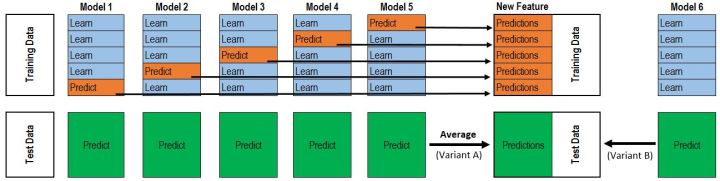
该图是一个基模型得到 P1 和 T1 的过程,采用的是 5 折交叉验证,所以循环了5次,拼接得到 P1,测试集预测了 5 次,取平均得到 T1。而这仅仅只是第二层输入的一列/一个特征,并不是整个训练集。再分析作者的代码也就很清楚了。也就是刚刚提到的两层循环。
python实现
用了一个泰坦尼克号的尝试了一下代码,从头到尾都是可以运行的。代码放在Github,针对其中一段关键的稍作分析
def get_oof(clf, x_train, y_train, x_test):
oof_train = np.zeros((ntrain,))
oof_test = np.zeros((ntest,))
oof_test_skf = np.empty((NFOLDS, ntest)) #NFOLDS行,ntest列的二维array
for i, (train_index, test_index) in enumerate(kf): #循环NFOLDS次
x_tr = x_train[train_index]
y_tr = y_train[train_index]
x_te = x_train[test_index]
clf.fit(x_tr, y_tr)
oof_train[test_index] = clf.predict(x_te)
oof_test_skf[i, :] = clf.predict(x_test) #固定行填充,循环一次,填充一
oof_test[:] = oof_test_skf.mean(axis=0) #axis=0,按列求平均,最后保留一行
return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1) #转置,从一行变为一列
这里只实现了针对一个基模型做 K 折交叉验证,因为 P1 和 T1 都是多行一列的结构,这里是先存储为一行多列,最后进行转置。
但是 Stacking 方法其实在 R 中也有集成好的可以调用。
caretEnsemble包下的caretStack()方法
关键代码如下:
algorithmList <- c('lda', 'rpart', 'glm', 'knn', 'svmRadial')
stackControl <- trainControl(method="repeatedcv", number=10, repeats=3, savePredictions=TRUE, classProbs=TRUE)
stack.glm <- caretStack(models, method="glm", metric="Accuracy", trControl=stackControl)
有一篇博文讲的比较详细
h2o包的h2o.stack()方法
关键代码如下:
nfolds <- 5
glm1 <- h2o.glm(x = x, y = y, family = family,
training_frame = train,
nfolds = nfolds,
fold_assignment = "Modulo",
keep_cross_validation_predictions = TRUE)
gbm1 <- h2o.gbm(x = x, y = y, distribution = "bernoulli",
training_frame = train,
seed = 1,
nfolds = nfolds,
fold_assignment = "Modulo",
keep_cross_validation_predictions = TRUE)
rf1 <- h2o.randomForest(x = x, y = y, # distribution not used for RF
training_frame = train,
seed = 1,
nfolds = nfolds,
fold_assignment = "Modulo",
keep_cross_validation_predictions = TRUE)
dl1 <- h2o.deeplearning(x = x, y = y, distribution = "bernoulli",
training_frame = train,
nfolds = nfolds,
fold_assignment = "Modulo",
keep_cross_validation_predictions = TRUE)
models <- list(glm1, gbm1, rf1, dl1)
metalearner <- "h2o.glm.wrapper"
stack <- h2o.stack(models = models,
response_frame = train[,y],
metalearner = metalearner,
seed = 1,
keep_levelone_data = TRUE)
# Compute test set performance:
perf <- h2o.ensemble_performance(stack, newdata = test)
详情见h2o的Github网站
最后放一张H2O分享的图片总结一下



