对CSS3中的transform：Matrix（）矩阵的一些理解

只要有CSS基础的人肯定都知道，我们可以通过transform中的translate,scale,rotate,skew这些方法来控制元素的平移，缩放，旋转，斜切，其实这些方法呢都是为了便于开发者使用的一个函数；可能大家有时候在用的时候也会有困惑，它们能够改变元素运动，这其中的本质是什么呢？今天我们就来说一说transform: matri()这个东西，如果是2D变换，括号里就是6个值得矩阵，如果是3D变换，括号里就是4*4的16值得矩阵，今天我们就先来看看这个2D变换改变参数达到元素变换的原理。

首先带大家来了解一个概念（实在不喜欢看文字的可以略过这段）

[ 首先我们来说一说何为矩阵，这就要先来扯一扯线性代数的知识了，其实任何一种运动都是在一个特定的空间里进行的，这个空间有它自己特定的运动变换规则，我们的线性空间就属于空间中的一种，线性空间中的运动我们就称之为线性变换，在线性空间里，我们要把一个点运动到任意的另一个点，都可以用线性变换来表示，如何表示呢？当我们在这个线性空间里选择了一个基(所谓基就是能够用来表示空间中所有对象的向量组)，那么我们就可以用向量来描述空间中的任何一个对象，然后用矩阵来描述空间中的变换。而使某个对象发生运动的方法就是用代表运动的矩阵乘以代表对象的那个向量。也就是说，在线性空间选定基之后，++向量刻画对象，矩阵刻画对象的运动，用矩阵与向量的乘法施加运动++。]

• 好了，我们要开始讲重点喽

平移

在CSS3中我们矩阵的原始值是这样的：

transform: matrix(1,0,0,1,0,0);

写成我们数学里矩阵的形式是这样的

这么看起来，我们不太好分辨哪个数字对应的是我们上面写的matrix值里的哪一个，那为了便于描述我们把它写成：

transform: matrix(a,b,c,d,e,f);

那么写成数学矩阵式就是这样的：

根据我们上面说的用矩阵与向量的乘法来施加运动，我们就可以来看一下它到底是怎么运动起来的

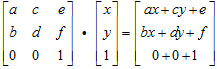
（怎么算的？线性代数忘光光的同学看这里，其实只要把前面横着的a,c,e与后面竖着的x,y,1相乘再相加就ok了）
这么一来我们可以得到一个式子就是：

x'=ax+cy+e
y'=bx+dy+f

x'和y'就是我们变换后的水平位置坐标和垂直位置坐标，现在我们想要把元素往x轴的正方向平移10，在y轴方向上不动,反映到方程式里，我们要怎么来实现呢

元素往x轴的正方形平移10，在y轴方向上不动，反映到方程式里：
x'=ax+cy+e ---（x'=ax+cy+e+10)
y'=bx+dy+f （不变）

元素往y轴的正方向平移10，在x轴方向上不动，反映到方程式里：
x'=ax+cy+e （不变）
y'=bx+dy+f ---（y'=bx+dy+f+10）

元素同时往x轴正向和y轴正向移动10个单位 ：  
我们用css矩阵来写：transform： matrix（1,0,0,1,10,10）--其他数值都不动，e和f分别加10
结论：平移只有跟e和f有关系，跟其他a,b,c,d没有关系，它们该怎么样还是怎么样，e对应x轴的平移，f对应y轴的平移，往正方向平移多少单位就加上多少单位，反之则减去多少个单位。

缩放

平移就是x或者y加减一个常数来得到的，理解了平移之后缩放就很简单了，可不就是x和y的倍数发生了变化么，反映到式子上来那就是系数的变化，那同样道理我们把上面的式子拿过来

x放大2倍 y不变
x'=ax+cy+e---（x'=2ax+cy+e)   就是x的系数增大2倍
y'=bx+dy+f (不变)
y放大2倍 x不变
x'=ax+cy+e (不变)
y'=bx+dy+f---(y'=bx+2dy+f)   就是y的系数增大2倍
x和y都放大2倍，就是x和y的系数都增大2倍
写成矩阵就是：
transform：matrix（2,0,0,2,0,0)
结论：缩放只有跟a和d有关系，跟其他数值都无关，a对应x轴缩放，d对应y轴缩放，缩放多少倍就乘以多少

旋转

相比于平移和缩放，旋转相对来说要复杂点了，当然搞清楚了就没什么难的了
请看

transform：matrix（cosθ，sinθ,-sinθ,cosθ,0,0);

请看实例：

现在我们要让这个元素往顺时针方向旋转45°（sin45°=0.707，cos45°=0.707），那么我们给div加样式如下：

transform: matrix(0.707,0.707,-0.707,0.707,0,0);

看下我们div现在的样子

这个div是不是就按我们预期的一样往顺时针方向转了45°了；

接下来我们把这个旋转放到数学里来看下
那同样的我们把它写成数学里矩阵的形式：

同样的根据矩阵的计算公式，我们可以得到公式：

x'=xcosθ-ysinθ;    
y'=xsinθ+ycosθ

现在我们先把公式放在这里，我们来看一下下图的这个正方形，从图中我们可以知道a,b,c,d的坐标分别为：

A(0,1)   B(1,1)   C(1,0)   D(0,0) 

当我们让它旋转90°之后，那此时的cos45°就是0 sin45°都为1，分别把A,B,C,D里的x,y代入上面的公式之后我们可以得到：

A'(0.707,0.707)   B'(1.414,0)   C'(0.707,-0.707)   D'(0,0) 

现在这个正方形就变成了下图的样子，和我们写代码达到的效果是一样的：

结论：我们要记住初始写法是这样的
transform：matrix（cosθ，sinθ,-sinθ,cosθ,0,0);然后需要旋转多少度就计算出这个度数的cosθ，sinθ就可以达到我们想要的效果啦