神级网络 - UFLDL教程笔记

激活函数：

1）sigmoid函数 - 值域(0,1)

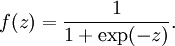
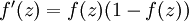
f(z) = \frac{1}{1+\exp(-z)}.   \textstyle f'(z) = f(z) (1-f(z))

2）tanh函数 - 值域(-1,1)

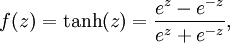
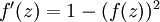
f(z) = \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}},  \textstyle f'(z) = 1- (f(z))^2

两个函数都扩展至向量表示： \textstyle f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]    \textstyle f'([z_1, z_2, z_3]) = [f'(z_1), f'(z_2), f'(z_3)]

 

Network331.png

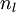\textstyle {n}_l - 网络层数

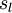\textstyle s_l - 第l层的节点数（不包括偏置单元）

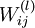\textstyle W^{(l)}_{ij} - 第l层第j单元 与 第l+1层第i单元之间的连接参数，大小为

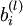\textstyle b^{(l)}_i - 第l+1层第i单元的偏置项 

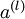\textstyle a^{(l)} - 第l层的激活值 

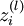\textstyle z^{(l)}_i - 第l层第i单元输入加权和（包括偏置单元）

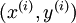\textstyle (x^{(i)}, y^{(i)}) - 样本

m - 样本数

α - 学习率

λ - 权重衰减参数，控制方差代价函数两项的相对重要性。

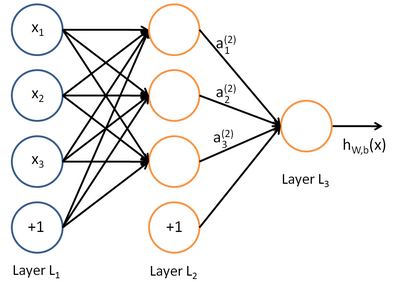
hw,b(x)=a

 

前向传播

初始化 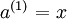\textstyle a^{(1)} = x

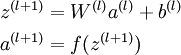\begin{align} z^{(l+1)} &= W^{(l)} a^{(l)} + b^{(l)} \\ a^{(l+1)} &= f(z^{(l+1)}) \end{align} （1）

 

后向传播

===> 目标：整体代价函数最小化 

\begin{align} J(W,b) &= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \\ &= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left\| h_{W,b}(x^{(i)}) - y^{(i)} \right\|^2 \right) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \end{align}  （2）

由单样本代价函数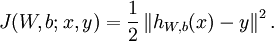 \begin{align} J(W,b; x,y) = \frac{1}{2} \left\| h_{W,b}(x) - y \right\|^2. \end{align}  ， 加上规则化项减少权重幅度，防止过拟合。

 

===> 梯度下降法

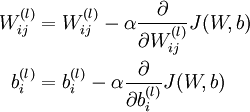\begin{align} W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) \end{align}  （3）

问题转化为求后面两个偏导数

 

===> 整体偏导数转化为单样本偏导数 

\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &= \left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &= \frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \end{align}  （4）

 

===> 后向传播求单样本偏导

先求最后一层

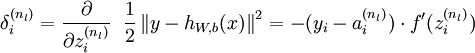
\begin{align} \delta^{(n_l)}_i = \frac{\partial}{\partial z^{(n_l)}_i} \;\; \frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i) \end{align}

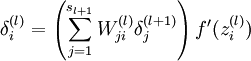
\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)

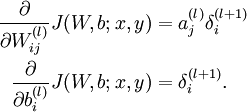\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)}. \end{align}    （5）

 

神经网络伪代码 

当不满足结束条件（迭代次数/结果误差率等）：

　　对所有层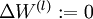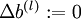，\textstyle \Delta W^{(l)} := 0  \textstyle \Delta b^{(l)} := 00

　　对每个样本(x,y)： 

　　　　#前向传播

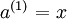
　　　 　\textstyle a^{(1)} = x

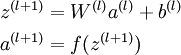
 　　　　 \begin{align} z^{(l+1)} &= W^{(l)} a^{(l)} + b^{(l)} \\ a^{(l+1)} &= f(z^{(l+1)}) \end{align}

　　　　#后向传播

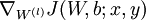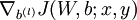
 　　　　利用公式组（5）计算 \textstyle \nabla_{W^{(l)}} J(W,b;x,y)  和 \textstyle \nabla_{b^{(l)}} J(W,b;x,y)

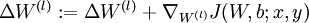
　　　　\textstyle \Delta W^{(l)} := \Delta W^{(l)} + \nabla_{W^{(l)}} J(W,b;x,y)

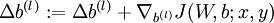
　　　　\textstyle \Delta b^{(l)} := \Delta b^{(l)} + \nabla_{b^{(l)}} J(W,b;x,y)

　　更新权重参数

　　 \begin{align} W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\ b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align}

 

posted on 2016-04-21 22:57  IvanSSSS  阅读(163)  评论(0)  编辑  收藏  举报

导航