潜在语义分析LSA
潜在语义分析通过矢量语义空间来分析文档和词的关系。
基本假设:如果两个词多次出现在同个文档中,则两个词在语义上具有相似性。
LSA使用大量文本构成矩阵,每行表示一个词,一列表示一个文档,矩阵元素可以是词频或TF-IDF,然后使奇异值分解SVD进行矩阵降维,得到原矩阵的近似,此时两个词的相似性可通过其向量cos值。
降维原因:
- 原始矩阵太大,降维后新矩阵是原矩阵的近似。
- 原始矩阵有噪音,降维也是去噪过程。
- 原始矩阵过于稀疏
- 降维可以解决一部分同义词与二义性的问题。
推导:
对于文档集可以表示成矩阵X,行为词,列为文档

词向量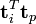 的点乘可以表示这两个单词在文档集合中的相似性。矩阵
的点乘可以表示这两个单词在文档集合中的相似性。矩阵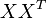 包含所有词向量点乘的结果
包含所有词向量点乘的结果
降维的过程其实是奇异值分解,矩阵X可分解成正交矩阵U、V,和一个对角矩阵 的乘积
的乘积

因此,词与文本的相关性矩阵可表示为:
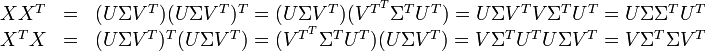
因为![\Sigma \Sigma^T]() 与
与![\Sigma^T \Sigma]() 是对角矩阵,因此
是对角矩阵,因此![U]() 肯定是由
肯定是由![X X^T]() 的特征向量组成的矩阵,同理
的特征向量组成的矩阵,同理![V]() 是
是![X^T X]() 特征向量组成的矩阵。
特征向量组成的矩阵。
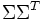 与
与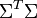 是对角矩阵,因此
是对角矩阵,因此 肯定是由
肯定是由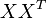 的特征向量组成的矩阵,同理
的特征向量组成的矩阵,同理 是
是 特征向量组成的矩阵。
特征向量组成的矩阵。这些特征向量对应的特征值即为![\Sigma \Sigma^T]() 中的元素。综上所述,这个分解看起来是如下的样子:
中的元素。综上所述,这个分解看起来是如下的样子:
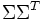 中的元素。综上所述,这个分解看起来是如下的样子:
中的元素。综上所述,这个分解看起来是如下的样子: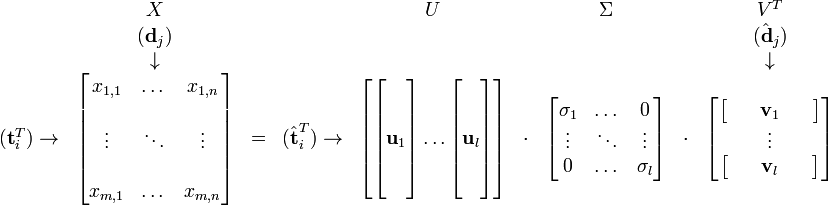
 被称作是奇异值,而
被称作是奇异值,而  和
和 则叫做左奇异向量和右奇异向量。
则叫做左奇异向量和右奇异向量。通过矩阵分解可以看出,原始矩阵中的![\textbf{t}_i]() 只与U矩阵的第i行有关,我们则称第i行为
只与U矩阵的第i行有关,我们则称第i行为 ![\hat{\textrm{t}}_i]() 。
。
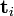 只与U矩阵的第i行有关,我们则称第i行为
只与U矩阵的第i行有关,我们则称第i行为  。
。同理,原始矩阵中的![\hat{ \textrm{d}}_j]() 只与
只与![V^T]() 中的第j列有关,我们称这一列为
中的第j列有关,我们称这一列为![\hat{ \textrm{d}}_j]() 。
。![\textbf{t}_i]() 与
与![\hat{ \textrm{d}}_j]() 并非特征值,但是其由矩阵所有的特征值所决定。
并非特征值,但是其由矩阵所有的特征值所决定。
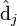 只与
只与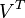 中的第j列有关,我们称这一列为
中的第j列有关,我们称这一列为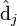 。
。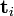 与
与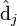 并非特征值,但是其由矩阵所有的特征值所决定。
并非特征值,但是其由矩阵所有的特征值所决定。当我们选择k个最大的奇异值(这里就进行了特征提取),和它们对应的U与V中的向量相乘,则能得到一个X矩阵的k阶近似,此时该矩阵和X矩阵相比有着最小误差(即残差矩阵的Frobenius范数)。
但更有意义的是这么做可以将词向量和文档向量映射到语义空间。向量![\hat{\textbf{t}}_i]() 与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。
与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。
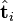 与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。
与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。同理,向量 ![\hat{\textbf{d}}_j]() 也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子:
也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子:
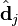 也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子:
也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子: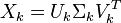
有了这个变换,则可以做以下事情:
- 判断文档
![j]() 与
与 ![q]() 在低维空间的相似度。比较向量
在低维空间的相似度。比较向量 ![\Sigma_k \hat{\textbf{d}}_j]() 与向量
与向量![\Sigma_k \hat{\textbf{d}}_q]() (比如使用余弦夹角)即可得出。
(比如使用余弦夹角)即可得出。 - 通过比较
![\Sigma_k \hat{\textbf{t}}_i^T]() 与
与 ![\Sigma_k \hat{\textbf{t}}_p^T]() 可以判断词
可以判断词![i]() 和词
和词![p]() 的相似度。
的相似度。 - 有了相似度则可以对文本和文档进行聚类。
- 给定一个查询字符串,算其在语义空间内和已有文档的相似性。
要比较查询字符串与已有文档的相似性,需要把文档和查询字符串都映射到语义空间,对于原始文档,由以下公式可以进行映射:

其中对角矩阵![\Sigma_k]() 的逆矩阵可以通过求其中非零元素的倒数来简单的得到。
的逆矩阵可以通过求其中非零元素的倒数来简单的得到。
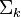 的逆矩阵可以通过求其中非零元素的倒数来简单的得到。
的逆矩阵可以通过求其中非零元素的倒数来简单的得到。同理,对于查询字符串,得到其对应词的向量后,根据公式 ![\hat{\textbf{q}} = \Sigma_k^{-1} U_k^T \textbf{q}]() 将其映射到语义空间,再与文档进行比较。
将其映射到语义空间,再与文档进行比较。
 将其映射到语义空间,再与文档进行比较。
将其映射到语义空间,再与文档进行比较。低维的语义空间可以用于以下几个方面:
- 在低维语义空间可对文档进行比较,进而可用于文档聚类和文档分类。
- 在翻译好的文档上进行训练,可以发现不同语言的相似文档,可用于跨语言检索。
- 发现词与词之间的关系,可用于同义词、歧义词检测。.
- 通过查询映射到语义空间,可进行信息检索。
- 从语义的角度发现词语的相关性,可用于“选择题回答模型”(multi choice qustions answering model)。
LSA的一些缺点如下:
- 新生成的矩阵的解释性比较差.比如
- {(car), (truck), (flower)} ↦ {(1.3452 * car + 0.2828 * truck), (flower)}
- (1.3452 * car + 0.2828 * truck) 可以解释成 "vehicle"。同时,也有如下的变换
- {(car), (bottle), (flower)} ↦ {(1.3452 * car + 0.2828 * bottle), (flower)}
- 造成这种难以解释的结果是因为SVD只是一种数学变换,并无法对应成现实中的概念。
- LSA无法扑捉一词多以的现象。在原始词-向量矩阵中,每个文档的每个词只能有一个含义。比如同一篇文章中的“The Chair of Board"和"the chair maker"的chair会被认为一样。在语义空间中,含有一词多意现象的词其向量会呈现多个语义的平均。相应的,如果有其中一个含义出现的特别频繁,则语义向量会向其倾斜。
- LSA具有词袋模型的缺点,即在一篇文章,或者一个句子中忽略词语的先后顺序。
- LSA的概率模型假设文档和词的分布是服从联合正态分布的,但从观测数据来看是服从泊松分布的。因此LSA算法的一个改进PLSA使用了多项分布,其效果要好于LSA
摘自:http://blog.csdn.net/roger__wong/article/details/41175967
--------------------------------------------------
(* "・∀・)ノ ------◎ 去吧!大师球!!

 与
与  在低维空间的相似度。比较向量
在低维空间的相似度。比较向量 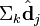 与向量
与向量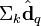 (比如使用余弦夹角)即可得出。
(比如使用余弦夹角)即可得出。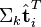 与
与 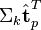 可以判断词
可以判断词 和词
和词 的相似度。
的相似度。 

 浙公网安备 33010602011771号
浙公网安备 33010602011771号