KMP算法的一点学习笔记
博主太菜了,看不懂后缀数组就先滚回来看看KMP。
(假设各位不会什么字符串哈希)
对于子串查找这类问题,如果我单纯询问一个字符串s1中出现了多少次s2,暴力方法很好想,直接固定起点向后枚举,如果在跳到长度为s2之前就出现不同点,那么这个起点就不行,起点向右挪一位,重复这个操作直到跑到(s2-s1+1)的位置。
但这个算法的复杂度非常高,最高可达到O(nm),显然无法解决n>=1000的时候的情况,所以就有了KMP算法。
首先看一看下面这个字符串:
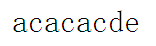
如果我们要在另一个字符串里寻找这个字符串是否出现过,假设我们现在按照暴力的做法去寻找出现了这种情况:

当匹配到acacd的时候,很明显就咕咕了,这个时候按照暴力的思路会直接从cacd....开始找,但如果让我们来进行下一步操作,我们会选择从acdslf.....开始下一次匹配,因为我们很容易发现对于匹配失败前的字符串acac,前缀ac与后缀ac是相同的!所以我们可以直接从第二个a的位置开始下一次匹配,就是这样:

所以根据这个性质,我们可以减少一些无用的移动,从而降低复杂度。
KMP算法步骤如下:
1.定义nxt数组:nxt[i]表示对于匹配字符串的[0~i]位,其相同前缀和后缀的最大长度。还是以上面那张图为例:
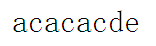
对于这个字符串,nxt数组存储的分别就是"a","ac","aca","acac","acaca","acacac","acacacd","acacacde"的相同前缀和后缀的最大长度,分别就是0(""),0(""),1("a"),2("ac"),3("aca"),4("acac"),0(""),0("")。
所以在匹配的时候,如果在s2第i位匹配失败,那么下一次就可以从当前位置pos+nxt[i]的地方开始匹配。
2.考虑匹配时如何找到当前点对应的最长匹配长度。
如果我们知道了前一个位置的nxt值,那么我们如何得到当前位置的nxt呢?用上面那个例子:

如果我们现在知道了第二个a的最长匹配为3,现在要求第二个c。
发现当前位置与匹配串的3+1位相同,c的最长匹配就为3+1=4。
然后匹配d,发现与4+1位匹配失败,怎么办?
直接跳nxt啦~
为什么呢?
因为acacd和acaca前四位是相同的,所以既然四位不行,那么就看最长相同前缀和后缀可不可以啦~
但是发现ac(acd)和(aca)ca并不匹配(看括号内的部分)。
所以再跳nxt!
然后就跳到0了。。。而且跳到0后d和a也不匹配,所以d这个位置最长匹配长度为0。
以此类推即可!
所以匹配部分就完了!
3.那么问题来了,如何去求nxt数组呢?
还是利用类似的思想,如果我们知道了i-1的nxt值,我们如何求i的nxt值呢?
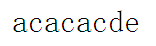
首先,当前位置最佳情况的nxt值就是nxt[i-1]+1,所以先copy下nxt[i-1]。
如上,如果我们已经求得acaca的nxt为3,如何求acacac呢?
发现当前位置=s[nxt[i-1]+1],所以当前位置的nxt直接求得为nxt[i-1]+1。
然后求acacacd的nxt。
发现d与s[nxt[i-1]+1]=a不相等,所以跳nxt[i-1]的nxt。
相信很多人会一脸懵逼,为什么?(反正之前我是打死没看懂然后突然天空一声巨响思路一下豁然贯通)
首先再看一下nxt数组的定义:最长相同前缀和后缀的长度。所以我们要在当前位置前加上那么一段长度为x的字符,使s[1~x+1](当然会因为题目实际情况改一下下标,这里为了方便就用1作为起始下标)与这段字符相同,当然我们希望越长越好,所以我们会从前一位的nxt再跳nxt,因为加的一段字符既是前面字符串的前缀也为其后缀,所以最大的即为前一位的nxt,第二小的即为前一位的nxt的nxt啦,这样一直判一直判就可以得到最大的长度了。
好吧可能写的有点模糊如果不懂欢迎提问,我会解答!
然后贴代码,例题洛谷模板
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
char s1[MAXN],s2[MAXN];
int len1,len2;
int tot;
int nxt[MAXN];
void calc_nxt(){
nxt[0]=-1;
int k=-1;
for(int q=1;q<len2;++q){
while(k>-1&&s2[k+1]!=s2[q]){
k=nxt[k];
}
if(s2[k+1]==s2[q])
k++;
nxt[q]=k;
}
}
void kmp(){
int k=-1;
for(int i=0;i<len1;++i){
while(k>-1&&s2[k+1]!=s1[i])
k=nxt[k];
if(s2[k+1]==s1[i])
k++;
if(k==len2-1)
cout<<i-len2+2<<'\n';
}
}
int main(){
scanf("%s",s1);
len1=strlen(s1);
scanf("%s",s2);
len2=strlen(s2);
calc_nxt();
kmp();
for(int i=0;i<len2;++i)
cout<<nxt[i]+1<<' ';
return 0;
}


