洛谷1361 小M的作物（最小割）

传送门

【题目分析】

第一眼看有A,B两个以为是二分图，根据题目各种想办法建边，感觉还是弄不成。

推了好久才发现求的就是一个最小割。

首先如果令m=0，那么可以建这样一个图：

当然贪心就可以了，最后选择的方案也一定是取ai和bi中的较大值，算出来也正是这张图的最小割，也是最大流。

那如果m不为0呢？

我们举一个有两个点的例子：

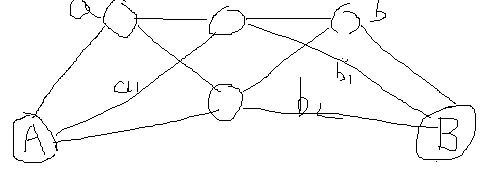
a表示全部选种A地，b表示全部选种B地。

将a，b到两个点的容量设为INF，所以做最小割的时候一定不会去割INF的边，所以这个图的最小割就是这两种作物不选用的最小值，用总值减去即可得到最大贡献。

所以以此类推即可。

所以就是一道最小割嘛。

【代码~】

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2010;
const int MAXM=1e6+10;
const int INF=0x3f3f3f3f;

int n,m,cnt,s,t,sum;
int head[MAXN],depth[MAXN],cur[MAXN];
int nxt[MAXM],to[MAXM],w[MAXM];
int a[MAXN],b[MAXN];

int Read(){
	int i=0,f=1;
	char c;
	for(c=getchar();(c>'9'||c<'0')&&c!='-';c=getchar());
	if(c=='-')
	  f=-1,c=getchar();
	for(;c>='0'&&c<='9';c=getchar())
	  i=(i<<3)+(i<<1)+c-'0';
	return i*f;
}

void Add(int x,int y,int z){
	nxt[cnt]=head[x];
	head[x]=cnt;
	to[cnt]=y;
	w[cnt]=z;
	cnt++;
}

void add(int x,int y,int z){
	Add(x,y,z);
	Add(y,x,0);
}

int bfs(){
	memset(depth,0,sizeof(depth));
	depth[s]=1;
	queue<int> q;
	q.push(s);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=-1;i=nxt[i]){
			int v=to[i];
			if(!depth[v]&&w[i]){
				depth[v]=depth[u]+1;
				q.push(v);
				if(v==t)
				  return 1;
			}
		}
	}
	return 0;
}

int dfs(int u,int flow){
	if(u==t)
	  return flow;
	for(int &i=cur[u];i!=-1;i=nxt[i]){
		int v=to[i];
		if(depth[v]==depth[u]+1&&w[i]){
			int di=dfs(v,min(w[i],flow));
			if(di){
				w[i]-=di;
				w[i^1]+=di;
				return di;
			}
		}
	}
	return 0;
}

int dinic(){
	int ans=0;
	while(bfs()){
		for(int i=s;i<=t;++i)
		  cur[i]=head[i];
		while(int d=dfs(s,INF))
		  ans+=d;
	}
	return ans;
}

int main(){
	memset(head,-1,sizeof(head));
	n=Read();
	for(int i=1;i<=n;++i){
		a[i]=Read();
		sum+=a[i];
	}
	for(int i=1;i<=n;++i){
		b[i]=Read();
		sum+=b[i];
	}
	m=Read();
	s=0,t=n+m+m+1;
	for(int i=1;i<=n;++i){
		add(s,i,a[i]);
		add(i,t,b[i]);
	}
	for(int i=1;i<=m;++i){
		int k=Read();
		int c1=Read(),c2=Read();
		sum+=c1+c2;
		add(s,i+n,c1);
		add(i+n+m,t,c2);
		for(int j=1;j<=k;++j){
			int x=Read();
			add(i+n,x,INF);
			add(x,i+n+m,INF);
		}
	}
	cout<<sum-dinic();
	return 0;
}