Trie树一点学习笔记

写在前面

蒟蒻太菜了看不懂AC自动机指针版（其实就是不会指针），所以反过头来重新看看Trie树。

Trie树是什么？

Trie树，又称字典树，其实为前缀树，因为从根节点到每一个节点都会对应原众多字符串的其中一些的前缀。Trie树上可以打标记，含义随题意而变。

Trie树也是某种意义上的自动机，节点代表状态，边代表转移。

举个小例子：

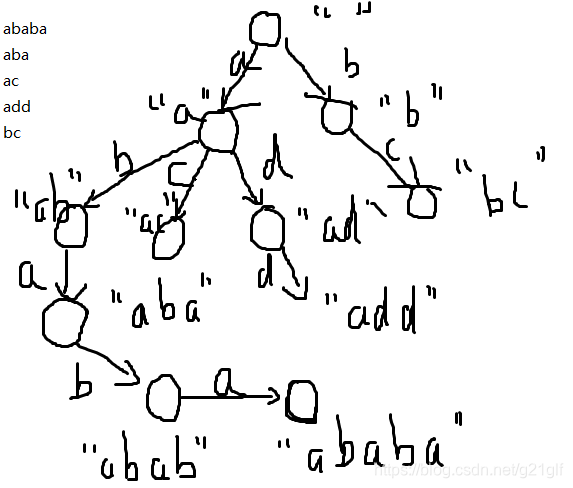
（woc画丑了）

Trie树的一些操作

1.插入

因为建树过程其实就是将字符串插入，那么建树就与插入操作一样。

考虑已经插入了n-1个字符，接下来插入第n个字符，可以发现，如果当前状态有转移到现在这个字符串的转移，那么可以直接跳到该状态，处理下一个字符。

如果没有的话就从当前状态新建一个转移指向这个状态就行了。

代码看看下面例题。

2.查询

与插入操作类似，沿着树往下跳即可，直到跳完或者没有转移。

一些小应用

其实纯Trie树思维含量不高，纯背板子都可以，一般只会在打标记上稍作修改。

查询互为前缀的数量

统计节点数

讲讲代码

以秘密消息一题为例

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
const int LEN=1e4+10;

int n,q;
int siz,k,a[LEN];
struct Trie{                //用结构体封装一下（数组也可以）
	int pass,end;
	int son[2];
}tr[MAXN];

int Read(){
	int i=0,f=1;
	char c;
	for(c=getchar();(c>'9'||c<'0')&&c!='-';c=getchar());
	if(c=='-')
	  f=-1,c=getchar();
	for(;c>='0'&&c<='9';c=getchar())
	  i=(i<<3)+(i<<1)+c-'0';
	return i*f;
}

void insert(){
	for(int i=1;i<=k;++i){
		a[i]=Read();
	}
	int last=0;
	for(int i=1;i<=k;++i){
		tr[last].pass++;
		if(!tr[last].son[a[i]]){  //如果没有这个儿子就新建一个节点，siz表示当前节点编号
			tr[last].son[a[i]]=++siz;
			memset(tr[siz].son,0,sizeof(tr[siz].son));//防止随机数
		}
		last=tr[last].son[a[i]];
	}
	tr[last].end++; 
}

int query(){      //查询操作与插入操作无太大差别
	int ret=0;
	for(int i=1;i<=k;++i){
		a[i]=Read();
	}
	int last=0;
	for(int i=1;i<=k;++i){
		ret+=tr[last].end;
		if(!tr[last].son[a[i]]){   //没有转移直接退出
			return ret;
		}
		last=tr[last].son[a[i]];   //否则跳到下一个状态
	}
	ret+=tr[last].pass+tr[last].end;
	return ret;
}

int main(){
	n=Read(),q=Read();
	for(int i=1;i<=n;++i){
		k=Read();
		insert();
	}
	for(int i=1;i<=q;++i){
		k=Read();
		cout<<query()<<'\n';
	}
	return 0;
}

小结一下，Trie树的思想还是很好懂的，当然如果静态数组炸空间了的话，如果复杂度可以接受可以将数组用map来代替，从而达到节省空间的目的。

一些比较毒瘤的Trie树上的题：

SCOI2016背单词（纯在Trie上xjb搞）

ZJOI2015诸神眷顾的幻想乡（Trie树上建SAM，其实就是SAM写的时候多一排（bfs写法）但我真的不会qwq）

Thanks for reading