POJ3907 Build Your Home(向量基本运算求多边形面积)
古伽兰那
【题目大意】
给你一个多边形,询问其面积。
【输入格式】
输入包含多组数据,每组数据第一个数为N,表示为N边形,接下来给出N对(x,y),表示多边形顶点的坐标(x,y为实数,顶点按顺时针或逆时针给出)
【输出格式】
对于每组数据输出多边形面积(四舍五入)。
【样例输入】
1 123.45 67.890
3 0.001 0 1.999 0 0 2
5 10 10 10 12 11 11 12 12 12.0 10.0
0
【样例输出】
0
2
3
【题目分析】
求多边形面积。。。。。好板啊。。。。。。
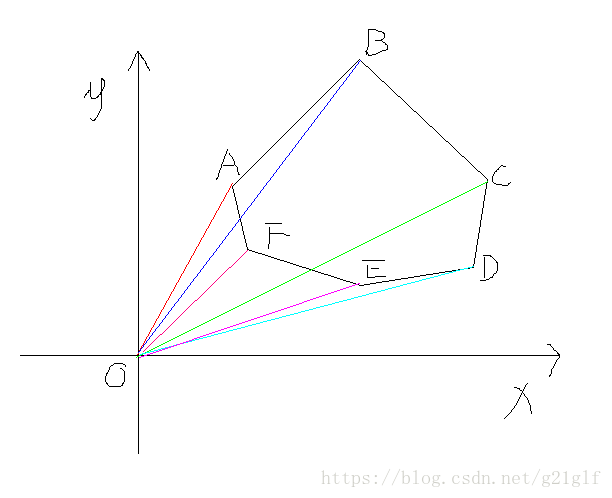
对于一个多边形的面积就视作多个三角形的面积求和(当然是方向面积),如下图所示:
因为我们计算的是有向面积,根据给出顶点的顺序,有可能会出现最后算出的面积为负的情况,所以我们还要取个绝对值。
最后提醒一点:叉积得到的是平行四边形的面积,所以要除以2!除以2!
【代码~】
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN=1e5+10;
int n,m;
struct point{
double x,y;
point(double a=0,double b=0){
x=a,y=b;
}
friend inline point operator+(const point &a,const point &b){
return point(a.x+b.x,a.y+b.y);
}
friend inline point operator-(const point &a,const point &b){
return point(a.x-b.x,a.y-b.y);
}
friend inline double operator*(const point &a,const point &b){
return a.x*b.y-a.y*b.x;
}
friend inline double dot(const point &a,const point &b){
return a.x*b.x+a.y*b.y;
}
inline double dist()
{
return x*x+y*y;
}
};
struct polygon{
point q[MAXN];
}a;
double area()
{
if(n==1||n==2)
return 0;
double ret=0;
a.q[n+1]=a.q[1];
for(int i=1;i<=n;++i)
ret+=a.q[i]*a.q[i+1];
return ret/2;
}
int main()
{
while(scanf("%d",&n)&&n)
{
for(int i=1;i<=n;++i)
scanf("%lf%lf",&a.q[i].x,&a.q[i].y);
cout<<(int)(fabs(area())+0.5)<<'\n';
}
return 0;
}