每日一题
CF1553E 2100* Permutation Shift
那时的我不会,还记得这题前一天晚上丢给 lyx 和 5k,然后他俩晚休前就秒了,到第二天中午没睡觉,在办公室玩这个,也没玩明白,下午看题解才发现有一个重要性质根本没用,然后就改出来了,那段时间也挺有意思的。
给了一个 \(m\le \frac{n}{3}\),不觉得很神秘吗,来研究一下这里,首先有经典东西:每次交换最多可以改变两个数的位置。也就是说,有至多 \(2m\) 的数匹配不上移位,剩下至少 \(\frac{n}{3}\) 个数一定可以与移位匹配上,考虑找出这样的匹配位置来。
对于每一个位置都求出他需要的 \(k\),只有个数大于等于 \(\frac{n}{3}\) 的 \(k\) 值才有可能是答案,换句话说,合法的 \(k\) 最多有 \(3\) 个,枚举并直接暴力检查交换次数是否不超过 \(m\) 就行了。
当然,最后的检验也可以不那么简单粗暴,一个排列到另一个排列的最小交换次数就等于 \(n\) 减去相应位置连边后的图的环数。证明就是最后一定全是自环,而每次交换可以把一个环变成两个,增加了一个环。
CF1463D 1900* Pairs
这是啥,太简单了所以一点印象都没有,两三眼瞪出来合法的 \(x\) 是连续的一段,所以找答案极值即可,直接考虑最多取小数和最多取大数即可。
CF1665D 1900* GCD Guess
交互的起点,这题有印象,晚上睡觉时想出来的,现在其实看到 \(30\) 次就一眼了吧。记得第二天还跟李凯安他们玩这个东西。
首先能想到先判奇偶,发现只要给一个 \((1,3)\) 观察 gcd 是否为 \(1\) 就行了,为啥能这么干,因为我们知道这一位后面没有别的数,所以这一位上操作不会有更低的位来影响,现在考虑依次确定 \(x\) 的每一个二进制位,每次考虑将后面的影响消除,设已经得到的答案为 \(ans\),对于从右往左第 \(k\) 位,问 \((2^k-ans,2^{k+1}+2^k-ans)\),这样首先会给这一位加上 \(1\),如果这一位本来是 \(0\),一定会返回 \(2^k\),否则返回更大的数。
CF1762D 2100* GCD Queries
这个真是牛逼题,当时三个人都不会,5k 还想上随机化,看题解发现有高水平选手不会,看完之后感觉确实很牛逼。然后第二天又跟李凯安玩这个。
首先 \(0\) 和 \(x\) 的 \(\gcd\) 为 \(x\),也就是说 \(0\) 可以肆意做到和一个数的 \(\gcd\) 最大,考虑排除不可能的情况,比如现在问了 \((a,b),(b,c)\) 如果 \(\gcd(a,b)=\gcd(b,c)\) 那么 \(b\not=0\),如果 \(\gcd(a,b)<\gcd(b,c)\) 那么 \(a\not=0\),反之 \(c\not=0\),那么每两次询问就可以排除一个位置,最后会剩下两个数,这时什么都不能确定,给出两个位置就行。
CF1634D 2000* Finding Zero
忘了是啥课了,教室里没人,跟 lyx 在教室没出去,然后跟上一个是一个 trick,所以想的都很快。
怎么感觉现在不是很会了,跟 CF1762D 差不多是一个套路,下文中 \((a,b,c)\) 表示询问 \(a,b,c\) 三个位置的结果,\(x\) 位置的值记作 \(x\)。
还是考虑排除不合法情况,如果三个数中有 \(0\) 那么返回的数一定最大,考虑四个位置 \(a,b,c,d\),钦定一下 \(a\le b\le c\le d\),\((a,b,c)=c-a,(a,b,d)=d-a,(a,c,d)=d-a,(b,c,d)=d-b\),发现有两个 \(d-a\) 且 \(d-a\ge c-a,d-a\ge d-b\),所以一定有两个询问结果相等,且他们是最大值。
如果有两个结果相等,那么 \(a<b<c<d\),可以找到相应的两个询问,这两个询问不共有的两个位置一定对应着 \(b,c\),可以直接排除。如果三个相等,那么 \(a<b<c=d\) 或者 \(a=b<c<d\),剩下的一个询问中的位置对应着 \(b,c,d\),直接排除。如果四个相等,那么 \(a=b=c=d\),全部都排除掉。经过上述分析,每四次询问可以至少排除两个位置,最后剩下两个,保证了询问次数。
CF1103B 2000* Game with modulo
我去,居然现在没有一眼会。
根据范围的提示,猜想是二分或者二进制相关,但是发现这个东西的函数图像是一段一段的,不能二分。
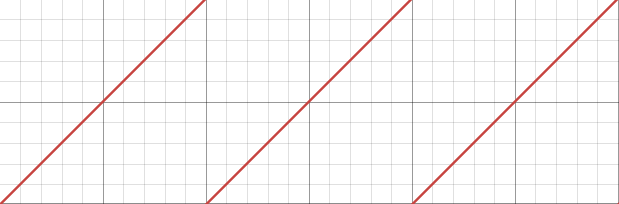
但是如果能找到确定相邻的两段图像,就可以二分出来两端函数图像的交界处,也就是答案的倍数,如果是第一段和第二段图像,那么二分出来的就是确切的答案,考虑如何找到这两个相邻的图像。
观察发现,随着我们询问的数越来越大,结果也越来越大,达到 \(a\) 之后就会骤降,考虑找出这样的骤降点。
第一次询问 \((0,1)\),如果返回 x 那么 \(a=1\),再询问 \((1,2)\),如果答案返回 x 那么 \(a\le 2\),再询问 \((2,4)\) 如果返回 x,那么 \(a\le 4\),再询问 \((4,8)\),如果返回 x,那么 \(a\le 8\),以此类推,考虑每次倍增询问,这样第一个返回 \(x\) 的询问 \((x,2x)\) 就会确定 \(x\le a\le 2x\),且他们都在函数的第一段图像上,所以二分出来的就是答案。
简单说下为什么这样在第一段图像上,因为每次 \(y=2x\),所以不会再次跨越一段函数图像。
时间过得真快,有生之年这个博竟然又更新了,怎么上面都不写下解题过程。
CF1842D 1900* Tenzing and His Animal Friends
这个是 CTH 在万豪附中给我随出来的,发现有诸多限制,直接连边,然后简单手玩发现答案就是 \(1\) 到 \(n\) 的最短路,输出方案有点逆天,不过直接考虑每条边的剩余代价,依次扩展到 \(n\) 即可。
CF1976C 1600* Job Interview
为啥要写这个,因为那一场 CF 是放假期间,lyx 打了,我看了一眼 C,然后 vx 给他口胡了一下,当时脑子不清楚感觉也不太明白,所以现在随便写了写,首先处理前 \(n\) 个的答案,然后分讨找出出第一个冲突位置,计算新贡献即可,冲突位置固定,所以直接线性就行。
CF1856D 2100* More Wrong
还是交互题有意思,套路交互都比传统题有意思。其实是找最大值,开始想的是倒着扫,实时维护当前最大值,然后往前找第一个比它大的值,但是这个二分找的过程代价有点爆炸,如果他是递减的就炸完了,那我们修补一下,从前面也扫最大值,两个指针对着扫,每个指针处理一半,然后合并,但是这样如果是个单峰的话代价还是很大,发现这样做就将原问题分成了两个子问题,不妨继续划分,类似于归并排序的思想,每次把一个区间划分成两个处理最大值位置,然后合并,代价形如 \(T(n)=2T(\frac{n}{2})+n^2\),根据主定理得出代价在 \(n^2\) 级别,不太会主定理,但是我们可以直接类似线段树分析,贡献乘 \(2\),然后合并有一个 \(2\) 的常数,所以理论总代价在 \(4n^2\) 以内,感觉一路想过来很自然。
CF1153E 2200* Serval and Snake
qnmd,困死我了,天天没精神,I need a vacation !
感觉比较平凡,不知道为啥有紫,zby 两眼秒了。
只有端点的度为 \(1\),所以如果一个询问结果是奇数,端点一定在这个范围内,不难想到对于所有行问一次,对于所有列问一次,接下来有两种情况。
- 端点在不同行,不同列,这时直接问一个点是否是端点就能确定位置了。
- 端点在同行或同列,只说下同行,这时已经确定了端点所在的两列,只考虑一列,在这一列上二分询问,端点在结果是奇数的一部分,然后就可以找到端点所在行数,同列同理。
总次数不会超过 \(2009\),感觉答案范围的提示性也很强。
不太想开交互了,天天模拟赛不会,最近应该会开些不是交互的有趣题。
我说怎么就这么点,原来有几道放在别的地方了,搬一下。
CF1808D Petya, Petya, Petr, and Palindromes
比较水的题。首先直接不太好想,正难则反,考虑将所有不需要改变的点对处理出来,拿总数一减就是答案。
发现合法数就是两个位置的数相同,所以就变成了,对于每一个数,查询指定区间内与它相等的数的个数。
因为需要满足回文的对称性,所以偶数位置只会和偶数位置匹配,奇数位置只会和奇数位置匹配,此时其实可以直接无脑上数据结构了,时间复杂度 \(\mathcal{O}(n\log n)\)。
不考虑数据结构,这里有两种处理方法。
- 开个桶记录一下每个数的出现次数,类似莫队的思想,两个指针记录一下桶的范围,每次查到 \(a_i\) 时,求出与 \(a_i\) 的对应位置范围,然后移动指针,如果位置 \(j\) 与 \(i\) 奇偶性相同,就产生 \(1\) 的贡献,奇数偶数各查一次。
- 开桶记录每个数出现的奇数位置和偶数位置,对于每个数,双指针不断向右扩展,直到不合法时记录一下两个指针之间的数的个数,也是奇数偶数都查一次。
这两种做法的时间复杂度都是 \(\mathcal{O}(n)\),做法一因为区间单调,所以保证了复杂度,做法二显然是线性,这里给出做法一的代码。
CF1526D Kill Anton
感觉是比较神的构造,直接构造答案,比较困难,思考 \(b\) 串到 \(a\) 的最大代价,因为交换相邻的元素,可以想到逆序对,给序列 \(a\) 依次标号,这样由 \(b\) 到 \(a\) 的交换次数就是 \(b\) 的逆序对数量。题目就转化为了求逆序对数量最多的 \(b\) 串,但是同种字母之间是没有区别的,所以在最优策略下,同种字母直接是不会进行交换的,不属于逆序对,所以不能简单的将 \(a\) 串翻转。
有引理:一定存在所有同类字母相邻的最优答案。
感性理解:因为字母之间只会不同类交换,所以考虑把不同类的字母尽量放前面,同类在一起。
证明:
- 在最优策略下,同类字母不会发生交换,所以对于任意排列,同类字母之间的标号都是递增的。
- 对于同类字母 \(a_i\) 与 \(a_j\) 之间的所有相邻异类字母 \(a_k\) 到 \(a_q\) 来说,如果 \(a_k\) 这种字母中 \(w\) 个字母与前面的 \(a_i\) 这种字母共构成了 \(v_1\) 个逆序对,\(s\) 个与后面的 \(a_i\) 这种字母共构成了 \(v_2\) 个逆序对,有 \(v_1\le (k-i)\times w,v_2\le (j-q)\times s\)。如果将所有的 \(a_k\) 交换到前面,此时新增了 \([(k-i)\times s-v_1]\) 个逆序对,如果将他们交换到后面,此时新增了 \([(j-q)\times w-v_2]\) 个逆序对。
- 当 \((k-i)\times s-v_1\le 0\),即 \((k-i)\times s\le (k-i)\times w\) 时,有 \(s\le w\),则 \(v_2\le(j-q)\times s\le(j-q)\times w\),即 \((j-q)\times w-v_2\ge 0\)。同理,如果 \((j-q)\times w-v_2\le 0\),则 \((k-i)\times s-v_1\ge 0\)。
- 所以对于任何一种情况,我们总能使得同类字母相邻且逆序对数量单调不减,即一定存在所有同类字母相邻的最优答案。
由于不确定字母之间的顺序,我们可以直接枚举排列,然后每次用树状数组查询逆序对数量(当然也可以 \(\mathcal{O}(n)\) 直接计算交换次数),取最大即可,时间复杂度 \(\mathcal{O}(24n\log n)\)。
CF1736D Equal Binary Subsequences
感觉是对脑电波题,能对上黄,对不上紫。
首先对于 \(1\) 和 \(0\) 的个数是奇数的话一定不合法,特判掉即可。
经过一些数据的模拟,我们好像并不能找出完全不合法的情况,这时可以大胆猜测如果数量不是奇数的话一定有解。
考虑什么样的序列一定是合法的,不难发现,两位两位的进行分组,每组都一样的序列一定是合法的,如 1111001100 或 0000111100,对于答案 \(p\),直接选奇数位就可以。
事实上,对于任意一个可能合法的序列,都能构造出一种方案,使得他与上面序列同构。
具体来说,我们扫描每一组,如果这两个数不一样,选出一个和上一个选择不一样的那一位(如果上次没选过就随便选),扫描完毕后,将选出的子序列右移一位。此时每组的两个数都相同,合法。
考虑为什么第一组的数也一定相同:因为 \(1\) 和 \(0\) 的个数为偶数,所以选出来的数一定有偶数个 \(0\) 和 \(1\),并且他们是交错的,所以右移之后一定能使每一组的数都相同。
我草,好像这里面还真有比较牛的题。



