Kruskal 重构树学习笔记

1.Kruskal 重构树学习笔记2024-07-26

2.珂朵莉树（ODT）学习笔记2024-10-07

Kruskal 想必大家都不陌生，这是一种求最小生成树的算法。
关于 Kruskal 重构树，就是把一张图转化为一个堆。
具体来说，我们可以处理出来从 $u$ 到 $v$ 路径中的点权或边权的极值。

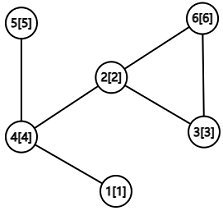
比如上面这张图（前为编号，[ ]内为点权），我们可以将它重构为小顶堆，如下

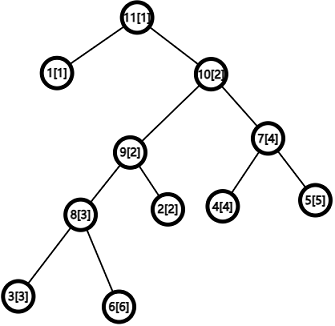
请注意，这棵树有着严格的方向，节点11为他的根节点。
那么如何去实现这个过程呢。
我们仍然是将边排序，然后扫描，用并查集判断是否合法，和正常的 $K r u s k a l$ 最小生成树算法一样。
如果当前边 $(u, v)$ 合法，我们需要找到 $u$ 的父亲 $f u$ 和 $v$ 的父亲 $f v$ ，然后新建一个节点 $t o t$ 点权为 $w_{t} o t = m i n (w_{f} u, w_{f} v)$ 。新建两条边 $t o t \to f u$ 和 $t o t \to f v$ ，当合法的边数达到 $2 \cdot n - 2$ 条时，算法结束。
显然最后会构成一颗二叉树，且满足 $w_{i} \leq w_{x} (i \in s i z_{x})$ 。这棵树的所有叶子结点都是真实点，且任意两点之间路径上的最小节点权值为这两个点的 $l c a$ 的权值。
那么 $K r u s k a l$ 重构树能够解决什么样的问题呢？
P1967 [NOIP2013 提高组] 货车运输
这道题要求两点之间路线中边权的最小值最大，我们可以重构出一个小顶堆，然后查询 $u$ 和 $v$ 的 $l c a$ 的权值是否合法即可。
求 $l c a$ 直接倍增即可。
代码如下

 #include<bits/stdc++.h>
#define endl '\n'
inline int read(){
    char ch=getchar();int x=0,f=1;
    for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
    for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
    return x*f;
}
const int N=1e5+10;
int n,m,q,fa[N],st[20][N],head[N],cnt,dfn_cnt,dfn[N],f[N],dep[N],w[N];
bool vis[N];
struct EDGE{int u,v,w;}ed[N];
struct edge{int v,nex;}e[N<<1];
inline void add(int u,int v){e[++cnt]={v,head[u]},head[u]=cnt;}
inline bool cmp(EDGE a,EDGE b){return a.w>b.w;}
inline int get(int x,int y){return dep[x]<dep[y]?x:y;}
inline void dfs(int x,int fa){
    vis[x]=1;
    st[0][dfn[x]=++dfn_cnt]=x;f[x]=fa;dep[x]=dep[fa]+1;
    for(int i=head[x];i;i=e[i].nex)dfs(e[i].v,x);
}
inline int LCA(int u,int v){
    if(u==v)return u;
    if((u=dfn[u])>(v=dfn[v]))std::swap(u,v);
    int d=std::__lg(v-u++);   
    return f[get(st[d][u],st[d][v-(1<<d)+1])];
}
inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void Kruskal(){
    for(int i=1;i<=2*n;++i)fa[i]=i;
    std::stable_sort(ed+1,ed+m+1,cmp);
    int _new=n;
    for(int i=1;i<=m&&cnt<=2*n-2;++i){
        int u=find(ed[i].u),v=find(ed[i].v);
        if(u==v)continue;
        ++_new;add(_new,u),add(_new,v);
        fa[u]=fa[v]=_new;
        w[_new]=ed[i].w;
    }
    for(int i=_new;i;--i)
        if(!vis[i])dfs(i,0);
    n*=2;
    for(int i=1;i<=std::__lg(n);++i)
        for(int j=1;j+(1<<i)-1<=n;++j)
            st[i][j]=get(st[i-1][j],st[i-1][j+(1<<i-1)]);
}
inline void work(int u,int v){
    if(find(u)!=find(v)){std::cout<<-1<<'\n';return;}
    std::cout<<w[LCA(u,v)]<<'\n';
}
int main(){
    // freopen("in.in","r",stdin),freopen("out.out","w",stdout);
    std::ios::sync_with_stdio(false);
    std::cin.tie(0),std::cout.tie(0);
    n=read(),m=read();
    for(int i=1;i<=m;++i)ed[i].u=read(),ed[i].v=read(),ed[i].w=read();
    Kruskal();
    q=read();
    for(int i=1,u,v;i<=q;++i)u=read(),v=read(),work(u,v);
}

其中 Kruskal 重构树(板子)的部分是

 inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void Kruskal(){
    for(int i=1;i<=2*n;++i)fa[i]=i;
    std::stable_sort(ed+1,ed+m+1,cmp);
    int _new=n;
    for(int i=1;i<=m&&cnt<=2*n-2;++i){
        int u=find(ed[i].u),v=find(ed[i].v);
        if(u==v)continue;
        ++_new;add(_new,u),add(_new,v);
        fa[u]=fa[v]=_new;
        w[_new]=ed[i].w;
    }
    for(int i=_new;i;--i)
        if(!vis[i])dfs(i,0);
    n*=2;
    for(int i=1;i<=std::__lg(n);++i)
        for(int j=1;j+(1<<i)-1<=n;++j)
            st[i][j]=get(st[i-1][j],st[i-1][j+(1<<i-1)]);
}

这是另一道题 P4899 [IOI2018] werewolf 狼人
思路：从起点找到所有可以到达的点权大于等于 $L$ 的节点，为集合 $A$ ，然后从终点找到所有可以到达的点权小于等于 $R$ 的点，为集合 $B$ 。如果 $A ⋂ B \neq \emptyset$ ，则存在这样的路径，否则不存在。
考虑 kruskal 重构树，构建一个小顶堆（人走），然后从起点往上跳到最后一个权值大于等于 $L$ 的节点，此时这个点的子树中就全是权值小于等于 $L$ 的点。大顶堆（furry走）同理。
两个堆分别建一个 dfn 序列 $a$ 和 $b$ ，此时就相当于询问序列 $a$ 中 $l_{a}$ 到 $r_{a}$ 范围内的元素有没有在序列 $b$ 中 $l_{b}$ 到 $r_{b}$ 的范围内出现。（二维数点），直接上离线树状数组或者主席树即可。

 #include<bits/stdc++.h>
inline int read(){
	char ch=getchar();int x=0,f=1;
	for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
	for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
	return x*f;
}
const int N=4e5+10;
int n,m,q;
struct Edge{int u,v,w;}ed[N];
inline bool cmp_per(Edge a,Edge b){return a.w>b.w;}
inline bool cmp_wolf(Edge a,Edge b){return a.w<b.w;}
struct Ktree{
	int dfn[N],fa[N],st[25][N],head[N],val[N],dfn_cnt=0,e_cnt=0,lf[N],rf[N];
	struct edge{int v,nex;}e[N];
	inline void add(int u,int v){e[++e_cnt]={v,head[u]};head[u]=e_cnt;}
	inline int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
	inline void dfs(int x){
		lf[x]=++dfn_cnt;dfn[dfn_cnt]=x;
		for(int i=1;i<=20;++i)st[i][x]=st[i-1][st[i-1][x]];
		for(int i=head[x];i;i=e[i].nex)dfs(e[i].v);
		rf[x]=dfn_cnt;
	}
	inline void build(int type){
		for(int i=1;i<=2*n-1;++i)fa[i]=i;
		for(int i=1;i<=m;++i)ed[i].w=type?std::min(ed[i].u,ed[i].v):std::max(ed[i].u,ed[i].v);
		if(type)std::stable_sort(ed+1,ed+m+1,cmp_per);else std::stable_sort(ed+1,ed+m+1,cmp_wolf);
		int node_tot=n+1;
		for(int i=1;i<=m&&node_tot<=2*n-1;++i){
			int u=ed[i].u,v=ed[i].v,w=ed[i].w;
			int fu=find(u),fv=find(v);
			if(fu!=fv){
				val[node_tot]=w;
				add(node_tot,fu),add(node_tot,fv);
				st[0][fu]=st[0][fv]=fa[fu]=fa[fv]=node_tot;
				node_tot++;
			}
		}
		dfs(node_tot-1);
	}
	inline int get(int x,int v,int type){
		for(int i=20;i>=0;--i){
			if(type&&st[i][x]&&val[st[i][x]]>=v)x=st[i][x];
			if(!type&&st[i][x]&&val[st[i][x]]<=v)x=st[i][x];
		}
		return x;
	}
}Per,Wolf;
int root[N],cnt;
struct Tree{int siz,ls,rs;}t[N<<5];
inline void update(int p){t[p].siz=t[t[p].ls].siz+t[t[p].rs].siz;}
inline void insert(int last,int p,int x,int l,int r){
	if(l==r){t[p].siz=t[last].siz+1;return;}
	int mid=(l+r)>>1;t[p]=t[last];
	if(x<=mid)insert(t[last].ls,t[p].ls=++cnt,x,l,mid);
	else insert(t[last].rs,t[p].rs=++cnt,x,mid+1,r);
	update(p);
}
inline int query(int last,int p,int x,int y,int l,int r){
	if(l>=x&&r<=y){return t[p].siz-t[last].siz;}
	int mid=(l+r)>>1,ans=0;
	if(x<=mid)ans+=query(t[last].ls,t[p].ls,x,y,l,mid);
	if(y>mid)ans+=query(t[last].rs,t[p].rs,x,y,mid+1,r);
	return ans;
}
int main(){
	// freopen("in.in","r",stdin),freopen("out.out","w",stdout);
	std::ios::sync_with_stdio(false);std::cin.tie(0),std::cout.tie(0);
	n=read(),m=read(),q=read();
	int len=2*n-1;
	for(int i=1;i<=m;++i)
		ed[i].u=read()+1,ed[i].v=read()+1;
	Per.build(1),Wolf.build(0);
	for(int i=1;i<=Wolf.dfn_cnt;++i){
		root[i]=root[i-1];
		int x=Wolf.dfn[i];
		if(x<=n)insert(root[i-1],root[i]=++cnt,Per.lf[x],1,len);
	}
	for(int i=1;i<=q;++i){
		int u=read(),v=read(),l=read(),r=read();
		u++,v++,l++,r++;
		int start=Per.get(u,l,1),end=Wolf.get(v,r,0);
		if(query(root[Wolf.lf[end]-1],root[Wolf.rf[end]],Per.lf[start],Per.rf[start],1,len))
			std::cout<<1<<'\n';
		else std::cout<<0<<'\n';
	}
}

posted @ 2024-07-26 14:03 Ishar-zdl 阅读(73) 评论(5) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· P4899 [IOI2018] werewolf 狼人题解

· 2024年7月杂题乱写

· kruskal 重构树学习笔记

· Kruskal重构树

· 【学习笔记】(15) Kruskal 重构树

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

2025年3月

日

一

二

三

四

五

六

Ishar-zdl的博客

Kruskal 重构树学习笔记

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论

	#include<bits/stdc++.h>
	#define endl '\n'
	inline int read(){
	char ch=getchar();int x=0,f=1;
	for(;ch<'0'\|\|ch>'9';ch=getchar())if(ch=='-')f=-1;
	for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
	return x*f;
	}
	const int N=1e5+10;
	int n,m,q,fa[N],st[20][N],head[N],cnt,dfn_cnt,dfn[N],f[N],dep[N],w[N];
	bool vis[N];
	struct EDGE{int u,v,w;}ed[N];
	struct edge{int v,nex;}e[N<<1];
	inline void add(int u,int v){e[++cnt]={v,head[u]},head[u]=cnt;}
	inline bool cmp(EDGE a,EDGE b){return a.w>b.w;}
	inline int get(int x,int y){return dep[x]<dep[y]?x:y;}
	inline void dfs(int x,int fa){
	vis[x]=1;
	st[0][dfn[x]=++dfn_cnt]=x;f[x]=fa;dep[x]=dep[fa]+1;
	for(int i=head[x];i;i=e[i].nex)dfs(e[i].v,x);
	}
	inline int LCA(int u,int v){
	if(u==v)return u;
	if((u=dfn[u])>(v=dfn[v]))std::swap(u,v);
	int d=std::__lg(v-u++);
	return f[get(st[d][u],st[d][v-(1<<d)+1])];
	}
	inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
	inline void Kruskal(){
	for(int i=1;i<=2*n;++i)fa[i]=i;
	std::stable_sort(ed+1,ed+m+1,cmp);
	int _new=n;
	for(int i=1;i<=m&&cnt<=2*n-2;++i){
	int u=find(ed[i].u),v=find(ed[i].v);
	if(u==v)continue;
	++_new;add(_new,u),add(_new,v);
	fa[u]=fa[v]=_new;
	w[_new]=ed[i].w;
	}
	for(int i=_new;i;--i)
	if(!vis[i])dfs(i,0);
	n*=2;
	for(int i=1;i<=std::__lg(n);++i)
	for(int j=1;j+(1<<i)-1<=n;++j)
	st[i][j]=get(st[i-1][j],st[i-1][j+(1<<i-1)]);
	}
	inline void work(int u,int v){
	if(find(u)!=find(v)){std::cout<<-1<<'\n';return;}
	std::cout<<w[LCA(u,v)]<<'\n';
	}
	int main(){
	// freopen("in.in","r",stdin),freopen("out.out","w",stdout);
	std::ios::sync_with_stdio(false);
	std::cin.tie(0),std::cout.tie(0);
	n=read(),m=read();
	for(int i=1;i<=m;++i)ed[i].u=read(),ed[i].v=read(),ed[i].w=read();
	Kruskal();
	q=read();
	for(int i=1,u,v;i<=q;++i)u=read(),v=read(),work(u,v);
	}