Edu EFG [41 -> 60]
如题。在补题解ing。
觉得放代码可能会卡死,考虑到这个,这一篇就不放代码了。
edu 41
E

显然是主席树,枚举一个 \(j\) 然后找一下 \(1 ~ a_j\) 这段区间有多少个大于等于 \(j\) 的,就做完了吧,答案记得除掉2。
F

这个显然是 \(border\) 吧,然后我们考虑用哈希快速判断两个串是否相等。
倒着枚举,你会发现每次最多增长2,如果没有增长的话直接往下减,复杂度易证。
G

斯特林数,会了再更。
edu 42
E

性质题,有空做。
F

一个连通块是一个环,点数 = 边数。所以我们找一下点双和点双内的边数。然后直接压入栈中,随便搞一下就好了。
G
5 人过的题,不做。
edu 43
先鸽子了,这场没有G(((
edu 44
E

排个序,随便贪心吧。
F

想了几分钟就会了。
我们考虑一个字母在这个区间的出现状况,用 01 表示,区间的 01 用哈希值表示。
考虑搞 26 次,如果对于一个字母有一个和它对应的哈希值,那么这个是可行的。
G

鸽子。
edu 45
E
鸽子(没翻译)
F

鸽子。
G

这个没鸽子。
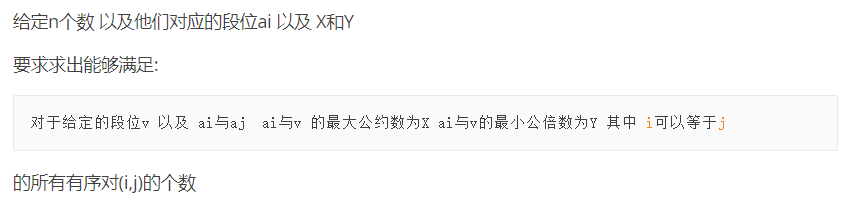
\([1, 2e5]\) 约数个数非常少。
然后我们对于每个约数,算一次 \(\gcd\) 为这个数的倍数的个数,然后这个统计下来可以用莫比乌斯函数容斥一下,就做完了。
edu 46
E

必经边只有非强连通分量的边,所以缩点之后求一下直径就好了。
F

1.莫队+栈,中间有个数少了就拿栈顶填上去。
2.还可以扫描线,维护一下上一个出现的位置,然后找一个上一个出现位置在 \([1,l-1]\) 的就可以了吧(口胡
G
树形dp,暂时还不会。
edu 47
E

先考虑推一下柿子,首先是 在中途,还有一个是最后一段,然后就做完了,乘上每一个的系数。
F

长链剖分或者线段树合并都可以吧,随便转移就是了。
G

Hall 定理+贪心,从前向后从小到大的顺序贪心,并判断后面能不能完美匹配,是否合法,这样就做完了。
edu 48
E

咕咕咕。
F

咕咕咕。
G
rho+FWT。
代码还没写,再说。(意思还是咕了。
edu 49
这场先鸽子着。
edu 50
E

\(n^2\)暴力一下,求一下交点,去重之后加到答案中。
F

这个有奇怪做法,正经做法建议去找个blog学莫比乌斯反演的容斥。
考虑贡献最多的其实是 \(x^3\) 这种形式,我们这类单独计算,其他的拿来搞搞就好了。
然后去重,二分,即可,复杂度和空间都可以。
G
13 个人过,先鸽了。
edu 51
E
时间久远,不记得当时写了啥, 有空想吧,先鸽了。
F
多了 20 条边的树。
对多余的点跑最短路就好了。
G
edu 52
鸽子一场。
edu 53
E

简单数位dp,状压一下即可。
F

不会,鸽了。
G

这个写过,到时候放博客链接。
edu 54
E

离线,差分,做完了。
F
没看过题,以后再说
G
3 个人过,鸽了。
edu 55
E

考虑分治,做完了。
F
没看过题,以后再说
G
没看过题,以后再说
edu 56
E
以前写过,以后放链接。
F

简单容斥,\(f_{i,j}\) 表示 \(i\) 这个数为 \(j\) 的方案数。
G

求的是最大两点距离。
\(|x - y|\) 的正负考虑,如果最大的话,一定都是正数,所以拆开来 \(2^k\) 种情况,直接取最大的就行了。
然后线段树的每个区间表示成这个区间的答案,更新的话考虑取最大值。
edu 57
E

考虑一下这个东西怎么做,我们枚举第一个人的分数,然后假设有几个比他大的,算一下,然后简单容斥,就做完了,总方案数用隔板法,就可以轻松得出。
F

简单题,随便做。
G

忘记之前怎么做的了,以后说(
edu 58
E
...
F
考虑一下单调性,就可以省掉一个部分的复杂度。
G
简单线性基。
edu 59
F
简单区间dp。




