强联通分量学习笔记

过于丢人，现在才写出来学习笔记(，这玩意挺简单的其实。

前置知识，递归。

不太想画图，那就简单画画。

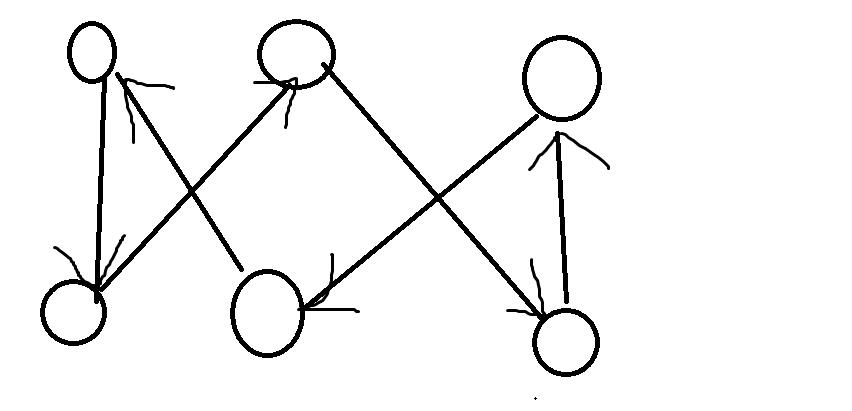
这张图就是一个强联通分量，定义就是这样，一堆有向边（也可以无向边，那就是加两条有向边嘛233）

从任意的 x 点 可以走到 任意的 y 点 则 x,y 属于同一个强联通分量。

首先需要一个 \(dfn[]\) , \(low[]\) , 以及一个栈 ， 还有染色标号的数组记为 \(col[]\)

dfn 越小，那么越先被遍历。
那么如果没有 \(dfn[v]\) 的说明没有遍历下去啊，就可以一直递归下去，直到没有找到没有被标记 \(dfn\) 的为止
同样，一路递归，一路拿 low 记录你能到的最小值[判断条件:未入栈，未被染色]，最小值具有传递性，所以可以通过 \(low_u == dfn_v\) 来判断是否遍历完能到的。

P2341 【模板】强连通分量 / [HAOI2006]受欢迎的牛

#include<cstdio>

using namespace std ;

int n , m ;
const int N = 1e4 + 10 ;
const int M = 5e4 + 10 ;
struct node {
	int v ;
	int nxt ;
} e[M << 1] ;
int head[N] , cnt = 0 ;
inline void Add(int u , int v) {
	e[++ cnt].v = v ;
	e[cnt].nxt = head[u] ;
	head[u] = cnt ;
	return ;
}
int dfn[N] , low[N] , co[N] ;
int idx = 0 ;
int st[N] ;
int tot = 0 ;
int top = 0 ;
int size[N] ;
inline int min(int x , int y) {
	return x < y ? x : y ;
}
inline void Tarjan(int u) {
	dfn[u] = low[u] = ++ idx ;
	st[++ top] = u ;
	for(register int i = head[u] ; i ; i = e[i].nxt) {
		int v = e[i].v ;
		if(! dfn[v]) {
			Tarjan(v) ;
			low[u] = min(low[u] , low[v]) ;
		}
		else if (! co[v]) low[u] = min(low[u] , dfn[v]) ;
	}
	if(low[u] == dfn[u]) {
		co[u] = ++ tot ;
		++ size[tot] ;
		while(st[top] ^ u) {
			++ size[tot] ;
			co[st[top --]] = tot ;
		}
		top -- ;
	}
	return ;
}

int degree[N] ;
signed main() {
	scanf("%d %d " , & n , & m) ;
	for(register int i = 1 ; i <= m ; i ++) {
		int u , v ;
		scanf("%d %d" , & u , & v) ;
		Add(u , v) ;
	}
	for(register int i = 1 ; i <= n ; i ++) 
		if(! dfn[i]) Tarjan(i) ;
	for(register int i = 1 ; i <= n ; i ++)
		for(register int j = head[i] ; j ; j = e[j].nxt) {
			if(co[i] ^ co[e[j].v]) degree[co[i]] ++ ;
		}
	int ans = 0 ;
	cnt = 0 ;
	for(register int i = 1 ; i <= tot ; i ++)
		if(! degree[i]) ans = i , cnt ++ ;
	if(cnt == 1) return ! printf("%d\n" , size[ans]) ;
	else printf("%d\n" , 0) ;
	return 0 ;	
}

题目挺多的，找找就完事了。