点分治[学习笔记]
部分借鉴 : bzt学长的blog
点分治,顾名思义,就是分治树上的一堆点…
点分治的话…就是处理某一类形如树上路径小于/等于?
既然是分治,我们肯定每一次都要选择一个点,从他开始分治下去。那么考虑我们如何选择这个点呢?我们发现,每一次处理完一个点之后,我们都要递归进它的子树,那么时间复杂度受到它最大的子树的大小的影响。比如,如果原树是一条链,我们选择链首,一路递归下去,时间复杂度毫无疑问是O(n2)的(那还不如别学了直接打暴力)。所以,我们要让每一次选到的点的最大子树最小。实际上,一棵树的最大子树最小的点有一个名称,叫做重心。
考虑一下为什么每一次都选择重心,时间复杂度就是对的呢?
因为重心有一个很重要的性质,每一个子树的大小都不超过\(\frac{n}{2}\)
考虑为什么呢?我们可以用反证法来证明
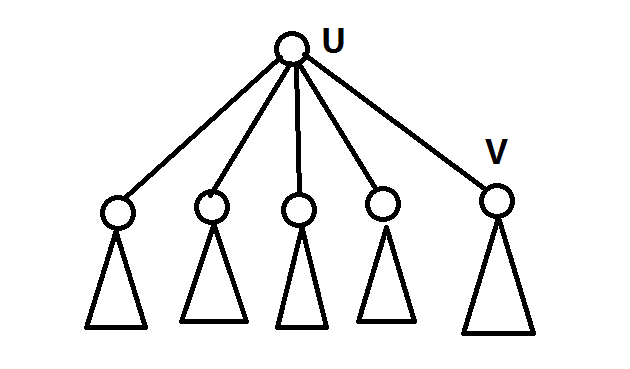
考虑有如上这么一棵树,其中点u是重心,\(son_u\)表示\(u\)点的最大的子树的大小,\(v\)是点\(u\)的最大子树,且\(size_v>\frac{size_u}{2}\)
因为\(size_v>\frac{size_u}{2}\),其他子树加上点\(u\)的节点数小于size[u]/2,那么不难发现,我们选择点\(v\)作为重心,son[v]=size[v]−1<son[u],那么很明显u不满足重心的定义
于是每一次找到重心,递归的子树大小是不超过原树大小的一半的,那么递归层数不会超过O(\(\log n\))层,时间复杂度为O(\(n\log n\))
找重心的代码……
inline void find(int u , int fa) {
size[u] = 1 ; mx[u] = 0 ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ; if(v == fa || vis[v]) continue ; find(v , u) ;
size[u] += size[v] ; cmax(mx[u] , size[v]) ;
} cmax(mx[u] , S - size[u]) ;
if(mx[u] < mx[rt]) { rt = u ; }
}
然后每次累加贡献
inline void divide(int u) {
solve(u , 0 , 1) ;
vis[u] = 1 ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) continue ;
solve(v , e[i].w , -1) ;
S = size[u] ; rt = 0 ; mx[0] = n ;
find(v , u) ;
divide(rt) ;
}
}
标记上原来的重心 然后重新在子树内找…
放几道题?。。
// Isaunoya
#include<bits/stdc++.h>
using namespace std ;
using LL = long long ;
using uint = unsigned int ;
#define int long long
#define fir first
#define sec second
#define pb push_back
#define mp(x , y) make_pair(x , y)
template < typename T > inline void read(T & x) { x = 0 ; int f = 1 ; register char c = getchar() ;
for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
x *= f ;
}
template < typename T > inline void print(T x) {
if(! x) { putchar('0') ; return ; }
static int st[105] ;
if(x < 0) putchar('-') , x = -x ;
int tp = 0 ;
while(x) st[++ tp] = x % 10 , x /= 10 ;
while(tp) putchar(st[tp --] + '0') ;
}
template < typename T > inline void print(T x , char c) { print(x) ; putchar(c) ; }
template < typename T , typename ...Args > inline void read(T & x , Args & ...args) { read(x) ; read(args...) ; }
template < typename T > inline void sort( vector < T > & v) { sort(v.begin() , v.end()) ; return ; }
template < typename T > inline void unique( vector < T > & v) { sort(v) ; v.erase(unique(v.begin() , v.end()) , v.end()) ; }
template < typename T > inline void cmax(T & x , T y) { if(x < y) x = y ; return ; }
template < typename T > inline void cmin(T & x , T y) { if(x > y) x = y ; return ; }
const int Mod = LLONG_MAX ;
inline int QP(int x , int y) { int ans = 1 ;
for( ; y ; y >>= 1 , x = (x * x) % Mod)
if(y & 1) ans = (ans * x) % Mod ;
return ans ;
}
template < typename T > inline T gcd(T x , T y) { if(y == 0) return x ; return gcd(y , x % y) ; }
template < typename T > inline T lcm(T x , T y) { return x * y / gcd(x , y) ; }
template < typename T > inline void mul(T & x , T y) { x = 1LL * x * y ; if(x >= Mod) x %= Mod ; }
template < typename T > inline void add(T & x , T y) { if((x += y) >= Mod) x -= Mod ; }
template < typename T > inline void sub(T & x , T y) { if((x -= y) < 0) x += Mod ; }
int n , m ;
int rt ;
const int N = 1000000 + 5 ;
int size[N] ;
int cnt = 0 , head[N] ; int S ;
struct node { int v , nxt , w ; } e[N << 1] ;
inline void add(int u , int v , int w) { e[++ cnt].v = v ; e[cnt].w = w ; e[cnt].nxt = head[u] ; head[u] = cnt ; return ; }
int mx[N] ;
int vis[N] ;
inline void find(int u , int fa) {
size[u] = 1 ; mx[u] = 0 ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ; if(v == fa || vis[v]) continue ; find(v , u) ;
size[u] += size[v] ; cmax(mx[u] , size[v]) ;
} cmax(mx[u] , S - size[u]) ;
if(mx[u] < mx[rt]) { rt = u ; }
}
int ans[N] , dis[N] , tot = 0 , a[N * 10] ;
inline void getdis(int u , int len , int fa) {
dis[++ tot] = a[u] ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v] || v == fa) continue ;
a[v] = len + e[i].w ;
getdis(v , len + e[i].w , u) ;
}
}
inline void solve(int s , int len , int w) {
tot = 0 ;
a[s] = len ;
getdis(s , len , 0) ;
for(register int i = 1 ; i <= tot ; i ++)
for(register int j = i + 1 ; j <= tot ; j ++)
ans[dis[i] + dis[j]] += w ;
}
inline void divide(int u) {
solve(u , 0 , 1) ;
vis[u] = 1 ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) continue ;
solve(v , e[i].w , -1) ;
S = size[u] ; rt = 0 ; mx[0] = n ;
find(v , u) ;
divide(rt) ;
}
}
signed main() {
read(n , m) ;
for(register int i = 1 ; i < n ; i ++) {
int x , y , z ; read(x , y , z) ;
add(x , y , z) ; add(y , x , z) ;
}
S = n ; mx[0] = n ; rt = 0 ;
find(1 , 0) ;
divide(rt) ;
for(register int i = 1 ; i <= m ; i ++) {
int k ; read(k) ; puts(ans[k] ? "AYE" : "NAY") ;
}
return 0 ;
}
// Isaunoya
#include<bits/stdc++.h>
using namespace std ;
using LL = long long ;
using uint = unsigned int ;
#define int long long
#define fir first
#define sec second
#define pb push_back
#define mp(x , y) make_pair(x , y)
template < typename T > inline void read(T & x) { x = 0 ; int f = 1 ; register char c = getchar() ;
for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
x *= f ;
}
template < typename T > inline void print(T x) {
if(! x) { putchar('0') ; return ; }
static int st[105] ;
if(x < 0) putchar('-') , x = -x ;
int tp = 0 ;
while(x) st[++ tp] = x % 10 , x /= 10 ;
while(tp) putchar(st[tp --] + '0') ;
}
template < typename T > inline void print(T x , char c) { print(x) ; putchar(c) ; }
template < typename T , typename ...Args > inline void read(T & x , Args & ...args) { read(x) ; read(args...) ; }
template < typename T > inline void sort( vector < T > & v) { sort(v.begin() , v.end()) ; return ; }
template < typename T > inline void unique( vector < T > & v) { sort(v) ; v.erase(unique(v.begin() , v.end()) , v.end()) ; }
template < typename T > inline void cmax(T & x , T y) { if(x < y) x = y ; return ; }
template < typename T > inline void cmin(T & x , T y) { if(x > y) x = y ; return ; }
const int Mod = LLONG_MAX ;
inline int QP(int x , int y) { int ans = 1 ;
for( ; y ; y >>= 1 , x = (x * x) % Mod)
if(y & 1) ans = (ans * x) % Mod ;
return ans ;
}
template < typename T > inline T gcd(T x , T y) { if(y == 0) return x ; return gcd(y , x % y) ; }
template < typename T > inline T lcm(T x , T y) { return x * y / gcd(x , y) ; }
template < typename T > inline void mul(T & x , T y) { x = 1LL * x * y ; if(x >= Mod) x %= Mod ; }
template < typename T > inline void add(T & x , T y) { if((x += y) >= Mod) x -= Mod ; }
template < typename T > inline void sub(T & x , T y) { if((x -= y) < 0) x += Mod ; }
inline int gcd(int x , int y) {
return y == 0 ? x : gcd(y , x % y) ;
}
int n ;
const int N = 2e5 + 10 ;
struct node { int v , nxt , w ; } e[N] ;
int head[N] , cnt = 0 ;
inline void add(int u ,int v , int w ) { e[++ cnt].v = v ; e[cnt].nxt = head[u] ; head[u] = cnt ; e[cnt].w = w ; }
int sum ;
int size[N] , rt = 0 ;
int mx[N] ;
bool vis[N] ;
inline void getrt(int u , int fa) {
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa) continue ;
if(vis[v]) continue ;
getrt(v , u) ;
size[u] += size[v] ;
cmax(mx[u] , size[v]) ;
}
cmax(mx[u] , sum - size[u]) ;
if(mx[u] <= mx[rt]) rt = u ;
return ;
}
int book[5] ;
int dis[N] ;
inline void getdis(int u , int fa) {
++ book[dis[u] % 3] ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v] || v == fa) continue ;
dis[v] = (dis[u] + e[i].w) ;
getdis(v , u) ;
}
}
inline int getans (int u , int w) { book[0] = book[1] = book[2] = 0 ;
// memset(book , 0 , sizeof(book)) ;
dis[u] = w % 3 ;
getdis(u , 0) ;
return book[2] * book[1] * 2 + book[0] * book[0] ;
} int ans = 0 ;
inline void solve(int u) {
vis[u] = 1 ;
ans += getans(u , 0) ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) continue ;
ans -= getans(v , e[i].w % 3) ;
rt = 0 ; sum = size[v] ;
getrt(v , u) ; solve(v) ;
}
}
signed main() {
read(n) ; mx[0] = n ;
for(register int i = 1 ; i <= n - 1 ; i ++) {
int u , v , w ; read(u , v , w) ;
add(u , v , w) ;
add(v , u , w) ;
} getrt(1 , 0) ; solve(rt) ;
int g = gcd(n * n , ans) ;
print(ans / g , '/') ;
print(n * n / g , '\n') ;
return 0 ;
}
这题不用考虑消除贡献 因为\(min\)不方便去掉也不满足可加性可减性…
#include <cstdio>
#include <cstring>
using ll = long long ;
using namespace std ;
#define reg register
inline int max(reg int x , reg int y) { return x > y ? x : y ; }
inline int min(reg int x , reg int y) { return x < y ? x : y ; }
inline int read() {
reg int x = 0 , f = 1 ; char c = getchar() ;
while(c < '0' || c > '9') { if(c == '-') f = -1 ; c = getchar() ; }
while(c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c & 15) ; c = getchar() ; }
return x * f ;
}
template < class T > void print(T x , char c = '\n') {
static char _st[100] ; int _stp = 0 ;
if(x == 0) { putchar('0') ; }
if(x < 0) { putchar('-') ; x = -x ; }
while(x) { _st[++ _stp] = (x % 10) ^ 48 ; x /= 10 ; }
while(_stp) { putchar(_st[_stp --]) ; }
putchar(c) ;
}
constexpr int N = 2e5 + 20 ;
constexpr int K = 1e6 + 10 ;
constexpr int INF = 1e9 ;
struct Edge {
int v , nxt , w ;
Edge () {}
Edge ( int _v , int _nxt , int _w ): v(_v) , nxt(_nxt) , w(_w) {}
} e[N << 1] ;
int n , k , head[N] , cnt = 0 ;
int rt = 0 , tot , sz[N] , son[N] , mn[K] , cntd = 0 , ans = INF , dis[N] , dis2[N] ;
bool vis[N] ;
inline void add(reg int u , reg int v , reg int w) { e[++ cnt] = Edge ( v , head[u] , w ) ; head[u] = cnt ; }
void getroot(reg int u , reg int fa) {
sz[u] = 1 ; son[u] = 0 ;
for(reg int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa || vis[v]) { continue ; }
getroot(v , u) ; sz[u] += sz[v] ; son[u] = max(son[u] , sz[v]) ;
}
son[u] = max(son[u] , tot - sz[u]) ;
if(son[u] < son[rt]) { rt = u ; }
}
void getdis(reg int u , reg int fa , reg int d1 , reg int d2) {
if(d1 > k) { return ; }
dis[++ cntd] = d1 ; dis2[cntd] = d2 ;
for(reg int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa || vis[v]) { continue ; }
getdis(v , u , d1 + e[i].w , d2 + 1) ;
}
}
inline void getans(reg int u) {
mn[cntd = 0] = 0 ;
for(reg int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) { continue ; }
int dd = cntd ; getdis(v , u , e[i].w , 1) ;
for(reg int j = dd + 1 ; j <= cntd ; j ++) { ans = min(ans , mn[k - dis[j]] + dis2[j]) ; }
for(reg int j = dd + 1 ; j <= cntd ; j ++) { mn[dis[j]] = min(mn[dis[j]] , dis2[j]) ; }
}
for(reg int i = 1 ; i <= cntd ; i ++) mn[dis[i]] = INF ;
}
void getall(reg int u) {
vis[u] = 1 ; getans(u) ;
for(reg int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) { continue ; }
tot = sz[v] ; rt = 0 ;
getroot(v , u) ; getall(rt) ;
}
}
int main() {
n = read() ; k = read() ;
for(reg int i = 2 ; i <= n ; i ++) {
reg int u = read() , v = read() , w = read() ;
++ u ; ++ v ; add(u , v , w) ; add(v , u , w) ;
}
son[0] = tot = n ; ++ son[0] ;
getroot(1 , 0) ;
memset(mn , 0x3f , sizeof(mn)) ;
getall(rt) ;
if(ans >= n) print(-1) ;
else print(ans) ;
return 0 ;
}
求多少条树上点对的路径小于等于\(k\)
然后考虑加贡献加起来就可以了qwq…
#include <cstdio>
#include <algorithm>
using ll = long long ;
using namespace std ;
int read() {
int x = 0 , f = 1 ; char c = getchar() ;
while(c < '0' || c > '9') { if(c == '-') f = -1 ; c = getchar() ; }
while(c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c & 15) ; c = getchar() ; }
return x * f ;
}
template < class T > void print(T x , char c = '\n') {
static char _st[100] ; int _stp = 0 ;
if(x == 0) { putchar('0') ; }
if(x < 0) { putchar('-') ; x = -x ; }
while(x) { _st[++ _stp] = (x % 10) ^ 48 ; x /= 10 ; }
while(_stp) { putchar(_st[_stp --]) ; }
putchar(c) ;
}
int n , k , tot ;
constexpr int N = 4e4 + 10 ;
struct Edge {
int v , nxt , w ;
Edge () {}
Edge (int _v , int _nxt , int _w) : v (_v) , nxt (_nxt) , w (_w) {}
} e[N << 1] ;
int cnt = 0 , head[N] , rt = 0 , sz[N] , son[N] , q[N] , l , r , dis[N] ;
bool vis[N] ; ll ans = 0 ;
void add(int u , int v , int w) { e[++ cnt] = Edge(v , head[u] , w) ; head[u] = cnt ; }
void getroot(int u , int fa) {
sz[u] = 1 ;
for(int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa || vis[v]) { continue ; }
getroot(v , u) ; sz[u] += sz[v] ;
if(sz[v] > son[u]) son[u] = sz[v] ;
}
if(tot - son[u] > son[u]) { son[u] = tot - son[u] ; }
if(son[u] < son[rt]) { rt = u ; }
}
void getdis(int u , int fa) {
q[++ r] = dis[u] ;
for(int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa || vis[v]) { continue ; }
dis[v] = dis[u] + e[i].w ;
getdis(v , u) ;
}
}
ll calc(int u , int v) {
l = 1 ; r = 0 ; dis[u] = v ;
getdis(u , 0) ; ll sum = 0 ;
sort(q + 1 , q + r + 1) ;
while(l < r) {
if(q[l] + q[r] <= k) { sum += (r - l) ; l ++ ; }
else { r -- ; }
}
return sum ;
}
void dfs(int u) {
ans += calc(u , 0) ; vis[u] = 1 ;
for(int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) { continue ; }
ans -= calc(v , e[i].w) ;
tot = sz[v] ; rt = 0 ;
getroot(v , 0) ; dfs(rt) ;
}
}
int main() {
n = read() ;
for(int i = 2 ; i <= n ; i ++) {
int u = read() , v = read() , w = read() ;
add(u , v , w) ; add(v , u , w) ;
}
k = read() ; son[rt = 0] = (tot = n) + 1 ;
getroot(1 , 0) ; dfs(rt) ;
print(ans) ;
return 0 ;
}
有个弱化版…
最后减掉小于\(k\)的部分即可…
#include <cstdio>
#include <algorithm>
using ll = long long ;
using namespace std ;
#define int long long
int read() {
int x = 0 , f = 1 ; char c = getchar() ;
while(c < '0' || c > '9') { if(c == '-') f = -1 ; c = getchar() ; }
while(c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c & 15) ; c = getchar() ; }
return x * f ;
}
template < class T > void print(T x , char c = '\n') {
static char _st[100] ; int _stp = 0 ;
if(x == 0) { putchar('0') ; }
if(x < 0) { putchar('-') ; x = -x ; }
while(x) { _st[++ _stp] = (x % 10) ^ 48 ; x /= 10 ; }
while(_stp) { putchar(_st[_stp --]) ; }
putchar(c) ;
}
int n , k , tot ;
constexpr int N = 5e4 + 10 ;
struct Edge {
int v , nxt , w ;
Edge () {}
Edge (int _v , int _nxt , int _w) : v (_v) , nxt (_nxt) , w (_w) {}
} e[N << 1] ;
int cnt = 0 , head[N] , rt = 0 , sz[N] , son[N] , q[N] , l , r , dis[N] ;
bool vis[N] ; ll ans = 0 ;
void add(int u , int v , int w) { e[++ cnt] = Edge(v , head[u] , w) ; head[u] = cnt ; }
void getroot(int u , int fa) {
sz[u] = 1 ; son[u] = 0 ;
for(int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa || vis[v]) { continue ; }
getroot(v , u) ; sz[u] += sz[v] ;
son[u] = max(son[u] , sz[v]) ;
}
son[u] = max(son[u] , tot - sz[u]) ;
if(son[u] < son[rt]) { rt = u ; }
}
void getdis(int u , int fa) {
q[++ r] = dis[u] ;
for(int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(v == fa || vis[v]) { continue ; }
dis[v] = dis[u] + e[i].w ;
getdis(v , u) ;
}
}
ll calc(int u , int v) {
r = 0 ; dis[u] = v ;
getdis(u , 0) ; ll sum = 0 ;
sort(q + 1 , q + r + 1) ;
int ll = 1 , rr = r ;
while(ll < rr) {
if(q[ll] + q[rr] <= k) { sum += (rr - ll) ; ll ++ ; }
else { rr -- ; }
}
ll = 1 ; rr = r ;
while(ll < rr) {
if(q[ll] + q[rr] < k) { sum -= (rr - ll) ; ll ++ ; }
else { rr -- ; }
}
return sum ;
}
void dfs(int u) {
ans += calc(u , 0) ; vis[u] = 1 ;
for(int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ;
if(vis[v]) { continue ; }
ans -= calc(v , e[i].w) ;
tot = sz[v] ; rt = 0 ;
getroot(v , 0) ; dfs(rt) ;
}
}
signed main() {
n = read() ; k = read() ;
for(int i = 2 ; i <= n ; i ++) {
int u = read() , v = read() , w = 1 ;
add(u , v , w) ; add(v , u , w) ;
}
son[rt = 0] = (tot = n) ;
getroot(1 , 0) ; dfs(rt) ;
print(ans) ;
return 0 ;
}




