机房颓废合集。
一把 VP 2h,我每天在机房 10h+,那我是不是每天能打 5 把啊?
\(\mathbb{ARC \ 143}\)
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 300(3) | 500(1) | 600(1) | 700 | 700 | - |
| 8:14 | 16:18 | 31:35 | 57:21 | 86:10 | - |
performance: 2706
找了近几场里面难度最平和的一场。 /kk
脑子还算清醒,但是这套题属实是送我技能树上了。
A
哈哈,WA 了三发因为不开 long long。
如果两个小的加起来都耗不完最大的,那就无解,否则每次都拿最大和次大的耗,等到三个数相同了就一起减小,发现次数就是最大数。
B
容斥算算就行了,具体做法是钦定不合法的位置用总数减去即可。
式子是 \((n^2)! - ((n - 1)^2)! \cdot n^2 \cdot \binom{n^2}{2n - 1}((n - 1)!)^2\),推导过程还算 ez。
C
博弈中跟棋操作非常常见,于是上来就把所有的 \(a_i\) 对 \((x + y)\) 取模。
然后分类讨论一下 \(a_i\) 和 \(x, y\) 的大小关系,分别统计先后手能够取的堆数,但是注意一下先后手能同时取到的情况,这时先手只能先去取这一堆才能更优。
D
这是什么?一眼二分图?
拆一下,每个点拆成入度和出度,所以这道题变成了给无向边定向,然后这题我会了。
丢一个很相似的problem。
做法是在 dfs 树上的边方向不变,返祖边从后代指向祖先。
因为性质是原图上的 \((u, v)\) 如果是桥,那么现在无论怎么连都还是桥。
如果 \(\exists u \rightarrow v, v \rightarrow u\),那么我删一条边无所谓,这是不影响连通性的。
E
又来?首先保证有解,老套路了,从叶子开始(我想了很久,为什么这一类在树上操作的题从叶子开始能很快突破,核心在于叶子节点的性质很强,只需要考虑它和它父亲的联系,后续的操作可以向上合并)如果它是白色,那么必须比它的父亲先操作,否则它会因为父节点的操作变成黑色,导致无解,反之,必须比它的父亲后操作。
于是反复利用这个性质往上合并,
这样可以把 DAG 建出来,直接优先队列贪。是否有解直接看根节点计算后颜色即可。
F
全网就没啥人过,做不动了。
\(\mathbb{ARC \ 154}\)
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 300 | 400(1) | 500(1) | (3) | - | - |
| 3:42 | 10:23 | 30:21 | - | - | - |
performance: 2133
绷,这个 D 做得确实下饭 😣 但是好消息是没做出来(这样就没有罚时了)
A
贪心换,小的全放 \(A\) ,大的全放在 \(B\) 。
B
发现操作等价于把前面 \(k\) 个拿出来随便插,那么直接判断后面的是否是 \(s\) 的子串就可以了,套二分就可以过了。
C
直接模拟即可。。。
D
这个交互有点意思,我们可以首先把 \(1\) 的位置用 \(n\) 次问出来。
问出来之后就可以 stable_sort 排序直接过了。
E
首先改写这个贡献的式子
假设我已经拿到了最后的序列,那么根据定义,每个点的贡献是
考虑这个贡献用动态的方式呈现,首先这个序列有序,对于一个位置 \(i\) ,将他右边的一个数 \(j\) 放在前面去,这个位置变成 \(i + 1\) ,此时贡献是让 \(g(i)+1\) ,反之,放一个左边的到后面去,位置变成 \(i - 1\) 贡献 \(g(i) - 1\) ,那么可以得到 \(g(i)=i(i - Q_i)\) 。
那么此时计算 \(Q_i\) 在某个位置上的期望就可以了,很容易发现,这个期望很对称,将 \(Q_i\) 放在 \(i\) 和放在 \(n - i + 1\) 这两个位置上的方案数相同,那么最后位置的期望就是 \(\frac{n + 1}{2}\) 。
F
一眼计数大炮题。
乐死我了,直接贺一张图。
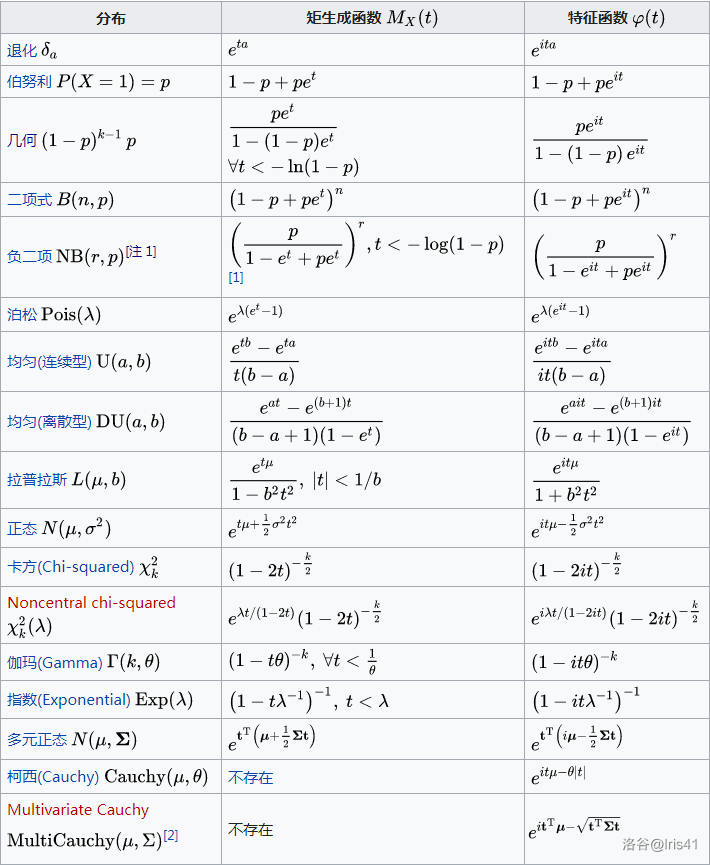
假设现在已经有 \(i\) 个面了,需要扔出第 \(i + 1\) 个面,成功的概率是 \(p = \frac{n - i}{n}\)。然后我们开始查表,这个是集合分布,于是生成函数是 \(M_x(t) = \frac{pe^t}{1 - (1 - p)e^t}\)。
然后做完了。 🤤
如果我没有表了怎么办呢???
记一个结论 \([x^k]F(e^x)\) 就是 \(k\) 次方的期望。感觉很麻烦,反正联赛不会考。
\(\mathbb{ARC \ 147}\)
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 300 | 500(1) | 600 | 700 | - | - |
| 4:29 | 68:58 | 20:22 | 36:16 | - | - |
performance: 2418
到了 68:58 才做出来 B,这是怎么回事呢? /cf
D 是猜出来的,这又是怎么回事呢? /hanx
A
最大的数在模了最小的数之后如果不被删掉,就会取代最小的数,双端队列模拟即可。
B
哈哈哈哈哈哈哈哈哈哈。
我做了 1h+。
因为使 A 操作小,我们就先用 B 操作把奇偶数位上的数排好序。然后利用 A 操作依次换即可。
于是我写了好久好久。。。
C
按左右端点排序,拆一下贡献发现 \(\Theta(n)\) 扫一遍即可。
D
直觉法,答案是 \(n^m \cdot m^{n - 1}\)。
如何直觉?首先观察到在 \(S_1\) 和 \(x\) 确定的情况下,我可以推出来其他集合。
所以固定 \(x\),感觉一下,它在或者不在 \(S_1\) 中的方案数是 \(n\),所以有 \(n^m\) 种方案,再对于 \(S_1\),有 \(m^{n - 1}\) 种方案,乘起来就是答案,感受那股劲。
E
不会了。
首先判无解的情况,把 A,B 数组排序,如果存在 \(A_i < B_i\) 那就不行。反证非常容易。
于是我们拎出来需要交换的二元组 \((A_i, B_i)\),分别塞入两个小根堆里面,把合法的 \((A_i, B_i)\) 按 \(B_i\) 从小往大排序。
每次取出来 \(x, y\),如果已经合法就不管了,否则考虑交换,按 \(B_i\) 从小往大遍历合法序列,把所有比 \(x\) 小的二元组中的 \(A_i\) 扔进大根堆,每次取一个最大的去匹配即可。
说的有点抽象,具体看代码非常好理解。
int res, n, a[MAXN], b[MAXN], pa[MAXN], pb[MAXN];
vector<pii> vec;
priority_queue<int, vector<int>, greater<int> > qa, qb;
priority_queue<int, vector<int>, less<int> > qu;
int main() {
read(n);
for (int i = 1; i <= n; i++) read(a[i], b[i]), pa[i] = a[i], pb[i] = b[i];
sort(pa + 1, pa + 1 + n), sort(pb + 1, pb + 1 + n);
for (int i = 1; i <= n; i++) if (pa[i] < pb[i]) return printf("-1\n"), 0;
for (int i = 1; i <= n; i++) {
if (a[i] < b[i]) qa.push(a[i]), qb.push(b[i]);
else vec.push_back(pii(a[i], b[i]));
}
sort(all(vec), [](const pii& x, const pii& y) { return x.second < y.second; });
for (int i = 0; !qa.empty(); ) {
int tmpa = qa.top(), tmpb = qb.top();
res++;
if (tmpa >= tmpb) { qa.pop(), qb.pop(); continue; }
for (; i < vec.size() && vec[i].second <= tmpa; i++) qu.push(vec[i].first);
qa.pop(), qa.push(qu.top()), qu.pop();
}
printf("%d\n", n - res);
return 0;
}
F
联赛前先把多项式放一放。
\(\mathbb{ARC \ 142}\)
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 300 | 500 | 600(2) | - | - | - |
| 4:39 | 9:48 | 15:56 | - | - | - |
performance: 2717
光速结束战斗,C TLE 的原因是交互题不写 fflush(stdout)。
后面三道都不会!后面三道都不会!后面三道都不会!后面三道都不会!
但是看起来好像大家都不怎么会。
A
脑瘫题,具体是翻一下然后补 \(0\) 或者直接补 \(0\),注意有可能回文或者是末尾有 \(0\) 不能翻,还要注意在翻之后的数如果小于原数就没有答案了,因为题目里面有一句”Find the minimum possible value of x after operations.“。
B
暴力换然后过了。感性理解一下这样是对的。
C
以后注意一下,交互题要在输出后马上 fflush(stdout)。
做法很好想,要找一个在 \(1,2\) 点的简单路径上的点,这样的点到 \(1, 2\) 点之间的距离和一定是最小的。
但是注意一些细节,当 \(1, 2\) 点相邻的时候这样会算出来 \(3\),如果满足条件的点只有一个或者两个点之间的距离不是 \(1\) 时答案应该是 \(1\)。
D
没做出来,我继续想一会。
其实突破口非常明显,”每条树边最多被一颗棋子经过,最终所有棋子占据的节点集合唯一“。
说明棋子一直在反复横跳,于是变成了树上对链的划分问题。
为啥想错???因为没有去手玩样例,这种性质画画图应该就能很快拿到。
至于怎么划分链,想想可以有,当棋子从 \(u\) 移动到了 \(v\),那么 \(u\) 和 \(v\) 之间连边,又因为 \(S_k = S_{(k \mod 2)}\),所以只需要考虑一步就可以了。
直接计算合法的状态不是很爽,考虑不合法的状态,对于边 \((u, v)\) 如果不存在于一条链中,则 \(u, v\) 必须是一个链头一个链尾。
然后有 \(7\) 种转移,乐死我了。
- \(x, y \in \mathrm{subtree}(u), lca(x, y) = u, u \ on \ x \rightarrow y\)
- \(x \in \mathrm{subtree}(u), x \rightarrow u\)
- \(x \in \mathrm{subtree}(u), u \rightarrow x\)
- \(x \not\in \mathrm{subtree}(u), x \rightarrow u\)
- \(x \not\in \mathrm{subtree}(u), u \rightarrow x\)
- \(x \in \mathrm{subtree}(u), y \not\in \mathrm{subtree}(u), x \rightarrow y\)
- \(x \in \mathrm{subtree}(u), y \not\in \mathrm{subtree}(u), y \rightarrow x\)
🤮
这个状态令我无法下手,所以我打开了题解。
其实也没多大优化,也就是没有考虑链的方向,这样就只有 \(4\) 种状态。
谁说这个代码简单了?????
贴一下
inline void dfs(int u, int fath) {
vector<int> son;
for (int v : G[u]) if (v != fath) dfs(v, u), son.push_back(v);
dp[u][2] = 1;
for (int v : son) dp[u][2] = (dp[u][2] * dp[v][3]) % Mod;
suf[0] = 1; for (int i = 0; i < son.size(); i++) suf[i + 1] = suf[i] * dp[son[son.size() - i - 1]][3] % Mod;
LL bas = 1;
for (int i = 0; i < son.size(); i++) {
int v = son[i];
dp[u][3] = (dp[u][3] + (dp[v][2] + dp[v][1]) % Mod * bas % Mod * suf[son.size() - i - 1] % Mod) % Mod;
bas = (bas * dp[v][3]) % Mod;
}
suf[0] = 1; for (int i = 0; i < son.size(); i++) suf[i + 1] = suf[i] * dp[son[son.size() - i - 1]][0] % Mod;
bas = 1;
for (int i = 0; i < son.size(); i++) {
int v = son[i];
dp[u][1] = (dp[u][1] + (dp[v][2] + dp[v][1]) % Mod * bas % Mod * suf[son.size() - i - 1] % Mod) % Mod;
bas = (bas * dp[v][0]) % Mod;
}
for (int i = 0; i < son.size() + 3; i++) for (int j = 0; j <= 3; j++) dp2[i][j] = 0;
dp2[0][0] = 1;
for (int i = 0; i < son.size(); i++) {
for (int j = 0; j <= 3; j++) {
if (j < 2) dp2[i + 1][j + 1] = (dp2[i + 1][j + 1] + dp2[i][j] * (dp[son[i]][1] + dp[son[i]][2]) % Mod) % Mod;
dp2[i + 1][j] = (dp2[i + 1][j] + dp2[i][j] * dp[son[i]][0] % Mod) % Mod;
}
}
dp[u][0] = dp2[son.size()][2];
LL mul = son.size() - 2;
if (mul > 0) dp[u][0] = (dp[u][0] * qpow(2, mul)) % Mod;
mul++;
if (mul > 0) dp[u][1] = (dp[u][1] * qpow(2, mul)) % Mod;
}
E / F
网络流先放放

