2023-02-NOI 春测前考试记录

To say goodbye is to die a little.

2023-02-11

总之就是十分困难。

T1 签到 (checkin)

真·签到题

我是 fw ，甚至无法下手，感谢 @cqbzly 把我教会了。

首先定义 \(S\) 表示选出来的超过题目限制的 \(a_i\) 的位置组成的集合，那么进行容斥并隔板得到答案的式子是

\[\Large (-1)^{\mid S \mid} \binom{n + m + (c - 1)\mid S \mid - \sum_{i \in S}b^i}{m} \]

解释一下这个式子的意思，对于在 \(S\) 里面的 \(a_i\) ，我们强制它们超出范围，那么 \(\forall i \in S, a_i > b^i + c\) ，也就是说 \(a_i - (b^i + c) > 0 \Rightarrow a_i - (b^i + c - 1) \ge 1\) ，于是我们调整上界 \(n\) 变成 \(n - \sum_{i \in S} (b^i + c - 1)\) ，就可以得到上式了。

现在我们令 \(A = n + m + (c - 1) \mid S \mid\) ，当我们保证 \(A \ge \sum_{i \in S} b^i\) 时，这个组合数就可以变成关于 \(\sum_{i\in S}b^i\) 的多项式。

这样做的原因很简单，只有 \(m\) 的数据范围是可以接受枚举的，那我们就把式子往 \(m\) 上靠。

然后把 \(n\) 转化成 \(b\) 进制，枚举 \(\mid S \mid\) ，这是怎么想到转进制的我真的不懂了，发现 \(\sum_{i\in S}b^i\) 的数位上都是 \(1\) ，所以我们枚举前缀的时候不用考虑负数。现在的问题是，从 \(1,2,\dots,m\) 中选 \(k\) 个数出来，记为 \(T\) ，对于每一个 \(i \in [1,m]\) 都求出 \((\sum_{j \in T} b_j)^i\) 的和，这里可以强行二项式展开 \(\Theta(n^4)\) 暴力。

然后要高精度。

T2 数据结构 (yyl)

傻逼卡常题 小清新数据结构

卡常狗能不能去死啊。

需要一点直观的感受，加上合理的猜测。非常轻松地可以知道求这个带权重心如果用点分治之类的手段会让这道题变得非常不轻松。

于是大胆地在 dfn 序上找性质，直接从重心本身的定义出发，它的子树和之后是总和的一半，加上要求深度最小的，那么答案的子树和一定严格大于总和的一半，于是直接从这个 dfn 的带权中点出发往根上面跳就可以了，往上面跳是 \(\Theta(\log n)\) 的，加上数据结构查询的 \(\Theta(\log n)\) 得到了一个两个 \(\log\) 的做法。

然后这题卡常，必须写 fenwicktree 才能过。

T3 爆搜 (dfs)

我只会 \(\Theta(2^n \mathrm{poly}(n))\) 的爆搜。

据说可以 meet in the middle 拿到很多分，但是我考场没写出来，也没有人写出来。

2023-02-18

这 Day2 怎么比 Day1 简单？但是我是暴力选手，也就没什么影响了。

T1 博弈 (game)

我很会读题，讲真的

开始没反应过来，然后突破口在于你怎么让 \(A\) 赢 \(B\) ，非常明显， \(B\) 比 \(A\) 先停下 \(A\) 就赢了（废话），为什么 \(B\) 会比 \(A\) 先停呢，因为 \(A\) 能够走的路程比 \(B\) 更长（废话 \(\times 2\)）。

然后就做完了，直接一边拓扑计算出从每个点开始能够走的最长路，做个背包就行了。

我是脑瘫，宏定义中用了位运算但是没加括号调了我 \(20min\) 。

T2 排列 (perm)

我是暴力选手

第一眼，原题，这里指 AGC059C ，第二眼，这怎么还有 \(m\) 个限制？？？

比较淡定，对着数据范围写了个 \(40pts\) 的装压先保底（结果是全场最高分），这种形如两个元素在排列中的先后顺序的限制一般会指向建图后在 DAG 上 dp ，但是限制太多，不好去刻画。

想着去再拿 \(m = 0\) 时的额外 \(30pts\) 部分分，于是写了个暴力准备乱搞猜一波结论，我暴力写错了啊啊啊啊啊啊啊！！！！1真的麻了，调了 \(20min\) 后直接放弃，避免栓死在这个上面了，结果最终都只有 \(40pts\) 了。

这个限制的转化很妙，先抄一遍原来的限制 \(\forall 1 ≤ a < b < c ≤ n\) , \((a, c)\) 处在 \((a, b)\) 和 \((b, c)\) 之间，然后可以转化成对于每一个区间不能出现 \((a,b),(b,c)\) 而不存在 \((a,c)\) 。

然后这个玩意儿有传递性，任取一个 \(i\) ，设 \(G_i\) 表示考虑前面 \(i\) 条边组成的图，那么 \(G_i\) 和 \(G_i\) 的补图都有传递性。这样的 \(G\) 恰好有 \(n!\) 个，解释一下，任取一个排列，如果 \(a<b\) 并且 \(a\) 在 \(p\) 中的位置在 \(b\) 的后面，那么连边 \((a, b)\) ，这样构造的图一定满足传递性，并且还是一个双射。

上面这个结论本该是我考试是暴力跑出来去验证的，但是我暴力挂了。。。

接下来一点做法上的小小震撼，因为合法前缀只有 \(n!\) 个，所以状态数有 \(\Theta(n!)\) 个，那么这样就可以暴力存边了，再来一个暴力转移。当一个合法 \(G\) 在加入一条边 \((a, b)\) 后仍合法，当且仅当 \(a\) 在 \(b\) 前面，加入这条边后相当于交换了 \((a, b)\) 的位置。

最后的复杂度 \(\Theta(n!n)\) 。

T3 子段和 (seg)

我是暴力选手，麻烦我自己边写暴力边动脑子

一个比较明显的做法是直接二分最后的代价，贪心地去判合法就可以了，判断的过程写在正解前一步，整个过程的复杂度是 \(\Theta(k n \log \omega)\) 其中的 \(\omega\) 表示值域范围。

这样就可以拿到 \(40pts\) 了，最大的瓶颈在于 \(k\) ，其实用暴力数据结构维护还可以拿到 \(\Theta(n^2 \log \omega)\) 拿到 \(70pts\) 但是考场上被对 \(k\) 个答案求和限制了思路。

思维上总是跳不出去，比较明显地正解的复杂度绝对与 \(k\) 无关，我也知道，但是什么都没做。

本身来说我 \(40pts\) 的思路很接近正解了，但是这个整体维护的技巧我还是很不熟练。对于 \(40pts\) 的做法是，分开考虑 \(g(k)\) ，记 \(a\) 为原数组的前缀和，首先二分答案记为 \(mid\) ，然后每一次操作相当于对一段后缀 \(-1\) ，最后要使 \(\forall i < j, a_j - a_i \le mid\) ，从前往后贪心，如果这里的 \(a_i > \lim\) ，就在这里减 \(\lim\) 次 \(1\) ，然后令 \(\lim \leftarrow \min\{\lim, a_i + mid\}\) 。

然后正解把上面这个过程整体维护了，定义这个函数 \(L(mid)\) ，维护 \(A(mid)\) 表示当前的代价，操作只会有两种。

• \(A(mid) \leftarrow A(mid) + \max\{0, a_i - L(mid)\}, L(mid) \leftarrow \max\{a_i, L(mid)\}\)
• \(L(mid) \leftarrow \min\{L(mid), mid + a_i\}\)

这样就可以直接数据结构整体维护了，启发是在处理有变元的函数求和时，注意考察这个函数是否有整体的性质，能不能同时维护来消掉枚举该变元的复杂度。

2023-02-20

嗯？我怎么犯低级错误了？！就当是攒 rp 了吧。

T1 逃生 (escape)

我是脑瘫

但是好笑的是按 \(a\) 作为关键字从小到大可以直接过。

为什么想不到？？？我真的能想起来反悔贪心这个东西吗？？？

首先按照 \(a_i + b_i\) 从小到大，如果这个人能够出去，就让他出去，否则把他扔进去替换垫在下面的 \(a_i\) 最大的人，这个直接大根堆维护就可以了。

T2 Match

ok 板题

T3 Edge

ok 原题

T4 羽未 (umi)

神题，膜拜 @wicton

还是犯了没有进一步思考的毛病。

赛时写了 \(50pts\) 的暴力，方法是直接分段，对于每一段都替换为这个段中的众数，分段方式我赛时研究了半天，更具体地来说是就是首先预处理出来每个颜色的管辖区间，暴力扫所有区间，如果 \(i\) 和 \(i + 1\) 没有被任何一个区间同时包含，则 \(i\) 这里可以作为一个分段点，于是我们对于每一段就可以很好维护了。

其实这个做法已经非常接近正解了，但是还是因为没有想到用管辖区间的覆盖次数去刻画分段点，导致我每一次修改都需要重构一遍分段，这也是这个暴力的瓶颈。

刻画分段点其实非常简单，因为上面说过了，当没有管辖区间任何一个管辖区间同时覆盖 \(i\) 和 \(i + 1\) 时这个点是分段点，那么记覆盖次数为 \(b_i\) ，当 \(b_i = 0\) 时我们就找到了分段点，这个是可以很简单地去用线段树维护的，与此同时维护众数出现的次数。

对于修改操作，无非就是某一个颜色的管辖区间的端点发生了改变，用 set 可以很轻松地维护。

最后就可以得到一个 \(\Theta((n + q) \log n)\) 的做法。

代码比较难写，所以放一下。

umi.cpp

/*
Stars in the sky, floating in darkness, soon I will fly faster than Light.
See through my eyes, time standing down, onward to space, engines stand by.
Sense loss of time Nebula’s blurring, lights flashing by Worlds Unknown.
Imminent approach, sensors reacting, soon I’m through faster Than Light.
Suddenly stop Readings come in, nothing in sight Sun glowing bright.
*/
#pragma GCC optimize("Ofast,no-stack-protector")
#pragma GCC target("avx2,fma")
#include <set>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define LL long long
#define ULL unsigned long long
using namespace std;
const int MAXN = 2e5 + 5;

template <typename T>
inline void read(T& x) {
  x = 0; int f = 1; char c = getchar(); while (c < '0' || c > '9') { if (c == '-') f = -f; c = getchar(); }
  while (c >= '0' && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); } x *= f;
}
template <typename T, typename... Args>
inline void read (T &x, Args&... Arg) { read (x), read (Arg...); }
template <typename T>
inline T Abs(T x) { return x < 0 ? -x : x; }
template <typename T>
inline T Max(T x, T y) { return x > y ? x : y; }
template <typename T>
inline T Min(T x, T y) { return x < y ? x : y; }

int n, m, maxl, a[MAXN];
set<int> q[MAXN];

struct SegmentTree {
  struct Node { int l, r, ls, rs, sum, minl, maxl, tag; } s[MAXN << 2];
  void build(int p, int l, int r) {
    s[p].l = l, s[p].r = r;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid), build(p << 1 | 1, mid + 1, r);
  }
  void push_up(int p) {
    s[p].minl = Min(s[p << 1].minl, s[p << 1 | 1].minl);
    s[p].maxl = Max(s[p << 1].maxl, s[p << 1 | 1].maxl);
    if (s[p << 1].minl < s[p << 1 | 1].minl) s[p].ls = s[p << 1].ls, s[p].sum = s[p << 1].sum, s[p].rs = Max(s[p << 1].rs, s[p << 1 | 1].maxl);
    if (s[p << 1].minl > s[p << 1 | 1].minl) s[p].rs = s[p << 1 | 1].rs, s[p].sum = s[p << 1 | 1].sum, s[p].ls = Max(s[p << 1 | 1].ls, s[p << 1].maxl);
    if (s[p << 1].minl == s[p << 1 | 1].minl) s[p].rs = s[p << 1 | 1].rs, s[p].ls = s[p << 1].ls, s[p].sum = s[p << 1].sum + s[p << 1 | 1].sum + Max(s[p << 1].rs, s[p << 1 | 1].ls);
  }
  void push_down(int p) {
    if (!s[p].tag) return;
    s[p << 1].minl += s[p].tag, s[p << 1 | 1].minl += s[p].tag;
    s[p << 1].tag += s[p].tag, s[p << 1 | 1].tag += s[p].tag;
    s[p].tag = 0;
  }
  void update1(int p, int l, int r, int k) {
    if (l > r) return;
    if (l <= s[p].l && s[p].r <= r) {
      s[p].minl += k, s[p].tag += k;
      return;
    }
    push_down(p);
    int mid = (s[p].l + s[p].r) >> 1;
    if (l <= mid) update1(p << 1, l, r, k);
    if (r > mid) update1(p << 1 | 1, l, r, k);
    push_up(p);
  }
  void update2(int p, int x, int k) {
    if (s[p].l == s[p].r) {
      s[p].maxl += k, s[p].ls += k;
      return;
    }
    push_down(p);
    int mid = (s[p].l + s[p].r) >> 1;
    if (x <= mid) update2(p << 1, x, k);
    if (x > mid) update2(p << 1 | 1, x, k);
    push_up(p);
  }
  void updateused(int col, int k) {
    int siz = q[col].size();
    if (!siz) return;
    update1(1, *q[col].begin(), *(--q[col].end()) - 1, k);
    update2(1, *q[col].begin(), k * siz);
  }
  int query() { return n - s[1].sum - s[1].ls - s[1].rs; }
} seg;

int main() {

  freopen("umi.in", "r", stdin);
  freopen("umi.out", "w", stdout);

  read(n, m);
  for (int i = 1; i <= n; i++) read(a[i]), q[a[i]].insert(i), maxl = Max(maxl, a[i]);

  seg.build(1, 1, n);
  for (int i = 1; i <= maxl; i++) if (!q[i].empty()) seg.updateused(i, 1);

  printf("%d\n", seg.query());
  for (int i = 1, x, y, col; i <= m; i++) {
    read(x, y), col = a[x];
    seg.updateused(col, -1), q[col].erase(x);
    seg.updateused(col, +1), seg.updateused(y, -1);
    q[y].insert(x), seg.updateused(y, 1), a[x] = y;
    printf("%d\n", seg.query());
  }

  return 0;
}

2023-02-21

脑洞场，没什么好补的，就记录一下考场的思路与时间分配。

T1 expand

第一眼看成生成函数题了

流汗，真的流汗了，第一眼看成生成函数题了，甚至默写了一遍 Poly 。

但是我没有直接弄出组合意义，我是写了暴力才看出来的。

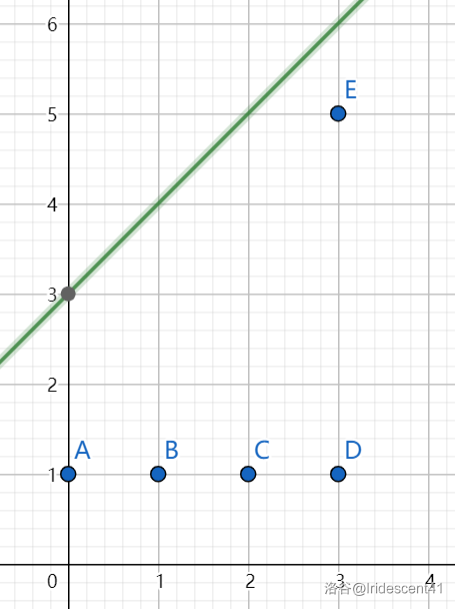
图就直接搬了，按照样例来解释一下。

可以看成从 \((0,1)\) ,\((1,1)\), \((2,1)\) ,\((3,1)\) 出发，走到 \((3,5)\)，每次向上走一格，向右走任意格，不触碰直线 \(y=x+3\) 的方案数右上走可以等价地换成向上+向右多起点可以等价地换成 \((0,0)\) 为起点所以就是以 \((0,0)\) 为起点，走到 \((3,5)\) ，每次向上或者向右走，不触碰直线\(y=x+3\) 的方案数。

T2 角谷猜想 (conj)

流汗题目

真的流汗，出题人是个什么玩意，我这辈子都做不出来这种题。

然后非常淡定，写了个 bitset 高精直接模拟，这段代码非常简单，可以贴一下。

conj.cpp

bitset<(int)5e4> add(bitset<(int)5e4> a, bitset<(int)5e4> b) {
	bitset<(int)5e4> c = a ^ b;
	bitset<(int)5e4> d = (a & b) << 1;
	if (d.count() == 0) return c;
	else return add(c, d);
}

然后获得 \(55pts\) 好成绩。有题解，但是写了跟没写一样。好的，那我当一回搬运工。

本题做法较为多样，主体思路是把 \(n\) 分成若干个长度为 \(B\) 的块，然后基于块进
行操作。这里描述一下出题人的做法：
首先，我们将奇数的操作之后紧跟一次偶数的操作，把它们看成一次操作。那么
每次操作都会减少 \(n\) 的一位（不过可能有进位）。
我们每轮选择一个 \(k = 2^t ≥ ℓ\)，然后尝试进行 \(k\) 次操作，并求出 \(k\) 次之后剩余的
结果以及遇到奇数的次数。
如果操作次数较少，即 \(k < ℓ^2\)，那么只有最后 \(k\) 位会被用到，我们直接截取最后 \(k\)
位，然后进行同样的操作即可。否则截取的效果不是特别好，我们将其分为两次 \(2^{t−1}\)
的操作，把第一次的结果给第二次进行计算即可。
考虑这一计算过程的时间复杂度。因为保证数据随机生成，所以我们可以认为遇
到奇数的次数大致为 \(\frac{ℓ}{2}\) 。而每次遇到奇数会使得结果乘上 \(3\) ，因此每轮这样的操作之后，结果大小大致为 \(3^{\frac{ℓ}{2}}=2^{\log_2 3\frac{ℓ}{2}}\) ，因此 \(ℓ\) 每次会乘上 \(\log43\) ，故在 \(Θ(\log ℓ)\)轮后必定结束。再考虑每轮操作的复杂度。对于 \(k < ℓ^2\)，有 \(T(ℓ, k) = T(2k, k) + \frac{ℓ−k}{B} > \log2 ℓ\)；对于 \(k ≤ \frac{ℓ}{2}\)，有 \(T(ℓ, k) = T(ℓ, \frac{k}{2}) + T(\log43ℓ, \frac{k}{2})\) 。
这个复杂度其实出题人不太会算，感性理解 + 打表表明总复杂度大约为 \(Θ(ℓ \log2ℓ)\) 级别的。

T3 宝藏 (treasure)

流汗题目

我要继续流汗了。暴力过了。

字面意思，暴力过了，没什么好说的，总之就是边加边判就能过。

T4 远古计算机 (computer)

全场唯一有意思的题目

subtask1

很简单，可以手动构造

node 1
read 0 a
write a 0

subtask2

斐波拉契打表前 \(44\) 项，直接 jmp 到对应行输出。

subtask3

最快的方式就是找 \(1\) 到 \(n\) 的最短路，直接跑单源最短路即可。

subtask4

考场没写完，以 \(51\) 号到 \(100\) 号为起点跑多源最短路，但是要注意加入时间戳，因为每个点可能会处理到很多条路上的信息。

subtask5

每次跑一遍都更新一遍被占用的状态，跑 \(10\) 次即可。

2023-02-23

能不能不要把暴力写挂了啊喂 😭

cricle

没有第一时间想出来。。。

我甚至是在调完杜教筛之后才回来补的这道题，算是个签到，思路很简单，直接强连通缩点然后对于每一个连通块 \(3\) 染色就可以了。

young

%%% @wicton

非常自闭，我以为这个期望是破题口，可以找到一些性质，结果这就是一道技巧性的 dp ，以前没遇到过这样的模型，这波直接卡死了。

定义 \(f(n, m)\) 表示 \(n\) 个点，\(\forall i \in [1, n], val_i \in [0, 2^m)\) ，此时所有情况最小生成树的和。

问题在于这样怎么求最小生成树，我以前做过 XOR MST ，但是我根本没有转化过来。

根据第 \(m\) 位是否是 \(1\) 将所有点分成两个集合 \(S\) ，\(T\) ，那么 \(S\) 和 \(T\) 内部一定形成最小生成树，于是我们在 \(S\) 和 \(T\) 之间找到一条最小的边将他们连起来就可以了。

上面这一段是题解，然而我一开始并不能很好的理解，更形象的理解方式是，建一棵 0/1 trie ，把所有的点权塞进去，对于一个节点，如果它又有左儿子，又有右儿子，那么则需要用一条最小的边将他们连起来。

用 \(g(S, T, m)\) 表示分成 \(S\) ，\(T\) 两个集合之后，点权在 \([0, 2^m)\) 中，此时所有情况的最小边之和。枚举 \(1\) 的个数得到

\[\Large {f(n, m) = \sum_{i = 0}^{n} \binom{n}{i} ((2^{m-1})^{n-i}}f(i,m-1) + (2^{m-1})^i f(n-i, m-1) + g(i, n - i, m - 1) + (2^{m-1})^{n + 1}) \]

我花了好长的时间才理解。。。

解释一下，首先枚举 \(1\) 的个数为 \(i\) ，先从上一层分两个集合转移过来，分别是 \((2^{m-1})^{n-i} f(i, m-1) + (2^{m-1})^i f(n-i, m-1)\) ，然后加上前面 \(m-1\) 层 的贡献 \(g(i, n-i, m)\) 和当前这两个集合连起来的贡献为 \((2^{m-1})^{n+1}\) 。

然后考虑怎么去求 \(g(S, T, m)\) ，令 \(p(S, T, m, k)\) 表示在 \(S, T, m\) 限制情况下最小的权值为 \(k\) 时的情况数，所以 \(g(S, T, m) = \sum_{k=0}^{2^{m} - 1} p(S, T, m, k)\) 。再去求这个最小边，根据第 \(m\) 划分成 \(S1, S0, T1, T0\) ，那么连边很显然是 \(S0, T0\) 或是 \(S1, T1\) 相互连边，然后递归下去即可。

simple

\(2.2h\) 才整完整道题，写题不要旷不要旷

好怪哦，这个限制，好怪哦，我再看一眼，再看一眼。 但是它既没有融化也没有爆炸

嗯，完全没有思路，那我就打个表，在我经过一系列的猜想与反复修正之后我发现一个串合法必须是它循环同构的所有串里面字典序最小的才满足，这个非常好想，手玩一下限制就发现是一个不断位移的过程，然后我发现 \(1212\) 不合法，因为位移的时候不是严格大于，而是取等，这种情况只在有循环节串里面出现。

那就可以得到这个串的所有特征了，一个没有循环节且在所有循环同构的串里面字典序里最小的串。

显然我不会去刻画字典序最小，因为求出总数后除以长度就行了，问题是求没有循环节的串的个数，直接定义 \(dp_n\) 表示长度为 \(n\) 且没有循环节的串的个数，在定义 \(f_n\) 表示长度为 \(n\) 的没有限制的串的总数，其实就是 \(10^n\) ，于是得到 \(f_n = \sum_{d \mid n} dp_{d}\) ，那么 \(dp_{n}=f_n - \sum_{d \mid n, d \not= n} dp_{d}\) ，发现这个玩意是啥，我们莫反一下， \(dp_{n} = \sum_{d\mid n}f_d \mu(\frac{n}{d})\) 。

想一下我们在求啥 \(res = \sum_{i=1}^{n} i^2 \frac{dp_{i}}{i} = \sum_{i=1}^{n}i \sum_{d\mid i}f_d \mu(\frac{i}{d}) = \sum_{d = 1}^{n}d\mu(d)\sum_{i=1}^{\frac{n}{d}} i 10^i\) 。

然后这样直接上杜教筛。

naive

妙哦

这是个经典模型，然后我不会呗。。。

你要换个角度想，定义 \(g(x, k)\) 表示有 \(k\) 个蛋，实验 \(x\) 次能够测出的最大的 \(n\) ，于是 \(g(x, k) = g(x - 1, k - 1) + g(x - 1, k)\) ，然后归纳法（打表）得出 \(g(x, k) = \sum_{1, k}\binom{x}{i}\) ，然后就可以二分了。

2023-02-27

青鱼和序列

踩

我觉得这道题只被踩了 \(25\) 次，是大家太善良了。
因为确实不该放在这个位置，说难也不难，但是一定不 noip ，在使用了操作二之后这个操作一和操作二都将变得等价，那么特判只是用操作一的情况就可以了。复杂度为 \(\Theta(n)\) 。

垃圾绑点。

青鱼和怪兽

我不会写代码

一眼二分，转移为 \(dp_{i, j} = \min\{dp_{i + 1, j} \times (1 - p) + dp_{i, j + 1} \times p + 1, mid\}, !(i=n,j=m)\) 。
注意这个地方不能用 \(mid\) 去更新 \(dp_{n, m}\) ，最后只要 \(dp_{n, m} \le mid\) 就行了。

青鱼和区间

我我我我我。。。。。。我是不会讲题的 BOT

首先定义包含 \(i\) 的所有区间的集合为 \(S_i\) ，那么可以知道 \(\forall p_1 < p_2 < p_3 < p_4\) 一定不会出现 \(S_1 = S_3 \not = S_2 = S_4\) 。

那么我们考虑去计算不合法的方案数，定义 \(dp_{i, j}\) 表示前 \(i\) 个数一共分成了 \(j\) 个段的方案数（每段中可以随意划分），那么 \(dp_{k, j + 1} = dp_{i, j} \times 2^{\binom{len}{2}}\) 其中 \(len = k - i - 1\) 。
最后计算答案的时候用总数减去不合法的方案数即可。

2023-02-28

脑洞场了属于是

序列划分 dos

你好，我是不会 t1 的小菜鸡

sbsbsbsbsbsbsbsbsbsbsbsbsbsbsbsbsbsbsbssbsbsbsbsb。
确实脑瘫，非常脑瘫，如果 \(n\) 很大，则先把前 \(2m\) 个数划分到 \(m\) 个集合中，则数的个数减小为 \(n – 2m\) 。
这大概是最关键的一步了。接下来就可以反复地把 \(2m\) 个数为一段，划分到 \(m\) 个集合中。直到 \(n\) 比较小的时候。
当 \(n\) 比较小的时候，例如 \(n≤40\) 时，则可以搜索暴力检验能否划分成 \(m\) 个相同的集合。

二进制的世界 binary

你好，我是只会暴力的小菜鸡

这道题就更神奇了，我们可以发现所有的数值域在 \([0, 2^{16})\) 以内，于是将它砍成两半，设 \(dp_{i, j}\) 表示前面 \(8\) 位为 \(i\) 的数，与某个后 \(8\) 位为 \(j\) 的数进行位运算，后 \(8\) 位的结果的最大值以及方案数，再加入一个 \(x\) 的时候，设它前 \(8\) 位为 \(a\) ，后面 \(8\) 位为 \(b\) ，只需要枚举 \(j\) ，用 \(j \ opt \ b\) 更新所有的 \(dp_{a, j}\) ，查询的时候，用所有的 \((i \ opt \ a) << 8 | dp_{i, b}\) 更新即可。

安排座位 seat

你好，我是会做小丑题的小菜鸡

唯一会做的题，我哭死。
非常简单啊，直接容斥，式子非常简单 \(\sum_{i = 0}^{n} (-1)^i i! \binom{n}{i} [(n - i)!]^2 (n - i)\) 。

最小生成树 mst

你好，我是会背模板的小菜鸡

直接默写动态最小生成树，花了我 1.5h ，然后被卡常到 85pts，因为出题人认为这个做法非常丑陋，没有用到题目的性质。
从部分分开始思考，对于一条链，把 \(1\) 类边挂在叶子节点上，\(2\) 类边放在线段树上合并，对于两个区间合起来非常容易，如果可以用两个块之间的边链接或者将他们两个都向 \(0\) 去连边，于是记录 \(0/1\) 这个维度表示是否与 \(0\) 相连即可。
然后回到原题，Kruskal 建树之后拉出几条等效链，合并即可。

2023-03-01

挂，都可以挂

失落的世界

失落的 50pts

我真的服了，好吧，我自己的问题。

二分是显然的，但是问题就在于你只能在 \([1, n]\) 里面查询，并且依赖于上一个查询，很明显，我们需要这个位置反复横跳，具体的方法我考场并没有想出来。
看了题解，其实很简单，我们可以倒着模拟一遍这个过程，从大往小反复横跳，处理出来起点和方向即可。

谜域的界外

纯纯靠猜

因为是指数，张的飞快，我们处理出来小于 \(1e18\) 的部分，然后可以非常直观地看到我们能选的一定是一个连续的段，那么非常轻易就可以维护了。

聚合的塔尖

聚合的错误

非常下饭，能把初始化写错的也没谁了。
能不能想清楚啊！！！1，在去重的时候每个点只因该保留 \(1\) 个，而不是说对于每个 pair<int, int> 保留一个，否则最后达不到 \(\sqrt{n}\) 个点。

正解是对询问分块，因为最大值超过 \(\sqrt{k}\) 的点一定不超过 \(\sqrt{n}\) 个，这一部分的点可以暴力跑，剩余的点只需要保留周围最大的 \(\sqrt{n}\) 个点就够了，这一部分可以归并预处理出来，最后的复杂度是 \(\sqrt{n}\) 。

这启示我们什么，在不好下手的时候应该从问题的规模考虑分治入手。

沉眠的回声

不会，咕