BZOJ3191或洛谷2059 [JLOI2013]卡牌游戏

BZOJ原题链接

洛谷原题链接

我们可以倒着来\(DP\)。
设\(f[i][j]\)表示剩余\(i\)个人，从庄家数起第\(j\)个人的胜率，设当前枚举到第\(k\)张牌，该情况下这一轮淘汰的位置为\(x\)，则有状态转移方程：

\(\qquad\qquad f[i][j] = f[i][j] + \dfrac{f[i - 1][i - x + j]}{m}, (x > j)\)

\(\qquad\qquad f[i][j] = f[i][j] + \dfrac{f[i - 1][j - x]}{m}, (x < j)\)

简单解释下。

1. 当\(x = j\)时，该人被淘汰，所以不用管。
   
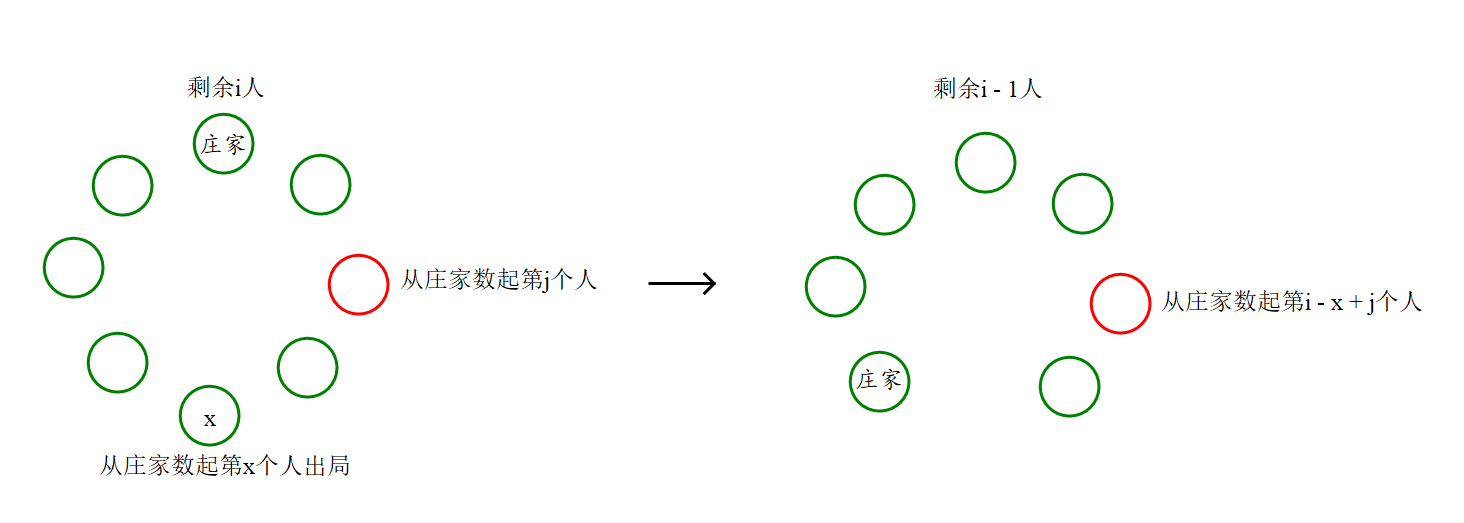
2. 当\(x > j\)时，因为庄家被淘汰的下一个人，所以当前从庄家数起第\(j\)个人就变成\(i - x + j\)个人。
   
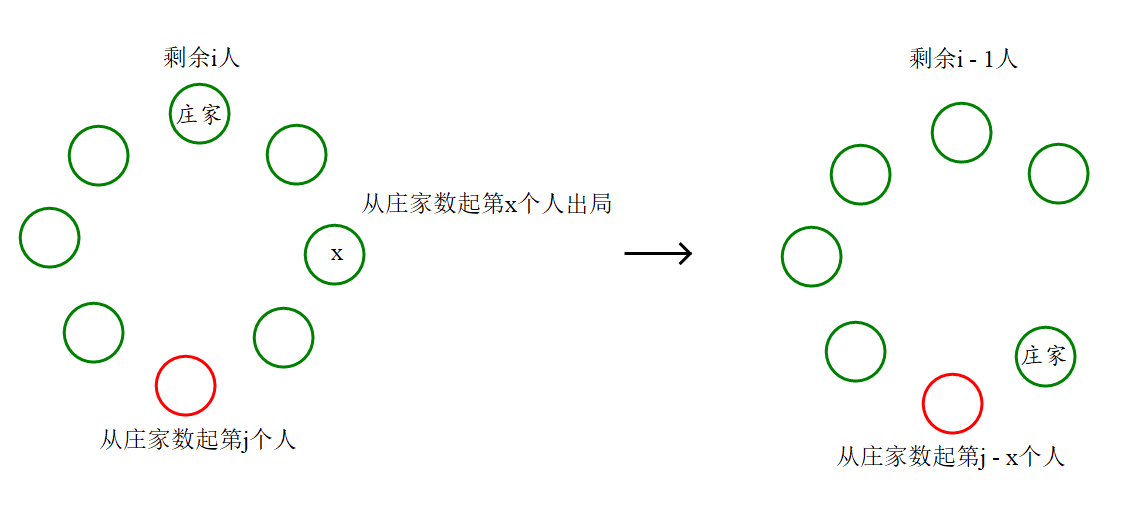
3. 当\(x < j\)时，当前从庄家数起第\(j\)个人就变成\(j - x\)个人。

因为只剩一人时，就是庄家获胜，所以\(f[1][1] = 1\)，其余为\(0\)。
最后对于从庄家数起第\(i\)个人，答案为\(f[n][i]\)。

#include<cstdio>
using namespace std;
const int N = 55;
int a[N];
double f[N][N];
inline int re()
{
	int x = 0;
	char c = getchar();
	bool p = 0;
	for (; c < '0' || c > '9'; c = getchar())
		p |= c == '-';
	for (; c >= '0' && c <= '9'; c = getchar())
		x = x * 10 + c - '0';
	return p ? -x : x;
}
int main()
{
	int i, j, k, n, m, ne;
	n = re();
	m = re();
	for (i = 1; i <= m; i++)
		a[i] = re();
	f[1][1] = 1;
	for (i = 2; i <= n; i++)
		for (j = 1; j <= i; j++)
			for (k = 1; k <= m; k++)
			{
				ne = a[k] % i ? a[k] % i : i;
				if (ne > j)
					f[i][j] += f[i - 1][i - ne + j] / m;
				else
					if (ne < j)
						f[i][j] += f[i - 1][j - ne] / m;
			}
	for (i = 1; i <= n; i++)
		printf("%.2f%% ", f[n][i] * 100);
	return 0;
}