CF Good Bye 2018

前言：这次比赛爆炸，比赛时各种想多，导致写到\(D\)题时思路已经乱了，肝了\(1\)个多小时都没肝出来，\(B\)题中途因为没开\(long\ long\)又被\(HACK\)了。。\(C\)题因为在提交前修改的一个疏忽，\(fst\)。。瞬间起飞，\(rating\)掉了\(100+\)，差点回到\(pupil \quad QAQ\)。

A. New Year and the Christmas Ornament

Description

给出\(a, b, c\)三个数，对于一个公差为\(1\)的数列\(x_1, x_2, x_3\)满足\(x_1 \leqslant a, x_2 \leqslant b, x_3 \leqslant c\)，求\(\max\{ x_1 + x_2 + x_3 \}\)。

Solution

比赛的时候有点傻，打了三个\(if\)，现在想想完全没有必要。
依次假设以\(x_1 = a, x_2 = b, x_3 = c\)，则对于每一种情况，\(x_3\)有三种值\(a + 2, b + 1, c\)，符合条件的就是对三者取\(\min\)后的那一种，最后答案就是\(\min \{ a + 2, b + 1, c \} \times 3 - 3\)。

 #include<cstdio>
using namespace std;
inline int re()
{
	int x = 0;
	char c = getchar();
	bool p = 0;
	for (; c < '0' || c > '9'; c = getchar())
		p |= c == '-';
	for (; c >= '0' && c <= '9'; c = getchar())
		x = x * 10 + c - '0';
	return p ? -x : x;
}
inline int minn(int x, int y) { return x < y ? x : y; }
int main()
{
	int a, b, c;
	a = re(); b = re(); c = re();
	printf("%d", minn(a + 2, minn(b + 1, c)) * 3 - 3);
	return 0;
}

B. New Year and the Treasure Geolocation

Description

给出\(n\)个点的坐标\(x_i, y_i\)，以及\(n\)个配对的坐标\(a_i, b_i\)，求一个坐标\((T_x, T_y)\)使得每一组坐标\(x_i, y_i\)都能找到一组配对的坐标\((a_j, b_j)\)（不能重复）满足\((x_i + a_j, y_i + b_j) = (T_x, T_y)\)。

Solution

比赛的时候还想着用\(map\)判断\(n ^ 2\)去跑，然而其实很简单，将这\(n\)个关系式全部累加，得到$$\left ( \sum \limits _{i = 1} ^ n { x_i + a_i }, \sum \limits _{i = 1} ^ n { y_i + b_i } \right ) = (n \times T_x, n \times T_y)$$

\[\therefore \begin{cases} T_x = \dfrac{\sum \limits _{i = 1} ^ n \{ x_i + a_i \}}{n} \\ T_y = \dfrac{\sum \limits _{i = 1} ^ n \{ y_i + b_i \}}{n} \end{cases} \]

记得开\(long\ long\)，我就因此被\(HACK\)了。。

#include<cstdio>
using namespace std;
inline int re()
{
	int x = 0;
	char c = getchar();
	bool p = 0;
	for (; c < '0' || c > '9'; c = getchar())
		p |= c == '-';
	for (; c >= '0' && c <= '9'; c = getchar())
		x = x * 10 + c - '0';
	return p ? -x : x;
}
int main()
{
	int i, n;
	long long x = 0, y = 0;
	n = re();
	for (i = 1; i <= n; i++)
		x += re(), y += re();
	for (i = 1; i <= n; i++)
		x += re(), y += re();
	printf("%lld %lld", x / n, y / n);
	return 0;
}

C. New Year and the Sphere Transmission

Description

有\(n\)个人围成一个圈在传球，球初始在编号为\(1\)的人手上，每次按顺时针数\(k\)个人，并将球传给他，即当前拿球的人编号为\(x\)，则球应传给编号为\(((x + k - 1) \mod n) + 1\)的人。当球再次回到\(1\)时，结束传球。
设这一轮传球顺序为\(1 \rightarrow a_1 \rightarrow a_2 \rightarrow \dots \rightarrow a_m \rightarrow 1\)，那么产生的贡献为\(1 + \sum \limits _{i = 1} ^ m a_i\)。求对于\(\forall k \in [1, n]\)，求出所有可能的不同贡献，并按从小到大输出。

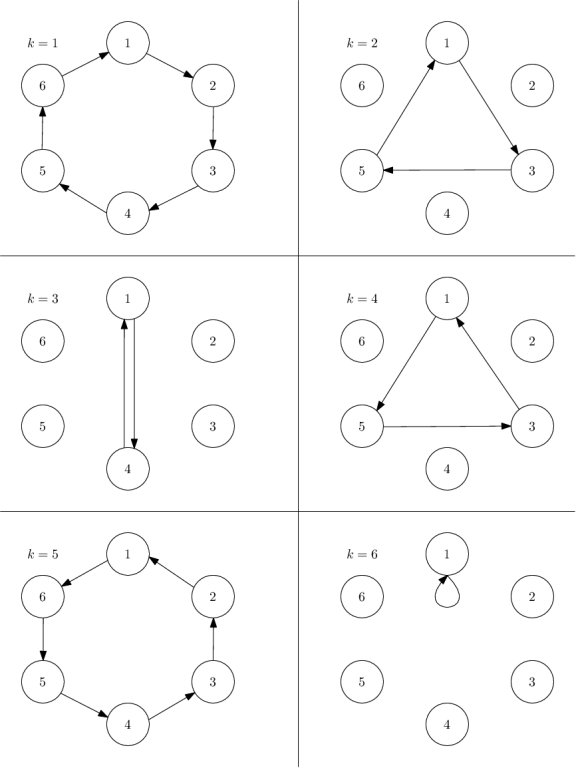
图片来自\(CF\)原题。

Solution

画几个样例后就会发现，当\(\gcd(k, n) = 1\)时，定会将所有人轮过去，贡献就是\(\sum \limits _{i = 1} ^ n i\)，只有当\(\gcd(k, n) \ne 1\)时，才会存在其它的贡献。
因为\(1\)也是\(n\)的因数，也刚好代表互质一类，所以\(n\)的因数就包含了全部可能的不同贡献，我们只需考虑因数。
而对于每一种\(k\)，很容易发现轮过的人的编号即为一个首项为\(1\)、公差为\(k\)的等差数列，由此我们可以计算出项数：\(m = \left \lfloor \dfrac{n - 1}{k} \right \rfloor + 1\)，代入等差数列求和公式：\(m \times 1 + \dfrac{(m - 1) \times m}{2} \times k\)即可得到这一中\(k\)的贡献。
将\(n\)分解因数，并计算每一个因数的贡献，最后排序一波输出即可。
然而这题我在提交前匆忙加上\(1LL\)，结果一个疏忽就\(fst\)了。。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll a[N];
inline int re()
{
	int x = 0;
	char c = getchar();
	bool p = 0;
	for (; c < '0' || c > '9'; c = getchar())
		p |= c == '-';
	for (; c >= '0' && c <= '9'; c = getchar())
		x = x * 10 + c - '0';
	return p ? -x : x;
}
int main()
{
	int i, n, x, l = 0;
	n = re();
	for (i = 1; 1LL * i * i < n; i++)
		if (!(n % i))
		{
			x = (n - 1) / i + 1;
			a[++l] = 1LL * x + ((1LL * (x - 1) * x) >> 1) * i;
			x = (n - 1) / (n / i) + 1;
			a[++l] = 1LL * x + ((1LL * (x - 1) * x) >> 1) * (n / i);
		}
	if (1LL * i * i == n)
	{
		x = (n - 1) / i + 1;
		a[++l] = 1LL * x + ((1LL * (x - 1) * x) >> 1) * i;//加1LL时忘记给完全平方的特殊情况加上去了  QAQ
	}
	sort(a + 1, a + l + 1);
	for (i = 1; i <= l; i++)
		printf("%lld ", a[i]);
	return 0;
}

D. New Year and the Permutation Concatenation

Description

设\(p\)为\(1 \sim n\)的全排列所拼成的序列，例如当\(n = 3\)时，\(p = \{ 1,2,3,1,3,2,2,1,3,2,3,1,3,1,2,3,2,1 \}\)。序列\(p\)的长度为\(n \times n!\)。
求有多少组\((i, j)\)满足\(\sum \limits _{k = i} ^ {j} p_k = \dfrac{n \times (n + 1)}{2}\)且\(1\leqslant i < j \leqslant n \times n!,\ j - i + 1 = n\)。

Solution

其实是个排列组合，然而比赛的时候肝了\(1\)个半小时都没肝出来。。
要使得连续\(n\)个数和为\(\dfrac{n \times (n + 1)}{2}\)，其实就是让这\(n\)个数不重复出现。
而连续\(n\)个数最多横跨两个排列，因此我们只需考虑连续的两个排列（不横跨的就是\(n\)个）。
要使得这\(n\)个数满足要求，则在前一排列中的后\(k\)个数必须与后一排列的后\(k\)个数相同，而对于连续的两个排列，当前一个排列的后\(k\)个数为递减，那么这两个排列的后\(k\)个数一定不相同。
至于为什么可以想想全排列产生下一个排列的方式，若后\(k\)个数是递减的，那么下一个排列定将这\(k\)个数里面的某个数与前面\(n - k\)个数里的某个数交换。简单可以理解为对于后\(k\)个数的全排列已经排完，则需要和前面的数交换一个数在再继续全排列。
因此可以计算对于当前序列的后\(k\)个数是递减的共有$A _n ^ k $种，而因为最后一个排列没有下一个排列，所以要减去\(1\)，即\(A _n ^ k - 1\)种。
对于整个\(p\)序列，取\(n\)个连续区间的方法共\(n \times n! - (n - 1)\)种，所以答案就是\(n \times n! - (n - 1) - \sum \limits _{k = 1} ^ {n - 1} \{ A_n ^ k - 1 \} = n \times n! - \sum \limits _{k = 1} ^ {n - 1} \dfrac{n!}{k!}\)。
另外，这题也有递推式：\(f(n) = (f(n − 1) + (n − 1)! − 1) \times n\)。

#include<cstdio>
using namespace std;
const int N = 1e6 + 10;
const int mod = 998244353;
int fac[N];
int main()
{
	int i, n, s = 0;
	scanf("%d", &n);
	for (fac[n] = n, i = n - 1; i; i--)
		fac[i] = 1LL * fac[i + 1] * i % mod;
	for (i = n; i > 1; i--)
		s = (1LL * s + fac[i]) % mod;
	printf("%lld", ((1LL * n * fac[1] % mod - s) % mod + mod) % mod);
	return 0;
}