10月7日考试 题解(贪心+动态规划+DFS序+分块)
T1 倾斜的线
题目大意:给定两个正整数 $P$ 和 $Q$。在二维平面上有 $n$ 个整点。现在请你找到一对点使得经过它们的直线的斜率在数值上最接近 $\frac{P}{Q}$(即这条直线的斜率与$\frac{P}{Q}$的差最小),请输出经过它们直线的斜率 $\frac{p}{q}$。如果有两组点的斜率的接近程度相同,请 输出较小的斜率。保证答案的 $\frac{p}{q}>0$,即输出的 $p$ 和 $q$ 都是正整数。
题目的要求是让$\frac{y_1-y_2}{x_1-x_2}-\frac{P}{Q}$最小,那么我们通分一下,得到:$\frac{Q(y_1-y_2)-P(x_1-x_2)}{Q(x_1-x_2)}$,然后把$(Qy-Px,Qx)$看作新的横纵坐标,按照纵坐标排个序,$O(n)$扫一下即可。
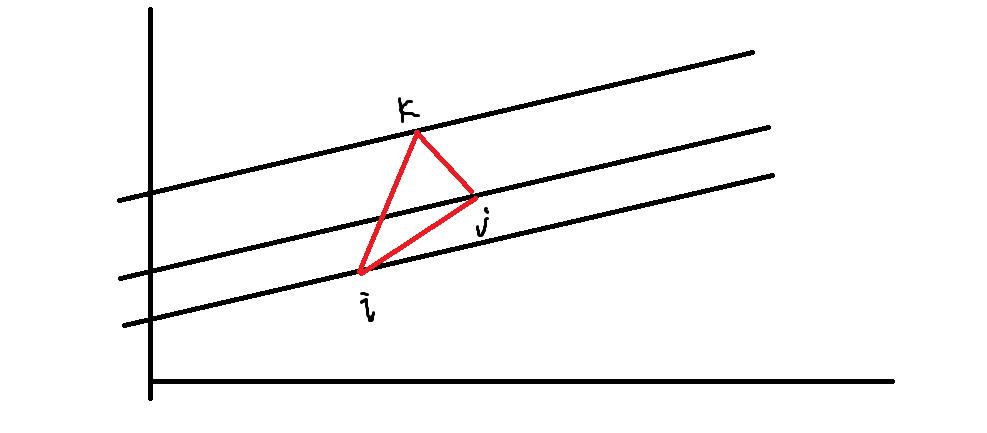
题解的做法也很妙:对于每个点,我们把斜率为$\frac{P}{Q}$且经过这些点的直线在$y$轴上的截距排序。对于一个三元组$(i,j,k)$经过$(i,j)$的直线或经过$(j,k)$的直线比经过$(i,k)$的直线更优。画出图来长这样:
时间复杂度$O(n\log n+n)$。
代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #define int long long using namespace std; const int N=200005; const int inf=1e18; int n,P,Q,ans; struct node { int id,x,y; bool operator < (const node &x) const { return y<x.y; } double operator / (const node &ff) { return (double)(ff.y-y)/(double)(ff.x-x); } }a[N],b[N]; inline int read() { int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } inline int gcd(int a,int b){ return (b==0)?a:gcd(b,a%b); } signed main() { n=read();P=read();Q=read(); for (int i=1;i<=n;i++) { a[i].x=read(),a[i].y=read(); b[i].id=i; b[i].y=a[i].y*Q-a[i].x*P; b[i].x=a[i].x*P; } sort(b+1,b+n+1); double mi=inf; for (int i=1;i<=n;i++) { if (abs(b[i]/b[i+1])<mi) ans=i,mi=abs(b[i]/b[i+1]); else if (abs(b[i]/b[i+1])==mi) ans=(b[ans+1]/b[ans])<(b[i+1]/b[i])?ans:i; } int p=abs(a[b[ans+1].id].y-a[b[ans].id].y),q=abs(a[b[ans+1].id].x-a[b[ans].id].x); int g=gcd(p,q); printf("%lld/%lld",p/g,q/g); return 0; }
T2 扭动的树
题目大意:有一棵以 $key$ 为键值以$val$ 为权值的二叉查找树,定义其某个节点的 $sum$ 为 它的子树内节点的 $val$ 之和。给出 $n$ 个$<key, val>$正整数对,现需保证这棵树上任 意一条边的两个端点的 $key$值的最大公约数不为 $1$,询问这棵树上所有节点的 $sum$ 之和最大可能是多少。如果这棵树不存在任意一个合法形态,输出$-1$。
考虑到二叉搜索树的中序遍历是一段$key$单调递增的区间,所以我们不妨以$key$为关键字从小到大排序。根据此性质,我们可以从区间中提取出一个数作为此区间的根然后区间DP。一个区间$[l,r]$的根的父亲只可能是$l-1$或者$r+1$,所以DP的状态数是$n^2$的。转移是$n^3$的。
代码:
#include<cstdio> #include<iostream> #include<algorithm> #define int long long using namespace std; const int N=305; const int inf=1e18; int n,f[N][N][2],sum[N],ans,g[N][N]; struct node { int key,val; }a[N]; inline int read() { int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } bool cmp(node x,node y) { return x.key<y.key; } inline int gcd(int a,int b){ return (b==0)?a:gcd(b,a%b); } signed main() { n=read();ans=-inf; for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) for (int k=0;k<=1;k++) f[i][j][k]=-inf; for (int i=1;i<=n;i++) a[i].key=read(),a[i].val=read(); sort(a+1,a+n+1,cmp); for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) g[i][j]=gcd(a[i].key,a[j].key); for (int i=1;i<=n;i++) { sum[i]=sum[i-1]+a[i].val; if (i!=1&&g[i][i-1]!=1) f[i][i][0]=a[i].val; if (i!=n&&g[i][i+1]!=1) f[i][i][1]=a[i].val; } for (int len=2;len<=n;len++) for (int l=1;l+len-1<=n;l++) { int r=l+len-1,res; for (int k=l;k<=r;k++) { if (k==l) res=f[l+1][r][0]+(sum[r]-sum[l-1]); else if (k==r) res=f[l][r-1][1]+(sum[r]-sum[l-1]); else res=f[l][k-1][1]+f[k+1][r][0]+(sum[r]-sum[l-1]); if (l!=1&&g[k][l-1]!=1) f[l][r][0]=max(f[l][r][0],res); if (r!=n&&g[k][r+1]!=1) f[l][r][1]=max(f[l][r][1],res); if (len==n) ans=max(ans,res); } } if (ans<0) printf("-1"); else printf("%lld",ans); return 0; }
T3 打铁的匠
题目大意:给定一棵含有$n$个结点的边带权的树,其根为$1$。一个结点的权值为根到此结点的距离。有$q$次询问,每次给出$u,k$,求以$u$为根的子树内与$u$权值之差大于等于$k$的点的差值之和。
同机房大佬写的树状数组还跑的比我快QAQ,题解写的平衡树码风感人。我自己yy出了一个分块的做法,复杂度也是正确的。先把树的$dfs$序搞出来,然后分块。预处理的同时要保证块内元素是有序的。询问时对于每个块二分找出第一个差值大于等于$k$的位置,然后前缀和搞一搞就可以了。
询问的复杂度$O(q\sqrt n \log \sqrt n)$。时限3s,卡卡常还是可以跑过去的。
代码:
#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; const int N=100005; long long ans,sum[N],g[N],b[N],w[N]; int size[N],son[N],dep[N],fa[N],n,q; int dfn[N],top[N],rev[N],tot; int belong[N],l[N],r[N],num,block; int head[N],cnt; struct node { int next,to,dis; }edge[N*2]; inline int read() { int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void add(int from,int to,int dis) { edge[++cnt]=(node){head[from],to,dis}; head[from]=cnt; } inline void dfs_son(int now,int f) { size[now]=1; dep[now]=dep[f]+1;fa[now]=f; for (int i=head[now];i;i=edge[i].next) { int to=edge[i].to; if (to==f) continue; w[to]=w[now]+edge[i].dis; dfs_son(to,now); size[now]+=size[to]; if (size[to]>size[son[now]]) son[now]=to; } } inline void dfs_chain(int now,int topf) { dfn[now]=++tot; top[now]=topf; rev[tot]=now; if (!son[now]) return; dfs_chain(son[now],topf); for (int i=head[now];i;i=edge[i].next) { int to=edge[i].to; if (dfn[to]) continue; dfs_chain(to,to); } } inline void build() { for (int i=1;i<=n;i++) b[i]=w[rev[i]]; block=sqrt(n);num=n/block; if (n%block) num++; for (int i=1;i<=n;i++) { g[i]=b[i]; belong[i]=((i-1)/block)+1; } for (int i=1;i<=num;i++) { l[i]=(i-1)*block+1; r[i]=i*block; } r[num]=n; for (int i=1;i<=num;i++) sort(g+l[i],g+r[i]+1); for (int i=1;i<=n;i++) sum[i]=sum[i-1]+g[i]; } inline void query(int x,int y,long long k) { if (belong[x]==belong[y]) { for (int i=x;i<=y;i++) if (b[i]-b[x]>=k) ans+=(b[i]-b[x]); return; } for (int i=x;i<=r[belong[x]];i++) if (b[i]-b[x]>=k) ans+=(b[i]-b[x]); for (int i=l[belong[y]];i<=y;i++) if (b[i]-b[x]>=k) ans+=(b[i]-b[x]); for (int i=belong[x]+1;i<=belong[y]-1;i++) { int L=l[i],R=r[i],mid; while(L<R) { mid=(L+R)>>1; if (g[mid]-b[x]>=k) R=mid; else L=mid+1; } if (L==r[i]){ if (g[L]-b[x]>=k) ans+=g[L]-b[x]; continue; } ans+=(sum[r[i]]-sum[L-1]-b[x]*(r[i]-L+1)); } } int main() { n=read(); for (int i=2;i<=n;i++) { fa[i]=read();int w=read(); add(fa[i],i,w);add(i,fa[i],w); } dfs_son(1,0); dfs_chain(1,1); build(); q=read(); while(q--) { ans=0; int u=read(),goal=read(); query(dfn[u],dfn[u]+size[u]-1,goal); printf("%lld\n",ans); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号