8月17日考试 题解

一周的颓废之后迎来了考试，考的一般般吧，有些错误挺啥b的。

T1

题目大意：有$n$个位置，每个位置$i$有一个$p_i$。如果经过这个位置奇数次那么就会去到$p_i$，如果是偶数次就会到$i+1$。问到$n+1$的最少步数。$1\leq p_i\leq i,n\leq 10^6$

唬人题。一开始没看到$p_i\leq i$，浪费了不少时间……

可以发现，当到达$i+1$时，前$i$个位置经过的次数必定是偶数次。然后通过打表可以发现，每到一个新位置$i$，他会把$[p_i,i]$的所有位置都走一遍。所以我们可以维护一下每个位置经过的次数维偶数所需要的步数，然后前缀和优化一下就好。时间复杂度$O(n)$。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7;
int sum[1000005],a[1000005],n,p[1000005];
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
signed main()
{
    n=read();
    for (int i=1;i<=n;i++) p[i]=read();
    a[1]=2;sum[1]=2;
    for (int i=2;i<=n;i++)
    {
        a[i]=sum[i-1]-sum[p[i]-1]+2;a[i]%=mod;
        sum[i]=sum[i-1]+a[i];
        sum[i]%=mod;
    }
    printf("%lld",(sum[n]+mod)%mod);
    return 0;
}

T2

题目大意：给定一个字符串。有单点修改，区间修改，区间询问。每次询问$[l,r]$有多少个形如$(0w0)$的子序列。$n,m\leq 5*10^4$，时限$2s$。每种操作约占总操作三分之一。

讲真一开始没什么思路。打了一个60pts的暴力。结果没看到括号爆零了……

一个常见的暴力套路就是考虑每个$w$的贡献。然而通过前缀和优化可以优化到$O(nm)$，这就已经可以过了。

考虑维护5个前缀和，分别维护形如$(,(0,(0w,(0w0,(0w0)$的子序列。每新加入一个字符，就更新一下前缀，最后输出维护$(0w0)$的前缀和就可以了。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=4294967296;
int sum[6],n,m,l,r;
char opt,a[50005];
inline void work(int l,int r)
{
    memset(sum,0,sizeof(sum));
    for (int i=l;i<=r;i++)
    {
        if (a[i]=='(') sum[1]++,sum[1]%=mod;
        if (a[i]=='0') sum[2]+=sum[1],sum[4]+=sum[3],sum[2]%=mod,sum[4]%=mod;
        if (a[i]=='w') sum[3]+=sum[2],sum[3]%=mod;
        if (a[i]==')') sum[5]+=sum[4],sum[5]%=mod;
    } 
    printf("%lld\n",(sum[5]+mod)%mod);
}
signed main()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++) cin>>a[i];
    while(m--)
    {
        cin>>opt;
        int x;char y;
        if (opt=='A') cin>>x>>y,a[x]=y;
        if (opt=='B')
        {
            cin>>l>>r>>y;
            for (int i=l;i<=r;i++) a[i]=y;
        }
        if (opt=='C') cin>>l>>r,work(l,r);
    }
    return 0;
}

T3

题目大意：给定一个$01$串，有$m$次询问，可以翻转长度为$k$的子区间，每次询问$[l,r]$的子串，问多少次操作能把子串都变为$0$。若不能输出$-1$。

不太会。有一个10pts的暴力：从左到右扫区间，遇到$1$就把以此为左端点长度为$k$的区间翻转。如果长度不够输出$-1$。时间复杂度$O(nmk)$。

优化一下可以达到$O(nm)$。我们对原串差分（异或）一下，只考虑操作的区间，外面视为$0$。每次操作就变成让$(l-1,l)$和$(r,r+1)$的异或值变为$0$。这样就省掉了$k$。

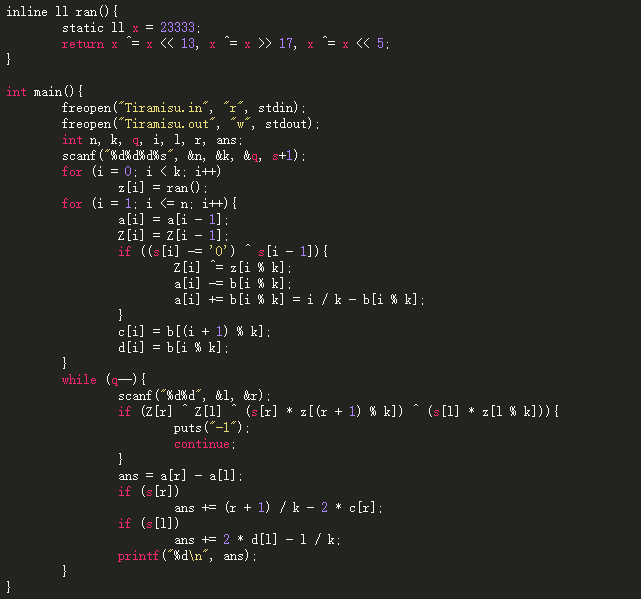
正解太玄学了，每看太懂。贴个代码吧。

--------------------------------------------------

Upd:已经写了博客。传送门：【LOJ6500】操作

代码：