7月15日考试 题解（链表+状压DP+思维题）
前言：蒟蒻太弱了，全打的暴力QAQ。
---------------------
T1 小Z的求和
题目大意：求$\sum\limits_{i=1}^n \sum\limits_{j=i}^n kth\max(a_i,a_{i+1},\cdots ,a_j)+kth\min(a_i,a_{i+1},\cdots ,a_j)$。其中$kthmax$指第$k$大，$kthmin$指第$k$小。
听hs-black说是链表维护，时间复杂度是$O(nk)$。然而并不会做……听了听学长的讲解。
对于这类问题，我们肯定是考虑每个元素对于答案的贡献的。（不然绝对会T飞
考虑$a[i]$从大到小添加，那么当有新加入的元素时，数轴为这样（假设$k=4$）：
红色为已经加入的元素，蓝色为新加入的元素，紫色是合法区间。
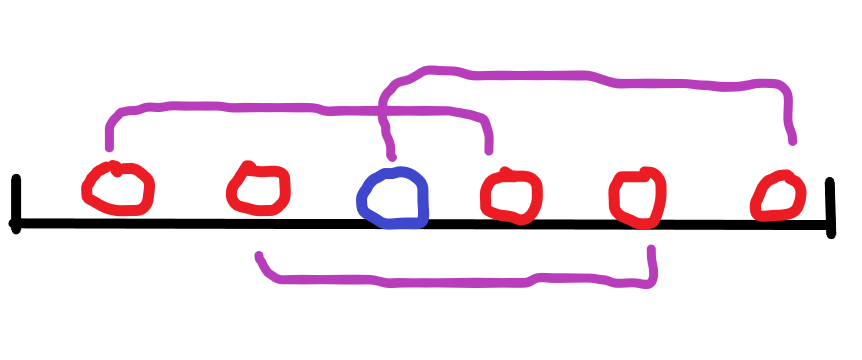
然后这个长度为$k$的区间从左到右移动，每次对于答案的贡献为$a[x]*(l-pre[l])*(nxt[r]-r)$。当所有贡献统计完后删除这个结点。
考虑到从大到小添加不易维护前驱和后缀，我们采用从小到大删除的方法，用链表维护。对于$kthmax$和$kthmin$只需相同方法求两遍就行了。时间复杂度$O(nk)$。
代码：
#include<bits/stdc++.h> #define int long long using namespace std; const int mod=998244353; int n,k,a[1000005],pos[1000005],ans; int nxt[1000005],pre[1000005]; inline int read() { int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } bool cmp(int x,int y){return a[x]<a[y];} inline void work() { for (int i=1;i<=n;i++) nxt[i]=i+1,pre[i]=i-1; for (int i=1;i<=n;i++) { int l=pos[i],r=pos[i],cnt=1; for (;cnt<k;cnt++) { if (pre[l]) l=pre[l]; else break; } for (;cnt<k;cnt++) { if (nxt[r]<=n) r=nxt[r]; else break; } if (cnt==k) { while(l<=pos[i]) { if (r==n+1) break; ans+=a[pos[i]]*(nxt[r]-r)*(l-pre[l])%mod; ans%=mod; l=nxt[l],r=nxt[r]; } } pre[nxt[pos[i]]]=pre[pos[i]]; nxt[pre[pos[i]]]=nxt[pos[i]]; } } signed main() { n=read(),k=read(); for (int i=1;i<=n;i++) a[i]=read(),pos[i]=i; sort(pos+1,pos+n+1,cmp); work(); reverse(pos+1,pos+n+1); work(); printf("%lld",ans%mod); return 0; }
T2 关押罪犯
题目大意：给定一张$n$个点，$m$条边的无向图。现在要求将这些点分成几组，每组边数不能超过$k$，且最小化分组数量。求分组最小值。
状压DP。然而我爆搜也能水不少分，$n\leq 16$。挂个$dfs$的代码吧。
代码：
#include<bits/stdc++.h> using namespace std; int n,m,k,a[20][20],ans=20; inline void dfs(int now,int cnt,int sum,int start) { if (now==n){ int tot=0; for (int i=start;i<n;i++) if (a[i][now]) tot++; if (cnt+tot<=k) ans=min(ans,sum); else ans=min(ans,sum+1); return; } int tot=0; for (int i=start;i<now;i++) if (a[i][now]) tot++; dfs(now+1,0,sum+1,now+1); if (cnt+tot<=k) dfs(now+1,cnt+tot,sum,start); } int main() { cin>>n>>m>>k; for (int i=1;i<=m;i++) { int x,y;cin>>x>>y; a[x][y]=a[y][x]=1; } dfs(1,0,1,1); cout<<ans; return 0; }
T3 CF348D Turtles
引理：LGV定理。完全不会。听wyx大佬说可以不用定理，因为只有两条路径直接做就可以。
其实是一道思维题。
题意可以简化为从$(1,2)$到$(n-1,m)$和从$(2,1)$到$(n,m-1)$的路径不相交的方案数。然后，本题的精髓来了：
如果两条路径有相交，那么可以理解为这种情况是从$(1,2)$到$(n,m-1)$和从$(2,1)$到$(n-1,m)$的路径。这种情况是不合法的。所以我们只需要一步容斥一下，那么答案就是：
$calc(1,2,n-1,m)*calc(2,1,n,m-1)-calc(1,2,n,m-1)*clac(2,1,n-1,m)$
代码难度普及-，思维难度提高+。
代码：
//calc(1,2,n-1,m)*calc(2,1,n,m-1)-calc(2,1,n-1,m)*calc(1,2,n,m-1) #include<bits/stdc++.h> #define int long long using namespace std; const int mod=1e9+7; long long n,m,f[3005][3005]; char vis[3005][3005]; inline int calc(int a,int b,int c,int d) { memset(f,0,sizeof(f)); for (int i=a;i<=c;i++) for (int j=b;j<=d;j++) { if (vis[i][j]=='.'){ if (i==a&&j==b) f[i][j]=1; else f[i][j]=(f[i-1][j]+f[i][j-1])%mod; } } return f[c][d]; } signed main() { cin>>n>>m; for (int i=1;i<=n;i++) scanf("%s",vis[i]+1); int t1=calc(1,2,n-1,m),t2=calc(2,1,n,m-1); int t3=calc(1,2,n,m-1),t4=calc(2,1,n-1,m); cout<<((t1*t2%mod-t3*t4%mod)+mod)%mod; return 0; }
