Treap

定义

• Binary Search Tree + Heap
• 用在红黑树、B+树，AVL，Splay等地方
• 保证在O(logn)内的查询

普通Treap方法类

• 插入数值 x。
• 删除数值 x(若有多个相同的数，应只删除一个)。
• 查询数值 x 的排名(若有多个相同的数，应输出最小的排名)。
• 查询排名为 x 的数值。
• 求数值 x 的前驱(前驱定义为小于 x 的最大的数)。
• 求数值 x 的后继(后继定义为大于 x 的最小的数)。

左旋与右旋

• 保持中序遍历不变
  

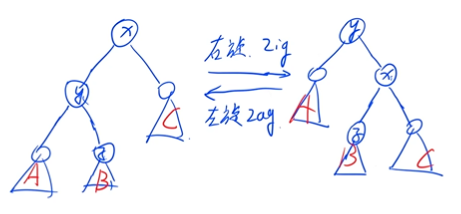
函数实现

• Node构造

struct Node{
    int l,r;
    int key,val;
    int cnt,size;
}tr[N];

• 左旋，右旋，push_up, 创建新节点

inline void push_up(int p){
    tr[p].size = tr[tr[p].r].size + tr[tr[p].l].size + tr[p].cnt;
}

inline void zig(int &p){  //右旋
    int q = tr[p].l;
    tr[p].l = tr[q].r, tr[q].r = p,p = q;
    push_up(tr[p].r),push_up(p);
}
inline void zag(int &p){ //左旋
    int q = tr[p].r;
    tr[p].r = tr[q].l,tr[q].l = p; p = q;
    push_up(tr[p].l),push_up(p);
}
int get_node(int key)
{
    tr[ ++ idx].key = key;
    tr[idx].val = rand();
    tr[idx].cnt = tr[idx].size = 1;
    return idx;
}

• 插入

void insert(int &p, int key)
{
    if (!p) p = get_node(key); //没找到，创一个新的
    else if (tr[p].key == key) tr[p].cnt ++ ; //有值,++cnt
    else if (tr[p].key > key)
    {
        insert(tr[p].l, key);
        if (tr[tr[p].l].val > tr[p].val) zig(p);  //在左边，右旋
    }
    else
    {
        insert(tr[p].r, key);
        if (tr[tr[p].r].val > tr[p].val) zag(p);  //在右边，左旋
    }
    pushup(p);     //pushup,子树发生改变
}

• 删除

void remove(int &p, int key)
{
    if (!p) return;
    if (tr[p].key == key)
    {
        if (tr[p].cnt > 1) tr[p].cnt -- ; 
        else if (tr[p].l || tr[p].r) //有子树
        {
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)  //换到右子树并栓掉
            {
                zig(p);
                remove(tr[p].r, key);
            }
            else   //换到左子树并栓掉
            {
                zag(p);
                remove(tr[p].l, key);
            }
        }
        else p = 0;
    }
    else if (tr[p].key > key) remove(tr[p].l, key);  //左查询
    else remove(tr[p].r, key); //右查询

    pushup(p);  //zig,zag
}

• 查询数值 x 的排名(若有多个相同的数，应输出最小的排名)

int get_rank_by_key(int p, int key)    // 通过数值找排名
{
    if (!p) return 0;   // 本题中不会发生此情况
    if (tr[p].key == key) return tr[tr[p].l].size + 1;
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}

• 查询排名为 x 的数值。

int get_key_by_rank(int p, int rank)   // 通过排名找数值
{
    if (!p) return INF;     // 本题中不会发生此情况
    if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);//完全左子树
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;  //结果，排除右子树
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);//在右子树
}

• 求数值 x 的前驱(前驱定义为小于 x 的最大的数)。

int get_prev(int p, int key)   // 找到严格小于key的最大数
{
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key); //左子树查找
    return max(tr[p].key, get_prev(tr[p].r, key));   //到右子树找
}

• 求数值 x 的后继(后继定义为大于 x 的最小的数)。

int get_next(int p, int key)    // 找到严格大于key的最小数
{
    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

整体代码

#include<bits/stdc++.h>
using namespace std;
const int N = 100010,INF =  1e9;
struct Node{
    int l,r;
    int key,val;
    int cnt,size;
}tr[N];

int n,root,idx;

inline void pushup(int p){
    tr[p].size = tr[tr[p].r].size + tr[tr[p].l].size + tr[p].cnt;
}

int get_node(int key)
{
    tr[ ++ idx].key = key;
    tr[idx].val = rand();
    tr[idx].cnt = tr[idx].size = 1;
    return idx;
}

inline void zig(int &p){  //右旋
    int q = tr[p].l;
    tr[p].l = tr[q].r, tr[q].r = p,p = q;
    pushup(tr[p].r),pushup(p);
}
inline void zag(int &p){ //左旋
    int q = tr[p].r;
    tr[p].r = tr[q].l,tr[q].l = p; p = q;
    pushup(tr[p].l),pushup(p);
}

void insert(int &p, int key)
{
    if (!p) p = get_node(key); //没找到，创一个新的
    else if (tr[p].key == key) tr[p].cnt ++ ; //有值,++cnt
    else if (tr[p].key > key)
    {
        insert(tr[p].l, key);
        if (tr[tr[p].l].val > tr[p].val) zig(p);  //在左边，右旋
    }
    else
    {
        insert(tr[p].r, key);
        if (tr[tr[p].r].val > tr[p].val) zag(p);  //在右边，左旋
    }
    pushup(p);     //pushup,子树发生改变
}

void remove(int &p, int key)
{
    if (!p) return;
    if (tr[p].key == key)
    {
        if (tr[p].cnt > 1) tr[p].cnt -- ; 
        else if (tr[p].l || tr[p].r) //有子树
        {
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)  //换到右子树并栓掉
            {
                zig(p);
                remove(tr[p].r, key);
            }
            else   //换到左子树并栓掉
            {
                zag(p);
                remove(tr[p].l, key);
            }
        }
        else p = 0;
    }
    else if (tr[p].key > key) remove(tr[p].l, key);  //左查询
    else remove(tr[p].r, key); //右查询

    pushup(p);  //zig,zag
}

int get_rank_by_key(int p, int key)    // 通过数值找排名
{
    if (!p) return 0;   // 本题中不会发生此情况
    if (tr[p].key == key) return tr[tr[p].l].size + 1;
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}


int get_key_by_rank(int p, int rank)   // 通过排名找数值
{
    if (!p) return INF;     // 本题中不会发生此情况
    if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);//完全左子树
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;  //结果，排除右子树
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);//在右子树
}


int get_prev(int p, int key)   // 找到严格小于key的最大数
{
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key); //左子树查找
    return max(tr[p].key, get_prev(tr[p].r, key));   //到右子树找
}


int get_next(int p, int key)    // 找到严格大于key的最小数
{
    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

int main()
{
    get_node(-INF), get_node(INF);
    root = 1, tr[1].r = 2;
    pushup(root);

    if (tr[1].val < tr[2].val) zag(root);

    scanf("%d", &n);
    while (n -- )
    {
        int opt, x;
        scanf("%d%d", &opt, &x);
        if (opt == 1) insert(root, x);
        else if (opt == 2) remove(root, x);
        else if (opt == 3) printf("%d\n", get_rank_by_key(root, x) - 1);
        else if (opt == 4) printf("%d\n", get_key_by_rank(root, x + 1));
        else if (opt == 5) printf("%d\n", get_prev(root, x));
        else printf("%d\n", get_next(root, x));
    }

    return 0;
}