约和review

使用场景

计算大数的约数个数和约数和

例子

acwing97

需要用到公式

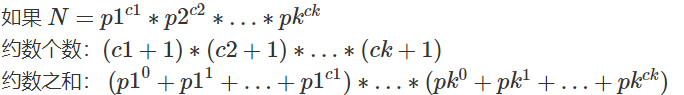
函数

个数

// ans = 1;
for (int i=2;i<=a;i++)
    {
        int s=0;
        while(a%i==0)
        {
            s++;
            a/=i;
        }
        if(s)
            ans=ans*(s+1);
    } 

求和

int ksm(int a,int b)//快速幂函数
{
    int ans=1;
    a%=Mod;
    while(b)
    {
        if (b&1)
            ans=ans%Mod*a;
        a=a%Mod*a%Mod;
        b>>=1;
    }
    return ans;
}

证明

k为奇数: sum(p,k) = (p ^ 0 + p ^ 1 + … + p^k/2 ) * (1 + p^(k/2+1) ) = sum(p,k/2) * (1 + p^(k/2+1));
k为偶数：sum(p,k) = p ^ 0 + p ^ 1 + … + p^k = 1 + p * (p^0 + p ^1 + … + p^(k-1) ) = 1 + p * sum(p,k-1);
0为1；

long long sum(int p,int c)
{
    if (c==0)
        return 1;
    if(c&1)
        return ((1+ksm(p,(c+1)>>1))*sum(p,(c-1)>>1))%Mod;//奇数的情况下
    else
        return ((1+ksm(p,c>>1))*sum(p,(c>>1)-1)+ksm(p,c))%Mod;//偶数的情况下
}

for (int i=2;i<=a;i++)
    {
        int s=0;
        while(a%i==0)
        {
            s++;
            a/=i;
        }
        if (s)
            ans=ans*sum(i,s*b)%Mod;
    } 

例子解法

分治

代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
#define Mod 9901
int a,b;
int ksm(int a,int b)//快速幂函数
{
    int ans=1;
    a%=Mod;
    while(b)
    {
        if (b&1)
            ans=ans%Mod*a;
        a=a%Mod*a%Mod;
        b>>=1;
    }
    return ans;
}
long long sum(int p,int c)
{
    if (c==0)
        return 1;
    if(c&1)
        return ((1+ksm(p,(c+1)>>1))*sum(p,(c-1)>>1))%Mod;//奇数的情况下
    else
        return ((1+ksm(p,c>>1))*sum(p,(c>>1)-1)+ksm(p,c))%Mod;//偶数的情况下
}
int main()
{
    cin>>a>>b;
    int ans=1;
    for (int i=2;i<=a;i++)
    {
        int s=0;
        while(a%i==0)
        {
            s++;
            a/=i;
        }
        if (s)
            ans=ans*sum(i,s*b)%Mod;
    } 
    if (a==0)
        cout<<0<<endl;
    else
        cout<<ans<<endl;
    return 0;
}