UCF Locals 2015

一开始在搞什么贪心，其实这个数据量就应该是搜索。先确定中心点的位置有至多49个，而其中状态不能确定的只有25个。在搜索到已经被覆盖的状态时直接往下一步走就可以了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int n, m;
char g[15][15];
char vis[15][15];

struct Cross {
    int x, y;
    int p;
    bool operator<(const Cross &c)const {
        return p < c.p;
    }
} c[60];
int ctop;

inline void update(const int &i, const int &j, int &rest) {
    ++vis[i][j];
    if(vis[i][j] == 1) {
        rest -= 1;
    }
}

inline void unupdate(const int &i, const  int &j, int &rest) {
    --vis[i][j];
    if(vis[i][j] == 0) {
        rest += 1;
    }
}

inline void Update(const int &i, const  int &j, int &rest) {
    update(i, j, rest);
    update(i + 1, j, rest);
    update(i, j + 1, rest);
    update(i - 1, j, rest);
    update(i, j - 1, rest);
}

inline void UnUpdate(const int &i, const  int &j, int &rest) {
    unupdate(i, j, rest);
    unupdate(i + 1, j, rest);
    unupdate(i, j + 1, rest);
    unupdate(i - 1, j, rest);
    unupdate(i, j - 1, rest);
}

int ans;
inline void add_cross(int i, int j) {
    if(g[i][j] != '#' || g[i - 1][j] != '#' || g[i][j - 1] != '#' || g[i + 1][j] != '#' || g[i][j + 1] != '#')
        return;
    ++ans;
    ++vis[i][j];
    ++vis[i - 1][j];
    ++vis[i][j - 1];
    ++vis[i + 1][j];
    ++vis[i][j + 1];
    ++ctop;
    c[ctop].x = i;
    c[ctop].y = j;
    c[ctop].p = min(min(i - 1, j - 1), min(n - i, m - j));
}

void dfs(int id, int cur, int rest) {
    /*printf("cur=%d\n", cur);
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= m; ++j) {
            if(g[i][j] == '.')
                printf("%c", '.');
            else {
                if(vis[i][j]) {
                    printf("%c", '*');
                } else {
                    printf("%c", '#');
                }
            }
        }
        puts("");
    }
    puts("");*/

    if(rest == 0) {
        ans = min(ans, cur);
        return;
    }

    //最优性剪枝+可行性剪枝
    if(cur + (rest + 4) / 5 >= ans)
        return;

    int x = c[id].x, y = c[id].y;

    if(id == ctop) {
        ++cur;
        Update(x, y, rest);
        if(rest == 0)
            ans = min(ans, cur);
        UnUpdate(x, y, rest);
        --cur;
        return;
    }

    int cntempty = 0;
    cntempty += (vis[x][y] == 0);
    cntempty += (vis[x - 1][y] == 0);
    cntempty += (vis[x][y - 1] == 0);
    cntempty += (vis[x + 1][y] == 0);
    cntempty += (vis[x][y + 1] == 0);

    //优化2：根据没有覆盖的格子数进行判断优先搜索左子树还是右子树，这个值低则更容易覆盖满并更新答案，但也有可能浪费一步
    if(cntempty >= 2) {
        ++cur;
        Update(x, y, rest);
        dfs(id + 1, cur, rest);
        UnUpdate(x, y, rest);
        --cur;

        dfs(id + 1, cur, rest);
    } else {
        dfs(id + 1, cur, rest);

        ++cur;
        Update(x, y, rest);
        dfs(id + 1, cur, rest);
        UnUpdate(x, y, rest);
        --cur;
    }
    return;
}

int main() {
#ifdef Yinku
    freopen("Yinku.in", "r", stdin);
#endif // Yinku
    int T;
    scanf("%d", &T);
    for(int ti = 1; ti <= T; ++ti) {
        memset(vis, 0, sizeof(vis));
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; ++i) {
            scanf("%s", g[i] + 1);
        }

        int rest = 0;
        for(int i = 1; i <= n ; ++i) {
            for(int j = 1; j <= m ; ++j) {
                if(g[i][j] == '#') {
                    ++rest;
                }
            }
        }

        ans = 0, ctop = 0;
        for(int i = 2; i <= n - 1; ++i) {
            for(int j = 2; j <= m - 1; ++j) {
                if(g[i][j] == '#') {
                    add_cross(i, j);
                }
            }
        }

        bool suc = true;
        for(int i = 1; i <= n ; ++i) {
            for(int j = 1; j <= m ; ++j) {
                if(g[i][j] == '#' && vis[i][j] == 0) {
                    suc = false;
                    break;
                }
            }
            if(!suc)
                break;
        }

        printf("Image #%d: ", ti);
        if(!suc) {
            puts("impossible");
        } else {
            memset(vis, 0, sizeof(vis));

            //最外圈的是必选的，可以立刻剪掉，搭配优化2可以将搜索的规模限制在5*5内
            int cur = 0;
            for(int j = 1; j <= m ; ++j) {
                if(g[1][j] == '#' && vis[1][j] == 0) {
                    ++cur;
                    Update(2, j, rest);
                }
                if(g[n][j] == '#' && vis[n][j] == 0) {
                    ++cur;
                    Update(n - 1, j, rest);
                }
            }
            for(int i = 1; i <= n ; ++i) {
                if(g[i][1] == '#' && vis[i][1] == 0) {
                    ++cur;
                    Update(i, 2, rest);
                }
                if(g[i][m] == '#' && vis[i][m] == 0) {
                    ++cur;
                    Update(i, m - 1, rest);
                }
            }

            //打乱相邻节点的顺序，可能是负优化因为相邻节点或许可以优先走不印
            //random_shuffle(c + 1, c + 1 + ctop);
            sort(c + 1, c + 1 + ctop);
            dfs(1, cur, rest);
            printf("%d\n", ans);
        }
        puts("");
    }
}

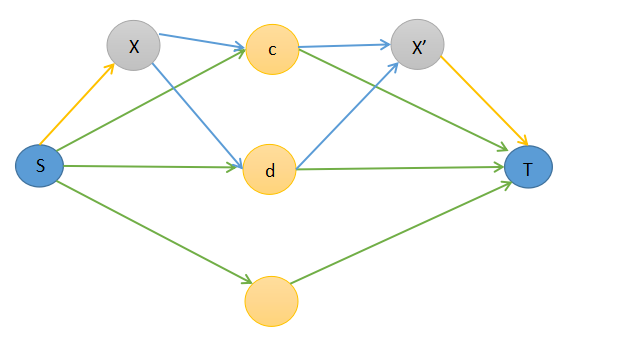
网络流，最大权闭合子图。要像下面这样建图：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

/* dinic begin */

const int MAXN = 20100;
const int MAXM = 200100;
//注意网络流要预留反向边
const int INF = 0x3f3f3f3f;
struct Edge {
    int to, next, cap, flow;
} edge[MAXM];

int tol;
int head[MAXN];

void init() {
    tol = 2;
    memset(head, -1, sizeof(head));
}

void addedge(int u, int v, int w, int rw = 0) {
    edge[tol].to = v;
    edge[tol].cap = w;
    edge[tol].flow = 0;
    edge[tol].next = head[u];
    head[u] = tol++;
    edge[tol].to = u;
    edge[tol].cap = rw;
    edge[tol].flow = 0;
    edge[tol].next = head[v];
    head[v] = tol++;
}

int Q[MAXN];
int dep[MAXN], cur[MAXN], sta[MAXN];
bool bfs(int s, int t, int n) {
    int front = 0, tail = 0;
    memset(dep, -1, sizeof(dep[0]) * (n + 1));
    dep[s] = 0;
    Q[tail++] = s;
    while(front < tail) {
        int u = Q[front++];
        for(int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i].to;
            if(edge[i].cap > edge[i].flow && dep[v] == -1) {
                dep[v] = dep[u] + 1;
                if(v == t)
                    return true;
                Q[tail++] = v;
            }
        }
    }
    return false;
}

int dinic(int s, int t, int n = -1) {
    int maxflow = 0;
    if(n == -1)
        n = t;
    n++;//假如把t作为编号最后的点的话传入t就可以了
    while(bfs(s, t, n)) {
        for(int i = 0; i < n; i++)
            cur[i] = head[i];
        int u = s, tail = 0;
        while(cur[s] != -1) {
            if(u == t) {
                int tp = INF;
                for(int i = tail - 1; i >= 0; i--) {
                    tp = min(tp, edge[sta[i]].cap - edge[sta[i]].flow);

                }
                maxflow += tp;
                for(int i = tail - 1; i >= 0; i--) {
                    edge[sta[i]].flow += tp;
                    edge[sta[i] ^ 1].flow -= tp;
                    if(edge[sta[i]].cap - edge[sta[i]].flow == 0)
                        tail = i;
                }
                u = edge[sta[tail] ^ 1].to;

            } else if(cur[u] != -1 && edge[cur[u]].cap > edge[cur[u]].flow
                      && dep[u] + 1 == dep[edge[cur[u]].to]) {
                sta[tail++] = cur[u];
                u = edge[cur[u]].to;
            } else {
                while(u != s && cur[u] == -1) {
                    u = edge[sta[--tail] ^ 1].to;
                }
                cur[u] = edge[cur[u]].next;
            }
        }
    }
    return maxflow;
}

/* dinic end */


int main() {
#ifdef Yinku
    freopen("Yinku.in", "r", stdin);
#endif // Yinku
    int T;
    scanf("%d", &T);
    for(int ti = 1; ti <= T; ++ti) {
        int n;
        scanf("%d", &n);
        double tmp;
        init();
        int sum = 0;
        for(int i = 1; i <= n; ++i) {
            scanf("%lf", &tmp);
            int t = round(tmp * 100);
            addedge(0, i, t);
            sum += t;
            //cout << t << endl;
        }
        for(int i = 1; i <= n; ++i) {
            scanf("%lf", &tmp);
            int t = round(tmp * 100);
            addedge(i, n + n * n + n * n + 1, t);
            sum += t;
            //cout << t << endl;
        }
        for(int i = 1; i <= n; ++i) {
            for(int j = 1; j <= n; ++j) {
                scanf("%lf", &tmp);
                int t = round(tmp * 100);
                addedge(n + (i - 1)*n + j, i, INF);
                addedge(n + (i - 1)*n + j, j, INF);
                addedge(0,  n + (i - 1)*n + j, t);
                sum += t;
                //cout << t << endl;
                addedge(i,  n + n * n + (i - 1)*n + j, INF);
                addedge(j,  n + n * n + (i - 1)*n + j, INF);
                addedge(n + n * n + (i - 1)*n + j,  n + n * n + n * n + 1, t);
                sum += t;
            }
        }

        //cout << "sum=" << sum << endl;
        printf("%.2f\n", (sum - dinic(0,  n + n * n + n * n + 1)) / 100.0);
    }
}