机器学习中的梯度下降和反向传播算法
本文不详细解释梯度下降和反向传播算法的具体过程，但会引用相应较好的博客作为参考。
本文主要对于这两者进行概念上的解释和比较。
首先解释梯度下降：具体过程可以参考这篇博客https://www.cnblogs.com/pinard/p/5970503.html
1.梯度下降是求解函数最值的一种方法，在机器学习中用于求解损失函数的最小值。
这个可以类比一元函数中求最值的过程，假设某一元函数f(x)可导，我们求解最值时，可以首先求出令f'(x)=0的点(极值点)，然后在极值点中寻找最值。
梯度下降的思想也是这样，只不过我们不是直接求出多元函数的全导数，而是在函数上任意选取一个点，求出这点的梯度(函数下降速度最快的方向导数)，其中梯度的大小是函数的变化率，梯度的方向是在这点所有方向中变化率最大的方向。然后我们朝着这个方向将起始点移动一段距离，这样函数值便下降了，最终的结果是当梯度为0时(类似导数为0)，我们便找到了一个局部最小值(类似极值点)。
机器学习之所以使用梯度下降，是因为我们最终的目标是计算出使得损失函数J(Θ)取最小值的那些Θ，所以便成了一个求解函数最小值的问题。
反向传播算法：具体过程可以参考https://blog.csdn.net/mao_xiao_feng/article/details/53048213，详细推导过程可以参考https://blog.csdn.net/u014313009/article/details/51039334和http://briandolhansky.com/blog/2013/9/27/artificial-neural-networks-backpropagation-part-4
反向传播算法是求解深度学习中损失函数的最小值的算法。其使用的方法还是梯度下降。
1. 那么为什么要单独起个名字叫反向传播呢？
这是因为在深度学习的多层网络求解梯度时，会用到求解梯度的链式法则，其实前向传播(从输入到输出计算梯度)和反向传播(从输出到输入计算梯度)都可以使用链式法则算出梯度，从而对损失函数进行优化。
之所以使用反向传播算法，是因为反向传播算法在时间复杂度上要小于前向传播，这对于训练大规模的神经网络十分重要。
2.反向传播还有一个名字叫误差逆传播算法，这里的误差指什么呢？
其实这里的误差我觉得叫做误差率更合适，首先看一下误差(率)的定义：
将损失函数对于第l层第j个神经元的中间值z的偏导数定义为误差，注意这里的zl=Θal-1 ，而不是激活函数激活后的值。
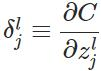
这其实只是反向传播计算过程中为了表示方便以及能够递归表示所定义的一种符号，直观的理解是第l层的误差(率)决定了这一层的中间值z'与真实值z产生偏差时，会对最终的误差C产生多大的影响。
当我们有了这个定义后，便能够简洁的表示出反向传播算法。
