矩阵微分

函数类型	向量变元 \(\mathbf{x} \in \mathbb{R}^{m}\)	矩阵变元 \(\mathbf{X} \in \mathbb{R}^{m \times n}\)
标量函数 \(f \in \mathbb{R}\)	\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}\)	\(f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}\)
向量函数 \(\mathbf{f} \in \mathbb{R}^{p}\)	\(\mathbf{f}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{p}\)	\(\mathbf{f}: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{p}\)
矩阵函数 \(\mathbf{F} \in \mathbb{R}^{p \times q}\)	\(\mathbf{F}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{p \times q}\)	\(\mathbf{F}: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{p \times q}\)

Jacobi矩阵与梯度矩阵

1. Jacobi算子：

   • 向量变元的Jacobi算子：\(\mathrm{D}_{\mathbf{x}} = \frac{\partial}{\partial \mathbf{x}^{T}} = [ \frac{\partial}{\partial x_{1}}, \frac{\partial}{\partial x_{2}}, {\dots}, \frac{\partial}{\partial x_{m}}]\)。
   • 矩阵变元的Jacobi算子：\(\mathrm{D}_{\mathbf{X}} = \frac{\partial}{\partial \mathbf{X}^{T}} = \begin{bmatrix} \frac{\partial}{\partial x_{11}},& {\dots},& \frac{\partial}{\partial x_{m1}} \\ {\vdots}, & {\ddots}, & {\vdots} \\ \frac{\partial}{\partial x_{1n}},& {\dots},& \frac{\partial}{\partial x_{mn}} \end{bmatrix}\)。

2. Jacobi矩阵：

   • 实值标量函数：对于向量变元，定义Jacobi矩阵为\(\mathrm{D}_\mathbf{x}f(\mathbf{x})\)；同理，对于矩阵变元，定义Jacobi矩阵为\(\mathrm{D}_\mathbf{X}f(\mathbf{X})\)。
   • 实值向量函数：对于向量变元，定义Jacobi矩阵为\(\mathrm{D}_\mathbf{x}\mathbf{f}(\mathbf{x})\)；同理，对于矩阵变元，定义Jacobi矩阵为\(\mathrm{D}_\mathbf{X}\mathbf{f}(\mathbf{X}){\;\triangleq\;}\mathrm{D}_{\mathrm{vec}(\mathbf{X})}\mathbf{f}(\mathbf{X})\)。
   • 实值矩阵函数：对于向量变元，定义Jacobi矩阵为\(\mathrm{D}_\mathbf{x}\mathbf{F}(\mathbf{x}){\;\triangleq\;}\mathrm{D}_\mathbf{x}\mathrm{vec}(\mathbf{F}(\mathbf{x}))\)；同理，对于矩阵变元，定义\(\mathrm{D}_\mathbf{X}\mathbf{F}(\mathbf{X}) {\;\triangleq\;} D_{\mathrm{vec}(\mathbf{X})} \mathrm{vec}(\mathbf{F}(\mathbf{X}))\)。
   • 特别地，定义矩阵变元实值标量函数\(f(\mathbf{X})\)的行偏导向量为\(\mathrm{D}_{\mathrm{vec}(\mathbf{X})}f(\mathbf{X})\)，此时，可以得到矩阵变元的Jacobi矩阵和行偏导向量之间的关系为：\(\mathrm{D}_{\mathrm{vec}(\mathbf{X})}f(\mathbf{X}) = \mathrm{rvec}(\mathrm{D}_{\mathbf{X}}f(\mathbf{X})) = (\mathrm{vec}(\mathrm{D}_{\mathbf{X}}^{T}f(\mathbf{X})))^{T}\)，即矩阵变元实值标量函数行偏导向量是Jacobi矩阵转置列向量化转置。

3. 梯度算子：

   • 向量变元的梯度算子：\({\triangledown}_{\mathbf{x}} = \frac{\partial}{\partial \mathbf{x}} = [ \frac{\partial}{\partial x_{1}}, \frac{\partial}{\partial x_{2}}, {\dots}, \frac{\partial}{\partial x_{m}}]^{T}\)。
   • 矩阵变元的梯度算子：\({\triangledown}_{\mathbf{X}} = \frac{\partial}{\partial \mathbf{X}} = \begin{bmatrix} \frac{\partial}{\partial x_{11}},& {\dots},& \frac{\partial}{\partial x_{1n}} \\ {\vdots}, & {\ddots}, & {\vdots} \\ \frac{\partial}{\partial x_{m1}},& {\dots},& \frac{\partial}{\partial x_{mn}} \end{bmatrix}\)。

4. 梯度矩阵为Jacobi矩阵的转置。

5. 计算法则：

   • 向量、矩阵变元实值标量函数的线性法则、乘积法则、除法法则与标量变元实值标量函数一致。
   • 链式法则：
     • 标量变元中介：\(\frac{\partial g(f(\mathbf{X}))}{\partial \mathbf{X}} = \frac{\partial g(y)}{\partial y} \frac{\partial y}{\partial \mathbf{X}}\)，其中，\(y=f(\mathbf{X})\)。
     • 矩阵变元中介：\([\frac{\partial g(\mathbf{F}(\mathbf{X}))}{\partial \mathbf{X}}]_{i,j} = \sum_{k=1}^{p} \sum_{l=1}^{q} \frac{\partial g(\mathbf{F}(\mathbf{X}))}{\partial [\mathbf{F}(\mathbf{X})]_{k,l}} \frac{\partial [\mathbf{F}(\mathbf{X})]_{k,l}}{\partial [\mathbf{X}]_{i, j}}\)。
   • 独立性假设：假定变元本身无特殊结构，即变元元素之间相互独立。

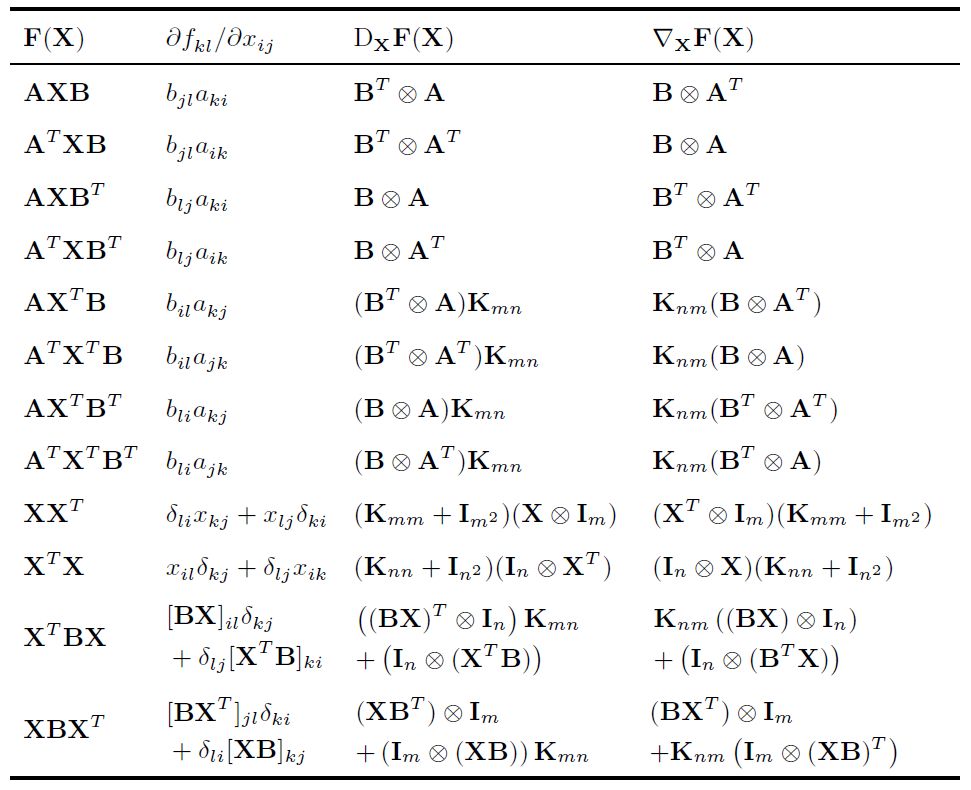
一阶实Jacobi矩阵辨识

1. 实值标量函数：对于向量变元，有\(\mathrm{d}f(\mathbf{x}) = \mathrm{tr}(\mathbf{A}\mathrm{d}\mathbf{x}) {\;\Leftrightarrow\;} \mathrm{D}_\mathbf{x}f(\mathbf{x}) = \mathbf{A}\)；同理，对于矩阵变元，有\(\mathrm{d}f(\mathbf{X}) = \mathrm{tr}(\mathbf{A}\mathrm{d}\mathbf{X}) {\;\Leftrightarrow\;} \mathrm{D}_\mathbf{X}f(\mathbf{X}) = \mathbf{A}\)。
2. 实值向量函数：对于向量变元，有\(\mathrm{d}\mathbf{f}(\mathbf{x}) = \mathbf{A}\mathrm{d}\mathbf{x} {\;\Leftrightarrow\;} \mathrm{D}_\mathbf{x}f(\mathbf{x}) = \mathbf{A}\)；同理，对于矩阵变元，有\(\mathrm{d}\mathbf{f}(\mathbf{X}) = \mathbf{A}\mathrm{d}\mathrm{vec}(\mathbf{X}) {\;\Leftrightarrow\;} \mathrm{D}_\mathbf{X}f(\mathbf{X}) = \mathbf{A}\)。
3. 实值矩阵函数：对于向量变元，有 \(\mathrm{d}\mathrm{vec}(\mathbf{F}(\mathbf{x}))=\mathbf{A}\mathrm{d}\mathbf{x} {\;\Leftrightarrow\;} \mathrm{D}_\mathbf{x}\mathbf{F}(\mathbf{x})=\mathbf{A}\)；同理，对于矩阵变元，有 \(\mathrm{d}\mathbf{F}(\mathbf{X}) = \mathbf{A}\mathrm{d}\mathbf{X}\mathbf{B} + \mathbf{C}\mathrm{d}\mathbf{X}^{T}\mathbf{D} {\;\Leftrightarrow\;} \mathrm{D}_\mathbf{X}\mathbf{F}(\mathbf{X}) = \mathbf{B}^{T}{\;\otimes\;}\mathbf{A} + (\mathbf{D}^{T}{\;\otimes\;}\mathbf{C})\mathbf{K}_{mn}\)。
4. 特别地，对于无法整理成上述形式的矩阵变元实值矩阵函数\(\mathbf{F}(\mathbf{X})\)，有\(\mathrm{d}\mathrm{vec}(\mathbf{F}(\mathbf{X}))=\mathbf{A}\mathrm{d}\mathrm{vec}(\mathbf{X})+\mathbf{B}\mathrm{d}\mathrm{vec}(\mathbf{X}^{T}){\;\Leftrightarrow\;}\mathrm{D}_\mathrm{X}\mathbf{F}(\mathbf{X})=\mathbf{A}+\mathbf{B}\mathbf{K}_{mn}\)。例如，对于\(\mathbf{F}(\mathbf{X}, \mathbf{Y})=\mathbf{X}{\;\otimes\;}\mathbf{Y}\)，有\(\mathrm{D}_\mathbf{X}\mathbf{F}(\mathbf{X}, \mathbf{Y})=(\mathbf{I}_{m}{\;\otimes\;}\mathbf{K}_{qp}{\;\otimes\;}\mathbf{I}_{n})(\mathbf{I}_{pm}{\;\otimes\;}\mathrm{vec}(\mathbf{Y}))\)和\(\mathrm{D}_\mathbf{X}\mathbf{F}(\mathbf{X}, \mathbf{Y})=(\mathbf{I}_{m}{\;\otimes\;}\mathbf{K}_{qp}{\;\otimes\;}\mathbf{I}_{n})(\mathrm{vec}(\mathbf{X}){\;\otimes\;}\mathbf{I}_{nq})\)成立，其中，有\(\mathbf{X}{\in}\mathbb{R}^{p{\times}m}\)和\(\mathbf{X}{\in}\mathbb{R}^{n{\times}q}\)。

二阶实Hessian矩阵辨识

1. 定义：对于向量变元，有\(\mathbf{H}[f(\mathbf{x})]={\triangledown}_\mathbf{x}^{2}f(\mathbf{x})={\triangledown}_\mathbf{x}(\mathrm{D}_\mathbf{x}f(\mathbf{x}))\)；同理，对于矩阵变元，有\(\mathbf{H}[f(\mathbf{X})]={\triangledown}_\mathbf{X}^{2}f(\mathbf{X})={\triangledown}_\mathbf{X}(\mathrm{D}_\mathbf{X}f(\mathbf{X}))\)。可以证明，实Hessian矩阵为对称矩阵。
2. 辨识：
   • 实值标量函数：对于向量变元，有\(\mathrm{d}^{2}f(\mathbf{x})=\mathrm{d}(\mathbf{A}\mathrm{d}\mathbf{x})=\mathrm{d}\mathbf{x}^{T}\mathbf{B}\mathrm{d}\mathbf{x}{\;\Leftrightarrow\;}\mathbf{H}[f(\mathbf{x})]=\frac{1}{2}(\mathbf{B}+\mathbf{B}^{T})\)；同理，对于矩阵变元，有\(\mathrm{d}^{2}f(\mathbf{X})=\mathrm{d}(\mathbf{A}\mathrm{d}\mathbf{x})=\mathrm{d}\mathrm{vec}(\mathbf{X})^{T}\mathbf{B}\mathrm{d}\mathrm{vec}(\mathbf{X}){\;\Leftrightarrow\;}\mathbf{H}[f(\mathbf{X})]=\frac{1}{2}(\mathbf{B}+\mathbf{B}^{T})\)。特别地，有\(\mathrm{d}^{2} f(\mathbf{X})=\mathrm{tr}(\mathbf{V}(\mathrm{d} \mathbf{X}) \mathbf{U}(\mathrm{d} \mathbf{X})^{T}) \;\Leftrightarrow\; \mathbf{H}[f(\mathbf{X})]=\frac{1}{2}(\mathbf{U}^{T} \;\otimes\; \mathbf{V}+\mathbf{U} \;\otimes\; \mathbf{V}^{T})\)和\(\mathrm{d}^{2} f(\mathbf{X})=\mathrm{tr}(\mathbf{B}(\mathrm{d} \mathbf{X}) \mathbf{C} (\mathrm{d} \mathbf{X})) \;\Leftrightarrow\; \mathbf{H}[f(\mathbf{X})]=\frac{1}{2} \mathbf{K}_{n m}(\mathbf{C}^{T} \;\otimes\; \mathbf{B}+\mathbf{B}^{T} \;\otimes\; \mathbf{C})\)成立。
   • 实值向量函数：对于向量变元，有\(\mathrm{d}^{2}\mathbf{f}(\mathbf{x})=(\mathbf{I}_{m}{\;\otimes\;}\mathrm{d}\mathbf{x})^{T}\mathbf{B}\mathrm{d}\mathbf{x}{\;\Leftrightarrow\;}\mathbf{H}[\mathbf{f}(\mathbf{x})]=\frac{1}{2}(\mathbf{B}+(\mathbf{B}^{'})_{v})\)；同理，对于矩阵变元，有\(\mathrm{d}^{2}\mathbf{f}(\mathbf{X})=(\mathbf{I}_{m}{\;\otimes\;}\mathrm{d}\mathrm{vec}\mathbf{X})^{T}\mathbf{B}\mathrm{d}\mathrm{vec}(\mathbf{X}){\;\Leftrightarrow\;}\mathbf{H}[\mathbf{f}(\mathbf{X})]=\frac{1}{2}(\mathbf{B}+(\mathbf{B}^{'})_{v})\)。其中，\(\mathbf{B}=[\mathbf{B}_{1}^{T},{\dots},\mathbf{B}_{p}^{T}]^{T}\)，\((\mathbf{B}^{'})_{v}=[\mathbf{B}_{1}, {\dots}, \mathbf{B}_{p}]^{T}\)。
   • 实值矩阵函数：对于向量变元，有\(\mathrm{d}^{2}\mathbf{F}(\mathbf{x})=(\mathbf{I}_{mp}{\;\otimes\;}\mathrm{d}\mathbf{x})^{T}\mathbf{B}\mathrm{d}\mathbf{x}{\;\Leftrightarrow\;}\mathbf{H}[\mathbf{F}(\mathbf{x})]=\frac{1}{2}(\mathbf{B}+(\mathbf{B}^{'})_{v})\)；同理，对于矩阵变元，有\(\mathrm{d}^{2}\mathbf{F}(\mathbf{X})=(\mathbf{I}_{mp}{\;\otimes\;}\mathrm{d}\mathrm{vec}\mathbf{X})^{T}\mathbf{B}\mathrm{d}\mathrm{vec}(\mathbf{X}){\;\Leftrightarrow\;}\mathbf{H}[\mathbf{F}(\mathbf{X})]=\frac{1}{2}(\mathbf{B}+(\mathbf{B}^{'})_{v})\)。其中，\(\mathbf{B}=[\mathbf{B}_{11}^{T},{\dots},\mathbf{B}_{p1}^{T}, {\dots}, \mathbf{B}_{1q}^{T},{\dots},\mathbf{B}_{pq}^{T}]^{T}\)，\((\mathbf{B}^{'})_{v}=[\mathbf{B}_{11},{\dots},\mathbf{B}_{p1}, {\dots}, \mathbf{B}_{1q},{\dots},\mathbf{B}_{pq}]^{T}\)。

共轭梯度与复Hessian矩阵

1. 复标量微分法则：\(\mathrm{d}f(z,z^{*})=\frac{\partial f(z,z^{*})}{\partial z}\mathrm{d}z+\frac{\partial f(z,z^{*})}{\partial z^{*}}\mathrm{d}z^{*}\)。

2. 复矩阵微分法则：

   • 链式法则：\(\mathrm{d} \mathrm{vec} \mathbf{F}=\frac{\partial \mathrm{vec} \mathbf{F}}{\partial(\mathrm{vec} \mathbf{Y})^{T}} \mathrm{d} \mathrm{vec} \mathbf{Y}=\frac{\partial \mathrm{vec} \mathbf{F}}{\partial(\mathrm{vec} \mathbf{Y})^{T}} \frac{\partial \mathrm{vec} \mathbf{Y}}{\partial(\mathrm{vec} \mathbf{Z})^{\mathbf{T}}} \mathrm{d} \mathrm{vec} \mathbf{Z}\)。
   • 乘法法则：\(\mathrm{d}(\mathbf{U} \mathbf{V})=(\mathrm{d} \mathbf{U}) \mathbf{V}+\mathbf{U}(\mathrm{d} \mathbf{V})\)，\(\mathrm{dvec}(\mathbf{U} \mathbf{V})=(\mathbf{V}^{T} \otimes \mathbf{I}) \mathrm{d} \mathrm{vec} \mathbf{U}+(\mathbf{I} \otimes \mathbf{U}) \mathrm{d} \mathrm{vec} \mathbf{V}\)。

3. 共轭梯度分别定义为\({\triangledown}_{\mathbf{Z}}f(\mathbf{Z},\mathbf{Z}^{*})=\mathrm{D}_{\mathbf{Z}}^{T}f(\mathbf{Z},\mathbf{Z}^{*})\)和\({\triangledown}_{\mathbf{Z}^{*}}f(\mathbf{Z},\mathbf{Z}^{*})=\mathrm{D}_{\mathbf{Z}^{*}}^{T}f(\mathbf{Z},\mathbf{Z}^{*})\)，且满足以下性质：

   • 共轭梯度在函数极值点为零矩阵。
   • 共轭梯度指向函数最陡增大斜率方向，负共轭梯度指向函数最陡下降斜率方向。
   • 最陡增大斜率的幅值为\(\| {\triangledown}_{\mathbf{Z}^{*}}f(\mathbf{Z},\mathbf{Z}^{*}) \|_{F}\)。
   • 共轭梯度是曲面\(f(\mathbf{Z},\mathbf{Z}^{*})=\mathrm{const}\)的法线。

4. 复Hessian矩阵：

   • 向量变元：定义全Hessian矩阵\(\mathbf{H}=\begin{bmatrix} \mathbf{H}_{\mathbf{z}^{*}, \mathbf{z}} & \mathbf{H}_{\mathbf{z}^{*}, \mathbf{z}^{*}} \\ \mathbf{H}_{\mathbf{z}, \mathbf{z}} & \mathbf{H}_{\mathbf{z}, \mathbf{z}^{*}} \end{bmatrix}\)，部分Hessian矩阵如下所示

     \[\mathbf{H}_{\mathbf{z}^{*}, \mathbf{z}}=\frac{\partial^{2} f(\mathbf{z}, \mathbf{z}^{*})}{\partial \mathbf{z}^{*} \partial\mathbf{z}^{T}} \\ \mathbf{H}_{\mathbf{z}^{*}, \mathbf{z}^{*}}=\frac{\partial^{2} f(\mathbf{z}, \mathbf{z}^{*})}{\partial \mathbf{z}^{*} \partial\mathbf{z}^{H}} \\ \mathbf{H}_{\mathbf{z}, \mathbf{z}}=\frac{\partial^{2} f(\mathbf{z}, \mathbf{z}^{*})}{\partial \mathbf{z} \partial\mathbf{z}^{T}} \\ \mathbf{H}_{\mathbf{z}, \mathbf{z}^{*}}=\frac{\partial^{2} f(\mathbf{z}, \mathbf{z}^{*})}{\partial \mathbf{z} \partial\mathbf{z}^{H}} \]

   • 矩阵变元：定义全Hessian矩阵\(\mathbf{H}=\begin{bmatrix} \mathbf{H}_{\mathbf{Z}^{*}, \mathbf{Z}} & \mathbf{H}_{\mathbf{Z}^{*}, \mathbf{Z}^{*}} \\ \mathbf{H}_{\mathbf{Z}, \mathbf{Z}} & \mathbf{H}_{\mathbf{Z}, \mathbf{Z}^{*}} \end{bmatrix}\)，部分Hessian矩阵如下所示

   \[\mathbf{H}_{\mathbf{Z}^{*}, \mathbf{Z}}=\frac{\partial^{2} f(\mathbf{Z}, \mathbf{Z}^{*})}{\partial \mathrm{vec} \mathbf{Z}^{*} \partial(\mathrm{vec} \mathbf{Z})^{\mathrm{T}}} \\ \mathbf{H}_{\mathbf{Z}^{*}, \mathbf{Z}^{*}}=\frac{\partial^{2} f(\mathbf{Z}, \mathbf{Z}^{*})}{\partial \mathrm{vec} \mathbf{Z}^{*} \partial(\mathrm{vec} \mathbf{Z}^{*})^{\mathrm{T}}} \\ \mathbf{H}_{\mathbf{Z}, \mathbf{Z}}=\frac{\partial^{2} f(\mathbf{Z}, \mathbf{Z}^{*})}{\partial \mathrm{vec} \mathbf{Z} \partial(\mathrm{vec} \mathbf{Z})^{\mathrm{T}}} \\ \mathbf{H}_{\mathbf{Z}, \mathbf{Z}^{*}}=\frac{\partial^{2} f(\mathbf{Z}, \mathbf{Z}^{*})}{\partial \mathrm{vec} \mathbf{Z} \partial(\mathrm{vec} \mathbf{Z}^{*})^{\mathrm{T}}} \]
   • 全Hessian矩阵为Hermitian矩阵。

5. 复Jacobi矩阵辨识：

   

6. 复Hessian矩阵辨识：有\(\mathrm{tr}(\mathbf{C}(\mathrm{d} \mathbf{Z}) \mathbf{D}(\mathrm{d} \mathbf{Z})^{\mathrm{T}}) \;\Leftrightarrow\; \mathbf{H}_{\mathbf{Z}, \mathbf{Z}}=\frac{1}{2}(\mathbf{D}^{\mathrm{T}} \otimes \mathbf{C}+\mathbf{D} \otimes \mathbf{C}^{\mathrm{T}})\)和 \(\mathrm{tr}(\mathbf{E}(\mathrm{d} \mathbf{Z}) \mathbf{F}(\mathrm{d} \mathbf{Z}^{*})^{\mathrm{T}}) \;\Leftrightarrow\; \mathbf{H}_{\mathbf{Z}, \mathbf{Z}^{*}}=\frac{1}{2}(\mathbf{F}^{\mathrm{T}} \otimes \mathbf{E}+\mathbf{F}^{*} \otimes \mathbf{E}^{\mathrm{H}})\)成立。