算法第五章作业以及课程小结
算法第五章作业及学期总结
- 对回溯算法的理解
我做了以下几道题,通过习题初步掌握了回溯算法的基本思考流程和代码实现方式,对于更难的回溯搜索问题,还需要进一步的学习
- 小猫爬山
题解
因为 \(n\) 很小,所以我们可以暴力枚举所有情况
那么,我们要考虑的问题是搜索的顺序,dfs函数的参数
- 搜索的顺序
对于每个小猫,我们有两种决策
- 如果当前已有的车不超重,把它放到当前已有的车中
for循环找已有的车
- 如果当前的车超重,把它放到新的车中
- 函数参数
对于参数,定义 \(dfs(int \ u ,\ int \ k)\) —保证了所有情况都可以被找到
\(u\) 表示当前枚举到第几只小猫
\(k\) 表示当前有几辆车
- 剪枝优化
- \(k \ge ans\) 时,当前分支继续往下走不能把 \(ans\) 变得更小
- (典型优化) 尽量让搜索树离根比较近位置的分叉少一些 \(\to\) 更早的减去递归搜索树的枝,即,优先考虑决策少的元素
- 对于本题而言,重量比较中的猫选择第二种方式的可能性大,重量比较轻的猫选择第一种的可能性大,而第一种由于要遍历 \(1\to k\) 比较耗时,所以从重量大的猫开始选更优
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
#define debug(a) cout << #a << " " << a << endl
const int maxn = 1e5 + 7;
const int N = 20, M = N * 2;
const int inf = 0x3f3f3f;
const long long mod = 1e9 + 7;
int n, w;
int sum[N], cat[N];
int ans = inf, k = 0;
void dfs(int u, int k) {
if(k >= ans) return ;
if(u > n) {
ans = k;
return ;
}
for(int i = 0; i < k; i++) {
if(sum[i] + cat[u] <= w) {
sum[i] += cat[u];
dfs(u + 1, k);
sum[i] -= cat[u];
}
}
sum[k] = cat[u];
dfs(u + 1, k + 1);
sum[k] = 0;
}
int main() {
#ifdef _DEBUG
// freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
ios::sync_with_stdio(false);
cin >> n >> w;
for(int i = 1; i <= n; i++) {
cin >> cat[i];
}
dfs(1, 0);
sort(cat + 1, cat + 1 + n);
reverse(cat + 1, cat + 1 + n);
cout << ans << '\n';
return 0;
}
- 排列数字
题意
给定一个整数\(n\),将数字\(1\to n\)排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
题解
- 根据题目,很容易构造出以每一个数字开始的解空间树,分别对从 \(1,2,3,4...n-1,n\)开始的数字进行全排列搜索
- 故
dfs定义:求出从第 \(u\) 行到最后一行的所有 \(path\) - 回溯的特征: 每一次都去现场找没被访问过的元素
Code
- 关于
dfs的代码基本思路
//子集型
void backtrack (int t) {
if (t > n) output(x);
else
for (int i = f(n, t); i <= g(n, t); i++) {
x[t] = h(i);
if (constraint(t) && bound(t)) backtrack(t + 1);
}
}
//排列型
void Swap(int *p, int *q) {
int temp;
temp = *p;
*p = *q;
*q = temp;
}
void Backtrack(int t) {
int i;
if(t > n) {
Output(x);
return;
}
for(i = t; i <= n; i++)
if(....) {
Swap(&x[t], &x[i]);
Backtrack(t + 1);
Swap(&x[t], &x[i]);//回溯
}
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 7;
const int N = 1010;
const int inf = 0x3f3f3f;
int n;
int path[N];
bool st[N];
void dfs(int u) {
if(u == n) {
for(int i = 0; i < n; i++) printf("%d ", path[i]);
puts("");
return;
}
//对于每一个数字开始进行搜索它的全排列
for(int i = 1; i <= n; i++) {
if(!st[i]) {
//更新状态
st[i] = true;
path[u] = i;
dfs(u + 1);
//恢复现场->回溯
st[i] = false;
path[u] = 0;
}
}
}
int main() {
scanf("%d", &n);
dfs(0);
return 0;
}
- n皇后
题意
题解
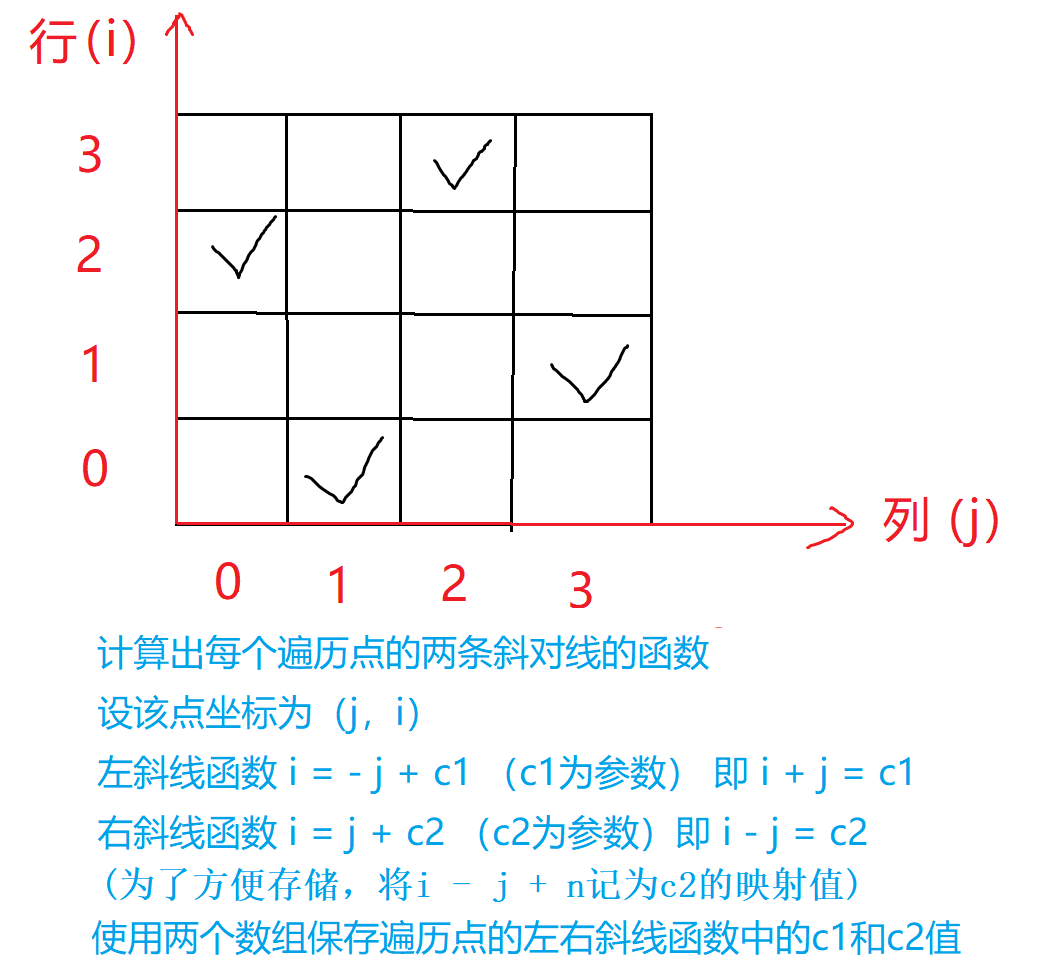
按行继续比遍历,其中\(col[x],dg[y - x + n],udg[x + y]\)分别记录的是该位置的列,斜,反斜线上是否已经存在过,若均不存在,填入皇后,并递归到下一行
对角线 \(dg[u+i]\),反对角线\(udg[n−u+i]\)中的下标 \(u+i\)和 \(n−u+i\)表示的是截距
下面的 \((x,y)\) 相当于\((u,i)\)
- 反对角线 \(y=x+b\) , 截距 \(b=y−x\) ,因为我们要把 \(b\) 当做数组下标,所以 \(b\) 不能是负的,所以我们 \(+n\) ,保证是结果是正的
- 而对角线 \(y=−x+b\) , 截距是 \(b=y+x\) ,这里截距一定是正的,所以不需要加偏移量
或者保证行号差和列号差不相等,即
Code
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行,故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts(""); // 换行
return;
}
//对n个位置按行搜索
for (int i = 0; i < n; i ++ )
// 剪枝(对于不满足要求的点,不再继续往下搜索) udg[n - u + i],+n是为了保证大于0
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
// 恢复现场 这步很关键
col[i] = dg[u + i] = udg[n - u + i] = false;
g[u][i] = '.';
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
- 树的最长路径
题解
- 树的最长路径 \(\to\) 树的直径
找树的直径的方法
-
任取一点作为起点,找出离该点距离最远的点 \(u\) DFS/BFS
-
再找到离 \(u\) 最远的一点 \(v\) DFS/BFS
那么, \(u,v\) 之间的路径就是树的直径
证明如下
证明的目标:第一个找到的 \(u\) 一定是某个直径的起点

- 分类
把这些树的直径分成若干类,使得分类唯一,在每一类中求最大值

- 现在,问题转化为,如何求挂到某点上的树的路径的长度最大值
设求结点 \(u\) 的路径长度最大值,可以求 \(v_1,v_2,v_3...v_n\) 这些子节点的长度的最大值
这样产生了以下两种方式

对于第一种情况:直接找子树路径的最大值
对于第二种情况:找子树路径的最大值和次大值,将他们相加就行了
找最大值和次大值的操作可以用循环实现
这种做法对于正负边权均适用
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
#define debug(a) cout << #a << " " << a << endl
const int maxn = 1e5 + 7;
const int N = 1e5 + 7, M = N * 2;
const int inf = 0x3f3f3f;
const long long mod = 1e9 + 7;
int e[M], ne[M], w[M], h[N], idx;
int ans;
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int dfs(int u, int father) {
int dist = 0;
int d1 = 0, d2 = 0;
for(int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if(v == father) continue;
int d = dfs(v, u) + w[i];
dist = max(dist, d);
if(d >= d1) d2 = d1, d1 = d;
else if(d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return dist;
}
int main() {
// ios::sync_with_stdio(false);
int n;
scanf("%d", &n);
memset(h, -1, sizeof(h));
for(int i = 1; i <= n - 1; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
dfs(1, -1);
printf("%d", ans);
return 0;
}
- 地下迷宫探索
描述
地道战是在抗日战争时期,在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事,如下图所示。
我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?
输入格式
输入第一行给出三个正整数,分别表示地下迷宫的节点数\(N(1<N≤1000,表示通道所有交叉点和端点)\)、边数\(M(≤3000,表示通道数)\)和探索起始节点编号\(S\)(节点从\(1\)到\(N\)编号)。随后的\(M\)行对应\(M\)条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出格式
若可以点亮所有节点的灯,则输出从S开始并以S结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
输入样例1
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
输出样例1
1 2 3 4 5 6 5 4 3 2 1
输入样例2
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
输出样例2
6 4 5 4 6 0
题意
略
题解
一道DFS的简单存储模板,注意进入和回溯的位置
关于图的存储可以参考:https://blog.csdn.net/Muyunuu/article/details/106675174
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 2e6 + 7;
struct edge {
int from, to, w;
edge(int a, int b, int c) {
from = a;
to = b;
w = c;
}
};
vector<edge> e[150000];
void init(int n) {
for (long long i = 0; i <= n; ++i) {
e[i].clear();
}
}
int vis[100000];
queue<int> path;
void DFS(vector<edge>(x[]), int s) {
vis[s] = 1;
path.push(s);//这里表示记录通过时的路径
for (long long i = 0; i < x[s].size(); ++i) {
int u = x[s][i].to;
if (!vis[u]) {
DFS(x, u);
path.push(s);//这里表示记录回溯时的路径
}
}
}
void debug(int n) {
for (long long i = 1; i <= n; ++i) {
cout << e[i][0].from << " ";
for (long long j = 0; j < e[i].size(); ++j) {
cout << e[i][j].to << " ";
}
cout << endl;
}
}
int main() {
int n, m, s;
cin >> n >> m >> s;
init(n);//初始化vector数组
for (long long i = 1; i <= m; ++i) {
int x, y;
cin >> x >> y;
e[x].push_back(edge(x, y, 1));
e[y].push_back(edge(y, x, 1));
}
for (long long i = 1; i <= n; ++i) {//冒泡排序,以符合题目的输出要求
for (long long j = 0; j < e[i].size() - 1; ++j) {
for (long long k = 0; k < e[i].size() - 1 - j; ++k) {
if (e[i][k].to > e[i][k + 1].to) swap(e[i][k].to, e[i][k + 1].to);
}
}
}
//debug(n);
DFS(e, s);
//检查有没有所有节点是否都被访问到
int flag = 0;
for (long long i = 1; i <= n; ++i) {
if (!vis[i]) {
flag = 1;
break;
}
}
//输出路径
while (!path.empty()) {
if (path.size() == 1) {
cout << path.front();
break;
}
cout << path.front() << " ";
path.pop();
}
if (flag) cout << " " << 0;
return 0;
}
- 学习算法课程收获
初步认识了 \(dp\) \(dfs\) \(bfs\) 等常用算法,对计算机科学的兴趣更浓了
- 学习中遇到的困难
自己检索里面过于困难,希望提供更加多更加具体分类的算法在线测评题库
- 课程的教学建议
希望能够多收集一些题目,按章节建成一些分类题集(大约每章节20题)放在OJ上



 浙公网安备 33010602011771号
浙公网安备 33010602011771号